
Пифагор и зарождение математики
- О жизни Пифагора известно только то, что ничего нельзя утверждать наверняка. О нём было написано много и мало.
Автор: ученица 9 класса Кулябовского филиала МБОУ Мучкапской СОШ Колядиной Кристины.
Преподаватель: Кузнецова Надежда Петровна.


Биография Пифагора
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосее. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора не известно

В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас

Пифагорейцами было сделано много важных открытей в арифметике и геометрии, в том числе:
- Теорема о сумме внутренних углов треугольника;
- Построение правильных многоугольников и деление плоскости на некоторых из них,
- Геометрические способы решения квадратных уравнений;
- Деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
- Доказательство того, что корень из 2 не является рациональным числом;
- Создании математической теории музыки и учения об арифметических, геометрических гармонических пропорциях и многое другое.

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна.

Теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций .

Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокол, комментируя последнее предложение первой книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принес в жертву быка». Впрочем, более щедрые сказители одного быка превратили в одну гекатомбу, а это уже целая сотня. И хотя еще Цицерон заметил, что всякое пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие отклики.

Так, оптимист Михаил Ломоносов (1711--1765) писал: «Пифагор за изобретение одного геометрического правила Зевсу принес на жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось».

Генрих Гейне (1797—1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принес в жертву бессмертным богам».

...Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.

" Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах."

Способы доказательство теоремы Пифагора
Не алгебраические доказательства теоремы.
А) Простейшее доказательство.
Б) Древнекитайское доказательство.
В) Древнеиндийское доказательство.
Г) Доказательство Евклида.

Простейшее доказательство
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников чтобы убедиться в справедливости теоремы. Например, для ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.
доказательству Рис. 2
подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+ b , а внутренний — квадрат со стороной с, построенный на гипотенузе (рис. 2, б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. 2, в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис. 2, а), не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (рис. 2, б) отрезать и приложить гипотенузами к двум другим гипотенузам (рис. 2, г), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b , т.е. с2=а2+Ь2.
Древнекитайское доказательство
Рис. 2

На рисунке воспроизведен чертеж из трактата «Чжоу-би...». Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете—16. Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете.

Древнеиндийское доказательство
- Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж (рис. а) с характерным для индийских доказательств словом «смотри!». Как видим, прямо-угольньные треугольники уложены здесь гипотенузой наружу и квадрат с 2 перекладывается в «кресло невесты» а2- b 2 (рис. б). Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше площади данного квадрата) встречаются в древнеиндийском трактате «Сульва сутра» (VII —V вв. до н.э.).
Рис. 4
Доказательство Евклида
Доказательство Евклида приведено в предложении 47 первой книги «Начал». На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH , а прямоугольник ICEL — квадрату АС КС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе. В самом деле, затушеванные на рисунке треугольники ABD и BFC равны по двум сторонам и углу между ними: FB = AB , BC == BD и FBC = d + ABC = ABD . Но SABD =1/2 SBJLD , так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD . Аналогично SFBC = 1\2 SABFH ( BF — общее основание, АВ— общая высота). Отсюда, учитывая, что SABD = SFBC , имеем SBJLD = SABFH . Аналогично, используя равенство треугольников ВСК. и АСЕ, доказывается, что SJCEL = SACKG . Итак, SABFH + SACKG = SBJLD + SJCEL = SBCED , что и требовалось доказать. Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой причине его нередко называли «ходульным» и «надуманным». Но такое мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном в цепи предложений 1-й книги «Начал». Для того чтобы логически безупречно построить эту цепь, чтобы каждый шаг доказательства был основан на ранее доказанных предложениях, Евклиду нужен был именно выбранный им путь.
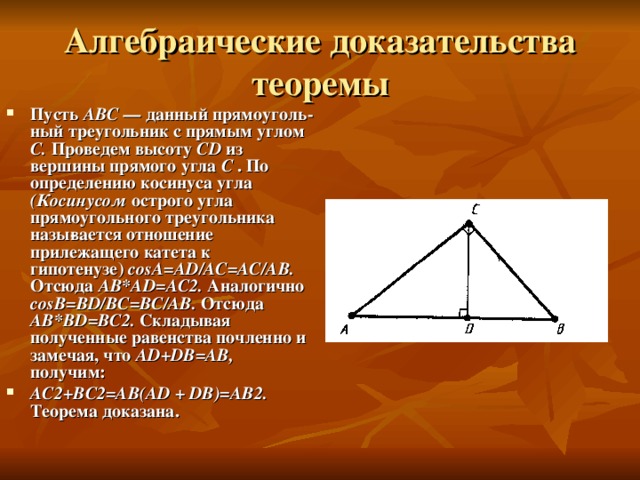
Алгебраические доказательства теоремы
- Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С . По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) со s А= AD / AC = AC / AB . Отсюда AB * AD = AC 2. Аналогично со s В= BD / BC = BC / AB . Отсюда AB * BD =ВС2. Складывая полученные равенства почленно и замечая, что AD + DB = AB , получим:
- АС2+ВС2=АВ( AD + DB )=АВ2. Теорема доказана.



 Получите свидетельство
Получите свидетельство Вход
Вход



































 Великие математики (3.23 MB)
Великие математики (3.23 MB)
 0
0 508
508 16
16 Нравится
0
Нравится
0



