Векторное произведение векторов

Векторное

произведение

векторов

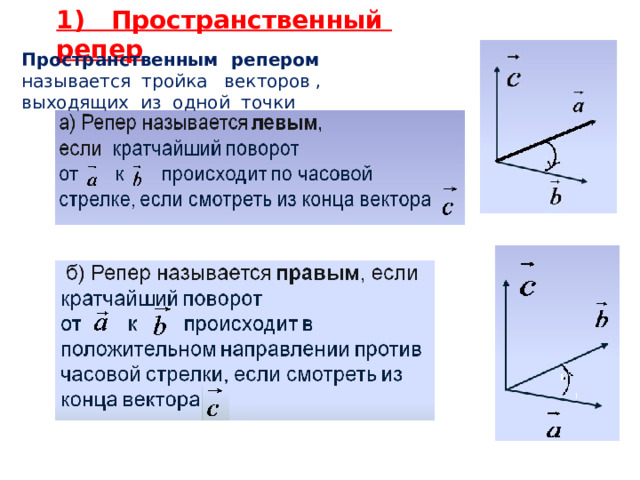
1) Пространственный репер

Пространственным репером называется тройка векторов , выходящих из одной точки

2) Понятие векторного произведения

обозначение

3) Свойства векторного произведения

№ 1 Упростить

№ 2: Упростите выражение

Ответ:

4) ВЫЧИСЛЕНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ

Пусть вектора заданы своими координатами

тогда координаты векторного произведения вычисляются по формуле

№ 3. Вычислить

Задание:

№ 4 Даны векторы a(-1;2;3), b(4;2;0)

Вычислите [ba]

• Ответ: [ba] =(6; -12; 10)

№ 5 Даны векторы с(0;1;5), b(1;-3;2)

Вычислите [сb]

Ответ: [сb] =(17; 5; -1)

5) Следствие из векторного произведения

Пример:

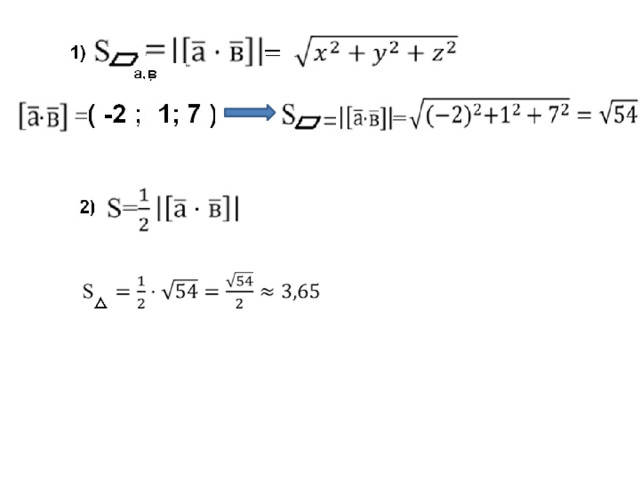
Задание:

Даны векторы a(1;0;5), b(2;-2;1)

Вычислите:

1) векторное произведение [ab]

2) Площадь параллелограмма, построенного на векторах a и b

3) Площадь треугольника, построенного на векторах a и b

4) Синус угла между векторами a и b

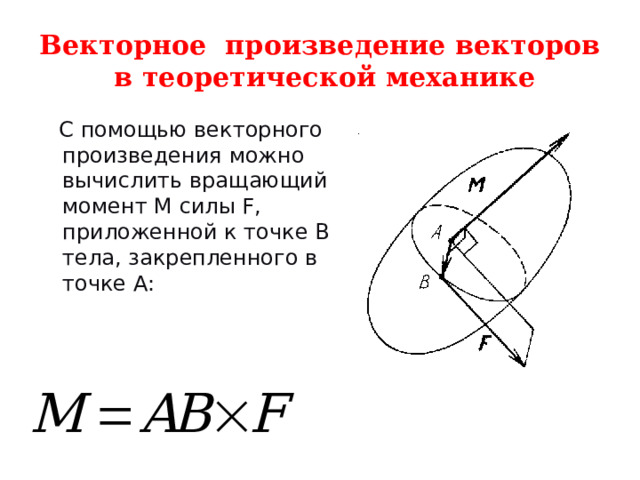
Векторное произведение векторов в теоретической механике

С помощью векторного произведения можно вычислить вращающий момент М силы F, приложенной к точке В тела, закрепленного в точке А: