Вертикальные углы

Презентация из 15 слайдов содержит определение, обозначение, свойства вертикальных углов.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Теорема Вертикальные углы равны. - Доказательство в презентации.

Задача №1

Любые два угла, которые получаются при пересечении двух прямых, либо смежные, либо вертикальные.

Задача 2

Один из углов, образовавшихся при пересечении двух прямых равен 36°. Найти остальные углы.

Задача 3

Разность двух углов, получившихся при пересечении двух прямых равна 50°. Найти эти углы.

Два угла, которые получаются при пересечении двух прямых, - либо смежные, либо вертикальные углы.

Данные по условию углы не могут быть вертикальными, так как они не равны: их разность равна 50°, значит, они  - смежные.

Задача 4

Сумма двух углов, получившихся при пересечении двух прямых равна 80°. Найти все углы.

ВЕРТИКАЛЬНЫЕ УГЛЫ

Определение,

обозначение,

свойства.

Учитель Козина Н.А.

ВЕРТИКАЛЬНЫЕ УГЛЫ

Определение

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

ВЕРТИКАЛЬНЫЕ УГЛЫ

Определение

B

C

M

A

D

•  AMB и  CMD – вертикальные;

• BA и BD; BC и BM – являются продолжениями сторон другого.

•  BMC и  AMD – вертикальные;

ВЕРТИКАЛЬНЫЕ УГЛЫ

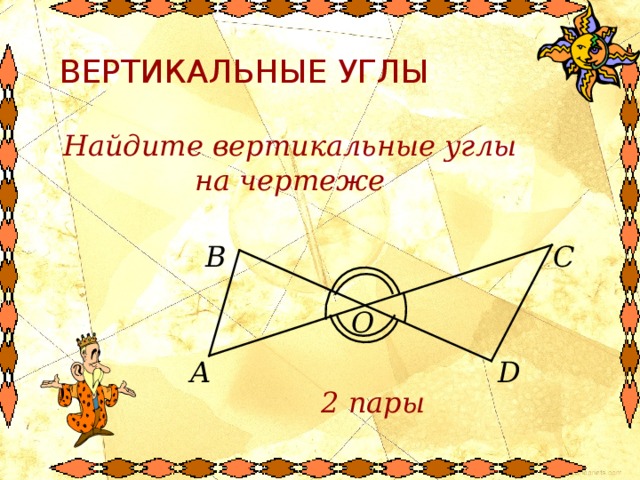
Найдите вертикальные углы на чертеже

C

B

O

A

D

2 пары

ВЕРТИКАЛЬНЫЕ УГЛЫ

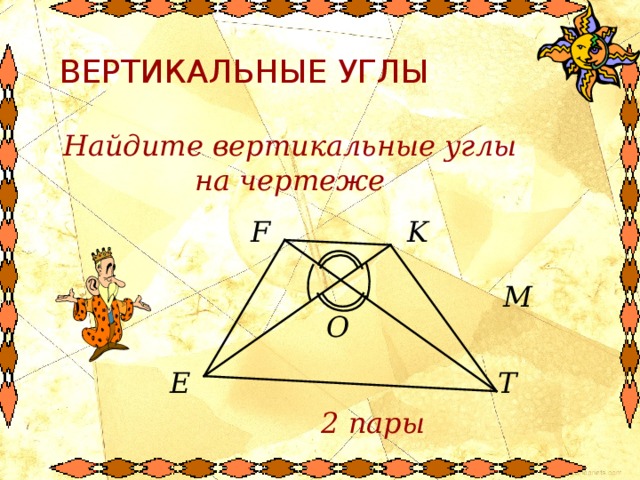
Найдите вертикальные углы на чертеже

K

F

M

О

E

T

2 пары

ТЕОРЕМА 2.2

Вертикальные углы равны.

C

B



• Дано:  AOB и  COD – вертикальные.
• Доказать:  AOB =  COD .

O

A

D

Доказательство

•  AOB и  BOC – смежные по определению;
•  AOB +  BOC = 180 ° по свойству смежных углов .

• Пусть  BOC =  , тогда  AOB = 180 ° -  .

ТЕОРЕМА 2.2

C

B



• Дано:  AOB и  COD – вертикальные.
• Доказать:  AOB =  COD .

O

A

D

Доказательство

• Пусть  BOC =  , тогда  AOB = 180 ° -  .

•  BOC и  COD – смежные по определению;
•  BOC +  COD = 180 ° по свойству смежных углов .
•  COD = 180 ° - 
•  AOB =  COD .

ЗАДАЧА №1

Любые два угла, которые получаются при пересечении двух прямых, либо смежные, либо вертикальные.

 1 и  2 – смежные

 1 и  3 – вертикальные

 1 и  4 – смежные

 2 и  3 –смежные

 2 и  4 – вертикальные

 3 и  4 – смежные

2

1

3

4

Запомнить!

ЗАДАЧА №2

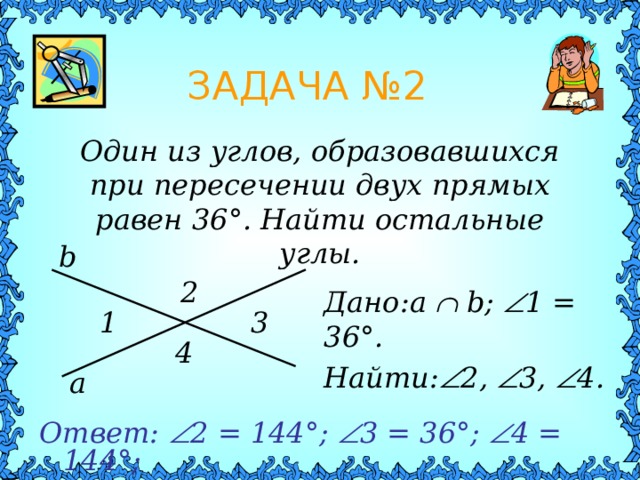
Один из углов, образовавшихся при пересечении двух прямых равен 36 ° . Найти остальные углы.

b

2

Дано: a  b;  1 = 36 °.

Найти:  2 ,  3 ,  4 .

1

3

4

a

Ответ:  2 = 144 °;  3 = 36°;  4 = 144 °;

ЗАДАЧА № 3

Разность двух углов, получившихся при пересечении двух прямых равна 50 ° . Найти эти углы.

• Два угла, которые получаются при пересечении двух прямых, - либо смежные, либо вертикальные углы.
• Данные по условию углы не могут быть вертикальными, так как они не равны: их разность равна 50 ° , значит, они - смежные.

b

Разность двух углов, получившихся при пересечении двух прямых равна 50 ° . Найти эти углы.

2

1

a

Дано: a  b;  1 и  2 – смежные ;

 1 ? на 50 ° меньше

 2 ?

Найти:  1 ,  2 .

x °

(x + 50)°

Ответ:  1 = 115 °;  2 = 6 5 ° .

ЗАДАЧА № 4

Сумма двух углов, получившихся при пересечении двух прямых равна 80 ° . Найти все углы.

• Два угла, которые получаются при пересечении двух прямых, - либо смежные, либо вертикальные углы.
• Сумма смежных углов равна 180 ° , значит, по условию даны вертикальные углы, т.к. их сумма равна 80 ° .

b

Сумма двух углов, получившихся при пересечении двух прямых равна 80 ° . Найти все углы.

2

1

3

4

a

Дано: a  b;  1 и  3 – вертикальные

 1 +  3 = 80 °

Найти:  1 ,  2,  3 ,  4 .

Ответ:  1 =  3 = 40 °;

 2 =  4 = 140 ° .

ДОМАШНЕЕ ЗАДАНИЕ

Учебник. П15.

Вопросы 6,7.

Задачи №7, №9.

Рабочая тетрадь №90; №91; №92.