Вариант ЕГЭ по геометрии 10 класс

Вариант

1.  Найдите площадь квадрата, вершины которого имеют координаты (3; 1), (10; 1), (10; 8), (3; 8).

2. 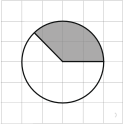 На клетчатой бумаге с размером клетки   изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

3. 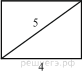 Найдите площадь прямоугольника по данным рисунка.

4.

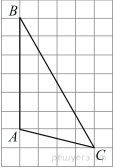
На клетчатой бумаге с размером клетки 1х1 изображён треугольник   Найдите длину его средней линии, параллельной стороне 

5.

Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1×1 см. Ответ дайте в квадратных сантиметрах.

6. 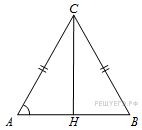 В треугольнике ABC AC = BC, AB = 22,   Найдите AC.

7. Площадь треугольника равна 14, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.

8. 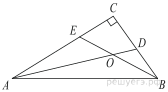 Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

9. 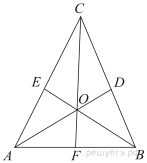 В треугольнике ABC угол A равен  , угол B равен   AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

10. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

.

11. 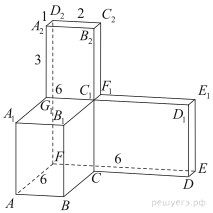 Найдите угол   многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

12. В прямоугольном параллелепипеде   ребро  , ребро  , ребро   Точка   — середина ребра   Найдите площадь сечения, проходящего через точки   и 

.

13.  Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

14. В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A₁C₁.

а) Постройте сечение призмы плоскостью BAN.

б) Найдите периметр этого сечения.

15. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.

а) Докажите, что треугольник ABC равнобедренный.

б) Найдите, в каком отношении высота этого треугольника делит сторону BC.