Тема: Решение систем уравнений второй степени с двумя переменными. Графический способ.
Цели урока:
образовательные:
систематизировать понятие системы уравнений с двумя переменными, ее решения;
рассмотреть графический способ решения системы уравнений;
закрепить навыки построения графиков функций;
развивающие:
развивать логическое мышление, математическую речь, вычислительные навыки;
развивать умение применять полученные знания к решению прикладных задач;
расширение кругозора;
воспитывающие:
воспитание познавательного интереса к предмету.
Ход урока.
1. Орг. момент
Добрый день! Добрый час!
Как я рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись. Подровнялись.
Друг на друга поглядели
И тихонько дружно сели.
2. Мотивация урока.
Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя.
3. Актуализация опорных знаний. Проверка д/з.
Какие функции нам знакомы из курса алгебры 7-9 классов?
Линейная. Прямая и обратная пропорциональность. Квадратичная функция.
Для повторения используется материал учебника -пп. 31-37.
Графики функций. Уравнение окружности.
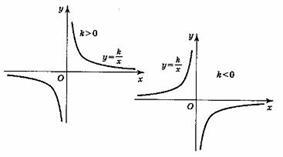
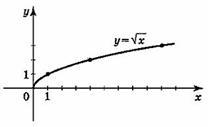
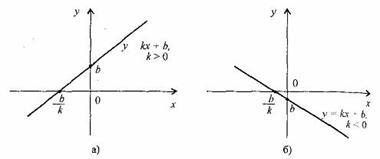
График уравнения с двумя переменными.
Вы знаете, что иллюстрацией уравнений служат их графики на координатной плоскости. Работа с таблицей. (Ученики работают в рабочих картах урока.)
| Уравнение | Степень | Выражаем у через х | Данной формулой задается … функция | Графиком является … |
| 3х+2у=6 |
|
|
|
|
| у-х2=0 |
|
|
|
|
| 2х+у=0 |
|
|
|
|
| ху=4 |
|
|
|
|
Графики уравнений с 2 переменными весьма разнообразны.
Обратите внимание на таблицу:
Если уравнение - первой степени, график всегда - прямая.
Если второй степени, то получается гипербола или парабола.
А если обе переменные входят в уравнение во второй степени, то какую линию имеем? Ответ учащихся: уравнение окружности.
4. Изучение нового материала.
Что такое система уравнений?
Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой.
- Что является решением системы уравнений с двумя переменными? (пара значений переменных, обращающая каждое уравнение системы в верное равенство).
- Является ли пара чисел (2;3) решением системы
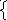
х+2у=8,
5х-2у=4
- Какие способы решения систем уравнений вы знаете?
Какой способ решения изображен на рисунке? (Графический)
Вспомним алгоритм решения систем уравнений графическим способом:
1)Выразить в каждом уравнении у через переменную х,
2)Построить в одной системе координат графики полученных функций,
3)Рассмотреть взаимное расположение графиков.
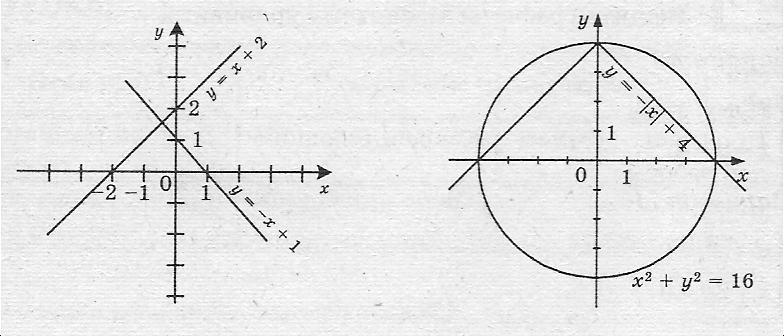
* Сколько решений может иметь система линейных уравнений с двумя переменными?
одно, если прямые пересекаются;
если прямые параллельны, то нет решения;
Если прямые совпадают, то бесконечное множество решений.
План решения системы уравнений графическим способом
Выразить переменную у в первом уравнении.
Выразить переменную у во втором уравнении.
В одной системе построить графики данных функций.
Координаты точки пересечения графиков и является решением системы уравнений.
Но, к сожалению, графический способ не всегда обеспечивает высокую точность результата, не всегда решения являются точными. В основном этот метод применяется для:
* нахождения приближенных решений;
* с помощью этого метода легко выяснить, сколько решений может иметь система уравнений.
Чтобы проверить точность полученных решений, их нужно подставить в уравнения системы!
- Ребята, как определяется степень целого уравнения с одной переменной? (Если уравнение с одной переменной записано в виде Р(х) = 0, где Р(х) - многочлен стандартного вида, то степень этого многочлена называют степенью уравнения) .
Степень целого уравнения с двумя переменными определяется аналогично. Чтобы выяснить, какова степень какого-либо уравнения с двумя переменными, его заменяют равносильным уравнением, левая часть которого- многочлен стандартного вида, а правая - нуль.
На рисунке изображены графики функций
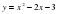 и
и 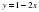 .
.
Используя график, решите систему уравнений
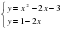
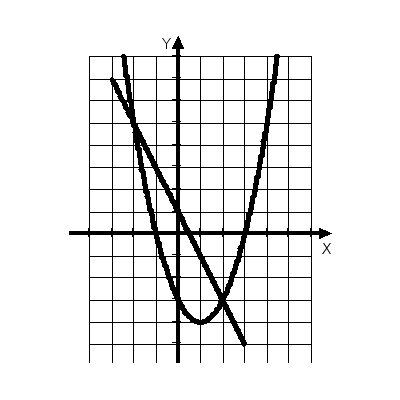
1
0
2) Решить систему уравнений графическим способом по алгоритму:
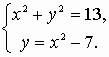
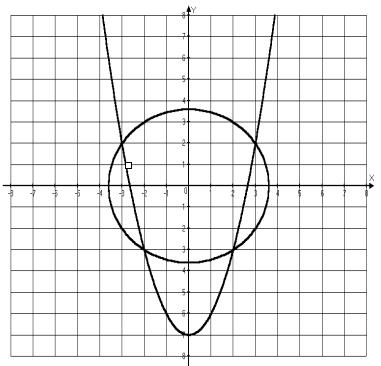
5. Физкультминутка
1.Мы зарядку начинаем,
Наши руки разминаем,
Разминаем спину, плечи,
Чтоб сидеть нам было легче
2.Крутим-вертим головой.
Разминаем шею, стой!
Раз, два, три – наклон направо,
Раз, два, три - теперь налево.
3.А теперь остановись!
Поднимаем руки выше,
Вдох и выдох. Глубже дышим.
А теперь за парты сядем.
6. Закрепление нового материала.
Решить №444(1-3), 448(3, 4).
7. Самостоятельная работа.
Тест
1. Определить уравнения второй степени:
а) ху – 2у = 5; б) х3 – у = 3; в) х2 + 3у2 =0
Ответы: 1) а; 2) б, в; 3) в; 4) а, в
2. Пара чисел (1; 0) является решением уравнения:
а) х2 + у = 1; б) ху + 3 = х; в) у ( х + 2 ) =0
Ответы: 1) а; 2) б, в; 3) в; 4) а, в
3. Уравнение окружности:
а) х2 + у2 = 4; б) (х –у)2 + (у + 3)2 = 9; в) х2 + (3 –у)2 =4
Ответы: 1) а, б; 2) б, в; 3) в; 4) а, в,
4.Решением системы уравнений ху + 4 = 0;
у = ( х – 1 )2, является:
Ответы: 1) (1;4); 2) (1;-4); 3) (-1;-4); 4) (-1;4)
Ответы к тесту ( 1) 4; 2) 4; 3) 4; 4) 4.)
Задания для повторения (из курса «Математика 5-6 классы»)
Как называется операция, когда числитель и знаменатель дроби делят на одно и тоже число? (Сокращение)
Как называется множитель при делении общего знаменателя на знаменатель дроби? (Дополнительный множитель)
Какое число никогда не может быть знаменателем дроби? (ноль)
Как называется величина, которая показывает, насколько частей разделена одна целая? (знаменатель)
Как называется величина, которая показывает, сколько взято таких частей? (числитель)
Какую величину можно рассматривать, как частное от деления? (дробь)
Как разделить две обыкновенные дроби?
Устная работа: назовите число, обратное данному числу.
Разделите число в квадрате на каждое из чисел в кружках:
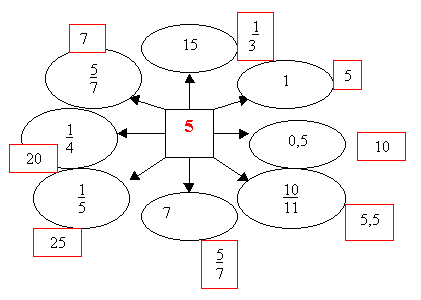
7. Подведение итогов урока. Рефлексия. Д/з.
1) Составление кластера. Ребята, давайте повторим алгоритм решения систем уравнений второй степени с двумя переменными.
2) Сравните 2 темы: решение систем линейных уравнений с двумя переменными и решение систем нелинейных уравнений с двумя переменными.
Что общего? (алгоритм решения).
Есть различие? (число решений)
Выучить п.13. Решить №445, 449(1,2).
Тема: Система уравнений с двумя переменными. Способ подстановки.
Цели урока:
образовательные:
закрепить графический способ и способ подстановки решения системы уравнений;
закрепить навыки построения графиков функций;
развивающие:
развивать логическое мышление, математическую речь, вычислительные навыки;
развивать умение применять полученные знания к решению прикладных задач;
расширение кругозора;
воспитывающие:
воспитание познавательного интереса к предмету.
Ход урока.
1. Орг. момент
Чтобы легче всем жилось,
Чтоб решалось, чтоб моглось.
Улыбнись, удача всем,
Чтобы не было проблем.
Улыбнулись, ребята, друг другу, создали хорошее настроение и начали работу.
2. Мотивация урока.
Сегодняшний урок я хотела начать с философской загадки Вальтера: Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и краткое, самое дорогое, но и дёшево ценимое нами? (время).
Итак, у нас всего 45 минут и мне очень хотелось, чтобы это время пролетело для вас незаметно и с пользой.
3. Актуализация опорных знаний. Проверка д/з.
Теоретическая разминка.
(повторение необходимых теоретических сведений по теме, развитие умений говорить и слушать, работа проходит устно).
1. Что называется решением системы двух уравнений с двумя
переменными?
2. Что значит решить систему уравнений?
3. Сколько решений может иметь система двух уравнений с двумя
переменными, если она содержит уравнение второй степени?
4. Какие существуют способы решения систем уравнений.
5. Повторите план решения системы графическим способом.
Устные задания:
1. Является ли пара чисел (1;0) решением уравнения:
а) x² + y = 1, б) xy +3 = x, в) y(x + 2) = 0.
2. Выразите переменную y через x
а) 5x + y = 7, б) x – y = 2, в) 2x – 2y = 8.
3. Что является графиком уравнения?
а) y =3x + 1;
б) y = 3;
в) y - x² = 2
г) x² + (y – 2)² = 4.
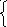 4. Имеет ли решения система уравнений?
4. Имеет ли решения система уравнений?
а) x² + у² = -5,
5x + 2у = 13.
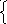 б) x + y = 2,
б) x + y = 2,
y = x² - 1.
Для каждого графика выберите формулу, которой задается соответствующая функция
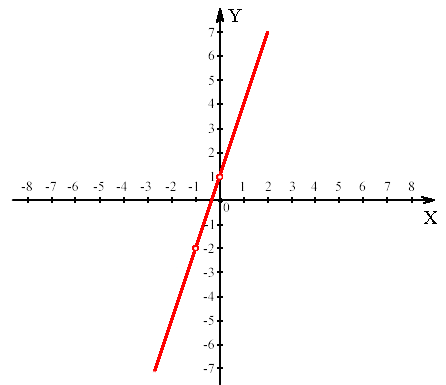
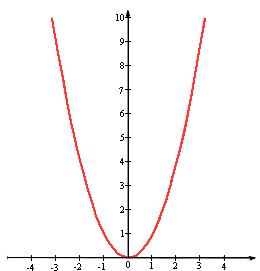
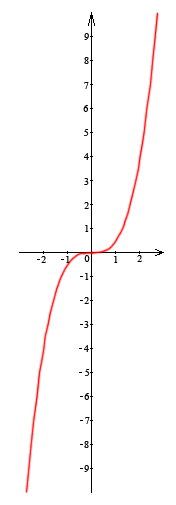
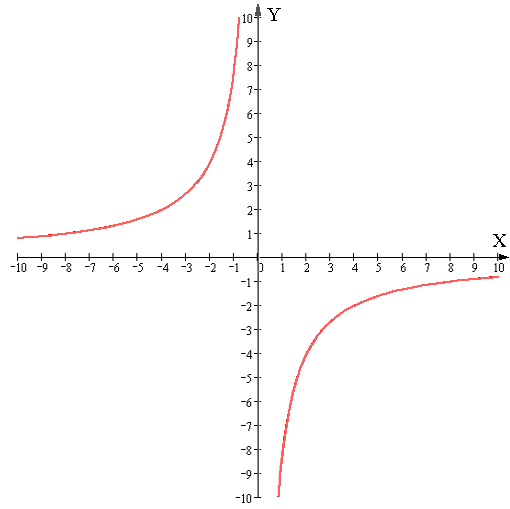
1. 2 3 4
А. у =3х+1. Б. у= - 8/х В. у= х2 Г. у= 0,5х 3
| 1. | 2. | 3. | 4. |
|
|
|
|
|
Сверка решения д/з №445(3) с доской.
Решить № 448(2).
Решить систему линейных уравнений способом подстановки:
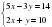

1.
 2. y = 10 – 2x
2. y = 10 – 2x
3. 5х – 3 (10 – 2х)=14
4. 5х – 30 + 6х = 14
11х = 44

х = 4
5. у = 10 – 2· 4
6. у = 2
7. (4; 2)
4. Изучение нового материала.
Алгоритм решения методом подстановки.
Выразить у через х (х через у) из первого уравнения системы.
Подставить полученное на первом шаге выражение вместо у во второе уравнение системы.
Решить полученное на втором шаге уравнение относительно х.
Подставить найденное на третьем шаге значение х в выражение у через х, полученное на первом шаге.
Записать ответ в виде пары значений (х;у), которые были найдены соответственно на третьем и четвёртом шагах.)
Решить систему уравнений способом подстановки по алгоритму:
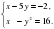 .
.
Выразим в уравнении первой степени х-5у=-2 одну переменную через другую х=-2+5у.
Подставим полученное выражение (-2+5у) в уравнение второй степени
(-2+5у)-у2=16.
Приведем уравнение к уравнению с одной переменной
-2+5у-у2=-16, -у2+5у-2+16=0, -у2+5у+14=0 ·(-1), у2-5у-14=0.
Решим квадратное уравнение
у2-5у-14=0, а=1; в=-5; с=-14, D=в2-4ас=(-5)2-4·1·(-14)=25+56=81=920 – два корня.
У1;2=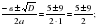 У1=
У1= У2=
Найдем значение второй переменной
Если У1=7, то х1=-2+5·7=33;
Если У2= -2, то х2=-2+5·(-2)=-2-10=-12.
(33;7); (-12; -2) – решения системы
Ответ: (33;7); (-12; -2).
Дополнительно:
x² + 2у = 6,
у = x – 1.
5. Динамическая пауза. ( Направлена на профилактику остеохондроза.)
Сесть на краешек стула.
Поднять руки, потянуться, напрячь мышцы.
Вытянуть руки перед грудью, потянуться.
Руки в стороны, потянуться, напрячь мышцы.
Обхватить себя руками, выгнуть спину.
Принять рабочее положение.
6. Закрепление нового материала.
Решить № 446, 450(1).
7. Самостоятельная работа.
Решить в парах № 450(4).
Задания для повторения (из курса «Математика 5-6 классы»)
Вспоминаем формулы (фронтальный опрос):
7. Подведение итогов урока. Рефлексия. Д/з.
Продолжи предложение
Сегодня на уроке я научился…
Сегодня на уроке мне понравилось…
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…
Сегодня на уроке я поставил себе оценку …
Какие виды работ вызвали затруднения и требуют повторения…
В каких знаниях уверен…
Помог ли урок продвинуться в знаниях, умениях, навыках по предмету…
Кому, над, чем следовало бы ещё поработать…
Насколько результативным был урок сегодня…
Выучить п.13. Решить № 447, 451(3).
Тема: Решение задач составлением систем уравнений с двумя переменными.
Цели урока:
познакомить учащихся с применением систем уравнений второй степени при решении задач; обеспечить овладение основными алгоритмическими приемами применения систем уравнений при решении задач; формирование умения переносить знания в новую ситуацию;
развивать логическое мышление, математическую речь, вычислительные навыки;
формирование умения работать в группе.
Ход урока.
1. Организационный момент.
Здравствуйте, друзья! Садитесь.
Мы урок наш начинаем,
Всем удачи пожелаем.
Вы друг друга поддержите
Постарайтесь, не ленитесь.
На 12 лишь трудитесь.
А дежурных прошу встать,
Кто отсутствует сказать.
2. Мотивация урока.
Математика много дает для умственного развития человека – заставляет думать, соображать, искать простые и красивые решения, помогает развивать логическое мышление, умение правильно и последовательно рассуждать, тренирует помять, внимание, закаляет характер. Надеюсь, что сегодня вы все будете работать с большим желанием узнать, что-то новое и в тоже время закрепить свои прошлые знания. Ведь как гласит народная мудрость: «Была бы охота – заладится всякая работа».
3. Актуализация опорных знаний. Проверка д/з.
Устный опрос:
| Сформулируйте теорему Пифагора | |
| Назовите формулы площади и периметра прямоугольника со сторонам a и b. | |
| Назовите формулы площади и периметра квадрата со стороной а | |
| Какие способы решения систем уравнений вам известны? | Способ подстановки. Способ сложения. |
Математический диктант.
Составьте уравнение с двумя переменными, если:
Сумма двух натуральных чисел равна 16.
Периметр прямоугольника равен 12 см.
Одна сторона прямоугольника на 8 см больше другой.
Произведение двух натуральных чисел равно 28.
Диагональ прямоугольника равна 5 см.
Решить № 454(1, 2).
4. Изучение нового материала.
-Где же применяются системы уравнений? Сегодня мы начнем рассматривать задачи, решить которые можно с помощью систем уравнений второй степени с двумя переменными.
Этапы решения задач:
1. Составление математической модели (система уравнений).
2. Работа с составленной моделью.
3. Ответ на вопрос задачи.
Задача. Диагональ прямоугольника равна 10см, а его периметр равен 28 см. Найдите стороны прямоугольника.
Что нам неизвестно?
Как обозначим эти неизвестные величины?
Как найти периметр нашего прямоугольника?
Составьте 1 уравнение системы: 2(х+у)=28
Как нам связать стороны с диагональю?
По теореме Пифагора получаем х2+у2=102 это второе уравнение системы
х+у=14
Х2+у2=100
Ответ: 6 и 8 см.
Схема решения задач
Анализ условия
Выделения двух ситуаций
Введение неизвестных
Установление зависимости между данными задачи и неизвестными
Составление уравнений
Решение системы уравнений
Запись ответа
5.Закрепление нового материала.
Решить № 479, 481.
6. Физкультминутка.
Провести физкультминутку, применив математическую считалочку:
« Один, два - не собьюсь,
Четыре, пять – не собьюсь,
Семь, восемь – не собьюсь,
Десять, одиннадцать – не собьюсь,
Тринадцать, четырнадцать – не собьюсь,
Шестнадцать, семнадцать – не собьюсь,
Девятнадцать, двадцать – не собьюсь»
7. Самостоятельная работа.
Решить № 477.
Задания для повторения (из курса «Математика 5-6 классы»)
Выполни тест и угадай слово.
1. 5, 76*100 =…
М) 576; К) 57, 6; А) 5,76; Т) свой ответ.
2. Произведение чисел 3,8 и 15 равно:
О) 57; М) 570; Н) 5,70; А) свой ответ.
3. Произведение чисел 0,735 и 1 равно:
О) 1; Д) 0; Л) 0,735; Ц) свой ответ.
4. Если первый множитель 1,9, а второй множитель 2,1, то произведение равно:
М) 399; Д) 39,9 О) 3,99; Ц) свой ответ.
5. Произведение чисел 2,5 и 0,4 равно:
М) 10; Н) 0,1; Д) 1; Ц) свой ответ.
6. Корень уравнения Х : 0,04=2,4 равен:
М) 2,44; Д) 0,96 Е) 0,096; Ц) свой ответ.
7.Если длина комнаты 7,6 м, а ширина 5,4 м, то ее площадь равна:
М) 41,04 м; Ц) 41,04 м²; О) 26 м²; Д) свой ответ.
Вот и получили слово: МОЛОДЕЦ!
8. Подведение итогов урока.
Рефлексия:
Рефлексия.
Оцени себя и сделай для себя вывод о пользе проведенного на уроке времени.
Оцените урок. На полях в конце записей поставьте оценку.
Я доволен уроком, мне очень понравилось, я всё понял(а).
Мне понравился урок, но в моих знаниях есть пробелы.
Я не доволен уроком, ничего не понял(а) и как решать, я не знаю.
9. Домашнее задание.
Выучить п.14.
Решить № 478, 480, 482.
Тема: Решение текстовых задач составлением систем уравнений с двумя переменными.
Цели урока:
закрепить умения учащихся решать текстовые задачи составлением систем уравнений второй степени с двумя переменными;
развивать логическое мышление, математическую речь, вычислительные навыки;
формирование умения работать в группе.
Ход урока.
1. Организационный момент.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В математики мир отправимся смело,
В мир примеров и разных задач.
А девизом нашего урока буду такие слова:
Думать - коллективно!
Решать - оперативно!
Отвечать - доказательно!
Бороться - старательно!
И открытия нас ждут обязательно!
2. Мотивация урока.
Историческая справка:
Уже около 4000 лет назад вавилоняне решали разные задачи землемерия, строительства и военного дела с помощью уравнений первой и второй степени. Уравнения тех же степеней умели решать в древности также китайские и индийские ученые. Задачи, решаемые с помощью уравнений, встречаются во многих текстах глубокой древности. В Московском папирусе и в папирусе Ахмеса, например, содержатся задачи, в которых неизвестное имеет особый символ
и название: «хау» или «аха». Оно означает «количество», «куча». Так называемое «исчисление кучи», или «вычисление хау» приблизительно соответствует нашему решению задач с помощью уравнений.
Какие способы решения систем уравнений вы знаете?
3. Актуализация опорных знаний. Проверка д/з ( сверка с доской № 478, 489).
Самостоятельная работа:
1 вариант
Разность двух чисел равна 5, а их произведение равно 84. Найдите эти числа.
Гипотенуза прямоугольного треугольника равна 13. Найдите его катеты, если известно, что один из них на 7 см больше другого
2 вариант
Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.
Гипотенуза прямоугольного треугольника равна 20. Найдите его катеты, если известно, что один из них на 4 см меньше другого
4. Решение текстовых задач составлением систем уравнений с двумя переменными.
Решить № 483, 490, 493.
5. Релаксационная пауза.
Закройте глаза, расслабьте тело,
Представьте – вы птицы, вы вдруг полетели!
Теперь в океане дельфином плывете,
Теперь в саду яблоки спелые рвете.
Налево, направо, вокруг посмотрели,
Открыли глаза, и снова за дело!
7. Самостоятельная работа.
Задания для повторения (из курса «Математика 5-6 классы»)
А теперь разгадайте ребус
Слово "пропорция" означает " соразмерные, имеющий правильное соотношение частей 2. Например, размеры модели машины или сооружения отличаются от размеров оригинала одним и тем же множителем, задающим масштаб модели. Пропорции начали изучать в Древней Греции. Сначала рассматривали только пропорции, составляемые из натуральных чисел.
В IV веке до н. э. Дрвнегреческий математик Евдокс дал определение пропорции, составленной из величин любой природы. Древнегреческие математики с помощью пропорций решали задачи, которые в настоящее решают с помощью уравнений, выполняли алгебраические преобразования, переходя от одной пропорции к другой.
С помощью букв пропорция записывается так:
а: в = с: d или а/в = с/d, где а, в, с, к не равны нулю.
1. Решить уравнение: 6,4:0,16=4:х
1) 10; 2) 2,5; 3) 0,1; 4) 1.
2. Решить задачу:
Для 10 порций салата требуется 200г лука. На сколько порций хватит 60г лука?
1) 3; 2) 4; 3) 2; 4) 9.
8. Подведение итогов урока. Рефлексия.
Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).
Вам для этого помогут слова:
-Я узнал…
-Я почувствовал…
-Я увидел…
-Я сначала испугался, а потом…
-Я заметил, что …
-Я сейчас слушаю и думаю…
-Мне интересно следить за…
9. Домашнее задание.
Выучить п.14.
Решить № 491, 495, 485.
Говорят, что математика – гимнастика ума, я надеюсь, что сегодняшний урок, стал для вас хорошей тренировкой, которая позволила стать более внимательными, собранными, сообразительными, заставила думать и творить что-то новое.
Тема: Решение текстовых задач составлением систем уравнений с двумя переменными.
Цели урока:
закрепить умения учащихся решать текстовые задачи составлением систем уравнений второй степени с двумя переменными;
развивать логическое мышление, математическую речь, вычислительные навыки;
формирование умения работать в группе.
Ход урока.
1. Организационный момент.
Начинаем урок,
Он пойдёт ребятам впрок,
Постарайтесь всё понять,
Учитесь тайны открывать,
Ответы полные давать,
Чтоб за работу получать
Только лишь отметку 12.
2.Мотивация урока.
Девизом нашего урока является высказывание: “Есть в математике нечто, вызывающее человеческий восторг”, так как на уроках алгебры очень важно уметь, смотреть и видеть, замечать и отмечать различные особенности. Даю “установку”: Развивать и тренировать свое алгебраическое зрение.
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
3. Актуализация опорных знаний. Проверка д/з.
Вопросы для повторения:
1. Что называется системой уравнения с двумя переменными.
2. Что значит решить систему уравнений с двумя переменными.
3. В чем заключается графический способ решения систем уравнений с двумя переменными?
4. Какой порядок действий при решении систем уравнений способом подстановки?
5. Что называется графиком уравнения с двумя переменными?
6. Схема решения задач составлением системы уравнений с двумя переменными:
Анализ условия
Выделения двух ситуаций
Введение неизвестных
Установление зависимости между данными задачи и неизвестными
Составление уравнений
Решение системы уравнений
Запись ответа
4.Решение текстовых задач составлением систем уравнений с двумя переменными.
Решить № 448(5), 455, 498.
5. Динамическая пауза.
Раз! Два! Час вставати,
Будемо відпочивати
Три! Чотири! Посідаймо.
Швидко втому проганяймо.
П’ять! Шість! Засміялись,
Кілька раз понахилялись
Зайчик сонячний, до нас
Завітав у світлий клас
Будемо бігати, стрибати
Щоб нам, зайчика впіймати.
Прудко зайчик утікає
І промінчиками грає.
Сім, вісім! Час настав
Повернутися до справ.
6.Самостоятельная работа.
Задания для повторения (из курса «Алгебра 7 класс»)
Решение уравнений.
Что такое уравнение?
Что значит решить уравнение?
Алгоритм решения уравнения.
Решить № 106(1, 2)
Решить самостоятельно № 106(4).
7. Подведение итогов урока. Рефлексия. Д/з.
Сегодняшний урок мне позволил …
Я никогда не думал, что …
Невероятно интересным на уроке было …
Я усвоил тему
Я недостаточно усвоил тему, но могу дома разобраться самостоятельно
Я не усвоил тему, обращусь за помощью к учителю
Повторить п.13, 14. Решить № 456, 498, 448(4).
Тема: Обобщение и систематизация знаний по теме «Системы уравнений второй степени с двумя переменными»
Цели урока:
обобщить и систематизировать навыки и умения учащихся применять системы уравнений при решении задач; формирование умения переносить знания в новую ситуацию;
развивать логическое мышление, математическую речь, вычислительные навыки;
формирование умения работать в группе.
Ход урок:
1. Организационный момент
Ребята, послушайте, какая тишина!
Это в школе начались уроки.
Мы не будем тратить время зря,
И приступим все к работе.
Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:
- Что есть больше всего на свете? – Пространство.
- Что быстрее всего? – Ум.
- Что мудрее всего? – Время.
- Что приятнее всего? – Достичь желаемого.
Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.
2. Мотивация урока.
3. Актуализация опорных знаний. Проверка д/з.(сверка с доской №434)
Фронтальный опрос:
Вопросы:
Что называется системой уравнений?
Что называют решением системы?
Что значит решить систему уравнений?
Сформулируй алгоритм решения системы уравнений графически.
Сформулируй алгоритм решения системы методом подстановки.
Алгоритм решения задач составлением системы уравнений с двумя переменными
Математический диктант.
Два ученика выполняют диктант у доски по вариантам на скрытой доске.
1 вариант.
Составьте уравнение с двумя переменными, если:
Сумма двух натуральных чисел равна 16.
Периметр прямоугольника равен 12 см.
Одна сторона прямоугольника на 8 см больше другой.
Произведение двух натуральных чисел равно 28.
Диагональ прямоугольника равна 5 см.
2 вариант
Составьте уравнение с двумя переменными, если:
Разность двух натуральных чисел равна 14.
Площадь прямоугольника равна 26 см?.
Катет прямоугольного треугольника на 5 см больше другого.
Сумма квадратов двух натуральных чисел равна 30.
Гипотенуза прямоугольного треугольника равна 8 см.
4. Обобщение и систематизация знаний по теме «Системы уравнений второй степени с двумя переменными»
1этап: Найти решение системы уравнений с двумя переменными.
у-х=2,
ху-у=10
А) (3; 5); Б) (5; 3); В) (1;-3); Г)(-3; 2).
2 этап: Какие фигуры являются графиками системы уравнений?
+
=5,
ху=-3.
А) прямая и парабола;
Б) окружность и парабола;
В) окружность и гипербола;
Г) парабола и гипербола.
3 этап: Решить систему графическим способом № 933(4).
4 этап: Решить систему способом подстановки № 934(1).
5 этап: Решить задачу составлением системы уравнений с двумя переменными № 938.
Придумайте задачу о прямоугольнике, решение которой приводит к системе:
6. Физкультминутка.
Дружно с вами мы считали, о системах рассуждали,
А теперь мы дружно встали, свои косточки размяли.
На счет раз кулак сожмем, на счет два в локтях сожмем.
На счет три — прижмем к плечам, на 4 — к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем — добрыми всегда мы будем.
На счет шесть прошу всех сесть.
Числа, я, и вы, друзья, вместе дружная 7-я.
7. Самостоятельная работа.
Самостоятельная работа на 3 варианта на все типы систем. Работать будете в парах. После решения самостоятельно проверяем по готовым ответам.
1 вариант:
2 вариант:
3 вариант:
Ответы записаны на ватмане. 1 вариант: (3;3), (-1;1)
2 вариант: (7;-1), (-1;7)
3 вариант: (5;2)
8. Подведение итогов урока.
Рефлексия:
что понравилось (не понравилось)
что вызвало трудности (легко)
что повторили
вы получили высокие оценки или нет
(Выслушиваются ответы).
Давайте подведем итог нашей работы.
Задача может быть решена несколькими способами. Решение зависит и от самой задачи, и от человека, который ее решает, от тех методов, которыми он владеет, от уровня его знаний и его умений.
Но очень хорошо, если ученик, решив задачу, пытается найти другой способ решения. Ведь и в жизни нам очень часто приходится искать решение какой-то проблемы. Иногда решений несколько, а иногда мы с большим трудом находим одно - единственное.
9. Домашнее задание.
Повторить п.13, 14.
Решить № 939, 933(2), 934(3).
Попробуйте к следующему уроку сами составить задачу, которая решается с помощью системы линейных уравнений.
Спасибо за урок!
Тема: Контрольная работа по теме «Системы уравнений с двумя переменными».
Цели:
1. Проверить знания, умения и навыки учащихся по теме «Системы уравнений с двумя переменными».
2. Развивать внимание, логическое мышление, письменную математическую речь;
3. Воспитывать самостоятельность, трудолюбие.
Ход урока
1.Организационный момент.
2.Мотивация урока.
3. Контрольная работа
4. Итоги урока.
Повторить п. 13, 14.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок по теме "Решение систем уравнений второй степени с двумя переменными"9 класс (273.39 KB)
Урок по теме "Решение систем уравнений второй степени с двумя переменными"9 класс (273.39 KB)
 0
0 2208
2208 238
238 Нравится
0
Нравится
0


