Тема урока:
Кейс «Применение производной при решении задач ЕГЭ».
«Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы: движение».
Ф.ЭНГЕЛЬС.
(КЕЙС, а, м. [англ. case дипломат)
ТЕМА ЗАНЯТИЯ: Кейс «Применение производной при решении задач ЕГЭ».
ЦЕЛИ УРОКА:
Учебные:
Повторить теоретические сведения по теме, необходимые для решения рассматриваемых задач.
Обобщить, закрепить и углубить имеющиеся знания по теме «Производная».
Научить применять полученные теоретические знания при решении различного типа математических задач.
Подготовка к ЕГЭ. Разработка рекомендаций к системе подготовки по решению задач типа заданий №№11 профильного теста.
Воспитательные:
Обучение навыкам: планирования деятельности, работы в оптимальном темпе, работы в группах, подведения итогов.
Развитие умения оценивать свои способности, свое положение в паре, умение контактировать с товарищами.
Воспитывать чувства ответственности и сопереживания.
Способствовать воспитанию умения работать в команде; умения критически относиться к мнению одноклассников.
Развивающие:
Развивать у учащихся умение находить нужную справочную литературу, самостоятельно добывать знания, учить самодиагностике.
Учить формированию ключевых понятий изучаемой темы.
Развитие исследовательских навыков. Развитие умения анализировать, систематизировать, интерпретировать полученные результаты.
Тип урока: комбинированный: обобщение, закрепление навыков применения свойств элементарных функций, применение уже сформированных знаний, умений и навыков применения производной в нестандартных ситуациях.
Оборудование: ноутбук, проектор, экран, раздаточный материал.
Основные этапы урока.
Организационная деятельность. Слово учителя.
Актуализация знаний учащихся.
Устный счёт.
Работа с кейсом. Анализ.
Домашнее задание.
Итог урока.
ХОД УРОКА.
Вступительное слово учителя.
Анализируя результаты итоговой аттестации за 3 последние года, можно сделать вывод о том, что с заданиями математического анализа, а это задания на применение производной , ее физического , геометрического смысла из работы ЕГЭ, справляются не более 30-35% выпускников. Вот и в нашем классе по результатам тренировочных и диагностических работ верно выполняют их в среднем 5-6 человек. Этим и обусловлен наш выбор, отрабатываем навык применения производной при решении задач ЕГЭ.
Сегодня на уроке мы продолжаем работать с «кейсом». (КЕЙС - лат. capsa ящик, футляр. То же, что дипломат) Под учебным кейсом понимается несколько страниц текста, различные презентации, видеоматериал. Сейчас у каждого из вас на столе кейс. В течение двух занятий вы работали с данным с ним.
1 урок. Сообщение темы работы.
Индивидуальное изучение кейса каждым учеником. Подбор заданий по теме.
Разработка вариантов индивидуальных решений.
2 урок. Обсуждение вариантов индивидуальных решений в каждой группе.
Вопросы для обсуждения. Подготовка презентаций.
В начале первого занятия учащиеся класса были разбиты на 3 группы. Каждой группе в бумажном виде были предложены: текст мини - кейса, образцы задач, вызывавших затруднения, подсказки, вспомогательные вопросы, задания.
II. Представление кейса.
1. Чтение вслух текста из кейса "Производная и ЕГЭ"
Сравните задания, данные каждой группе и сформулируйте цели работы.
3. Итак, цель полезного использования нашего кейса: повторить способы решения подобных задач и убедиться в преимуществах выбранной методики.
4. Кроме того, если вы были внимательны при изучении кейса, вы должны обратить внимание на ещё одно задание, сформулированное в нём в косвенной форме. (???) Найдите в тексте.
«Помимо проблемы итоговой аттестации возникают вопросы и сомнения, в какой мере приобретаемые в этой области знания могут и будут востребованы в дальнейшем, насколько оправданы как затраты времени, так и здоровья на изучение этой темы».
Зачем нужна производная? Где мы встречаемся с производной и используем её? Можно ли без нее обойтись в математике и не только?
1 группа. Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д., так как механический смысл производной - это мгновенная скорость.
Производную применяют для исследования функции и построения ее графика, для нахождения наибольшего и наименьшего значений функции.
Слова «производная» и «произошло» имеют похожие части слова, да и смысл похож: производная происходит от исходной функции (переложив на отношения человека: исходная функция - «мама», её производная «дочь»). Производная - часть математической науки, одно из её звеньев. Нет этого звена - прерваны связи между многими понятиями.
2 группа. Актуальность темы “Производная в школьном курсе математики” следует из того, что человек в повседневной деятельности постоянно сталкивается с решением задач, которые могут быть полностью описаны с помощью функций на математическом языке, а между тем производная является мощным орудием исследования функций. Тема “Производная и ее применения” является одним из основных разделов начал математического анализа. При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница, который использовал понятие бесконечно малой. Ньютон пришёл к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени (мгновенной скорости).
3 группа. Оказывается также, что с помощью производной можно упрощать алгебраические и тригонометрические выражения, раскладывать на множители, доказывать тождества и неравенства и, даже, решать вопрос о существовании корней квадратного уравнения.
На практике часто приходится решать так называемые задачи на оптимизацию (optimum-наилучший) . Инженеры-технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции; конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей; экономисты стараются спланировать связи завода с источниками сырья так , чтобы транспортные расходы оказались минимальными и т.д.
Можно сделать вывод, что производная – одно из самых важных понятий математического анализа. Знание производной позволяет решать многочисленные задачи по экономической теории, физике, алгебре и геометрии.
5. Актуализация знаний учащихся.
Для выполнения заданий кейса какие знания и умения вам пригодились?
-формулы и правила дифференцирования.
Повторим их. Взаимопроверка правил и формул по карточкам контроля.
Устный счёт.
Найти производные функций:
1) f(x) = cos 3x
А) 3cos x ; Б) -3sin 3 x ; В) cos 3x ; Г) 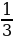 sin 3 x.
sin 3 x.
2) f(x) = 4x3 –x2
А) 4x3-2x ; Б) 12x 3-2x ; В) 12x 2 -2x ; Г)12x2 –x;
3) f(x) = e2x
А) e2x ; Б) 2 e2x ; В) 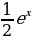 ; Г) 2
; Г) 2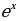 .
.
4) f(x) = 2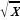
А)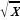 ; Б)
; Б) 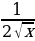 ; В)
; В)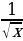 ; Г)
; Г)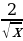 .
.
5) f(x) = ln (5-x)
А) ln x ; Б) - ln (5-x) ; В) 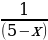 ; Г) -
; Г) - 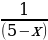 .
.
6) f(x) =  sin 3 x
sin 3 x
А) 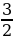 cos 3x; Б)
cos 3x; Б)  cos 3x ; В)
cos 3x ; В)  cos x; Г) -
cos x; Г) -  cos 3x.
cos 3x.
7) f(x) = 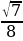 π x
π x
А)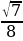 π; Б) х; В)
π; Б) х; В)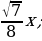 Г) π.
Г) π.
7.Работа с кейсом. Защита своих идей. Представление презентаций каждой группой.
Представляют пример своего случая, объясняют решение одной задачи, соответствующей заданию кейса.
1 группа - Применение производной для нахождения наибольшего и наименьшего значений функции на указанном промежутке.
2 группа - Применение производной для нахождения наибольшего и наименьшего значений функции без указания числового промежутка.
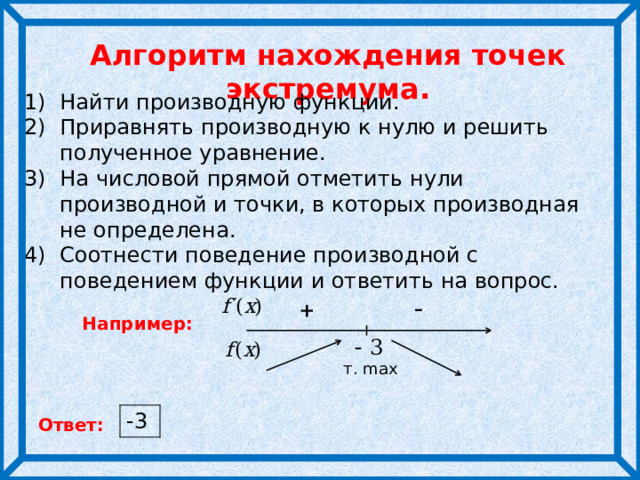
3 группа - Применение производной для нахождения точек экстремума функции.
ЗАДАНИЯ ГРУППАМ. От каждой группы разработать и предоставить на уроке рекомендации к системе подготовки решения заданий на применение производной. Доказать преимущества вашей методики.
8. Физ.пауза. 1.Наклон головы вперёд-назад.
2.Наклон головы влево-вправо.
3.Описать головой полукруг.
4.Руки вперёд, кисти «замком», повороты сцепленными руками влево-вправо.
5.Руки вниз, поднимаем и опускаем плечи.
9. Работа в группах.
После каждого представления решают в группах ещё одно задание.
10. ПРОЕКТ ПРЕДЛОЖЕНИЙ, как общий вывод, записывается в тетрадь.
ЗАДАНИЯ ГРУППАМ. От каждой группы разработать и предоставить на уроке рекомендации к системе подготовки решения заданий типа В11. Доказать преимущества вашей методики.
11. Попробуйте объяснить, для чего лично вам может пригодиться сегодняшнее занятие?
12. Рефлексия. Заполнение оценочного листа.
13. Домашнее задание. Подготовка к контрольно-зачетной работе.
Закончить работу с прототипами заданий на производную и ее применение, используя полученные на уроке ВЫВОДЫ.
Найдите наибольшее значение функции y=4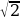
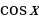 +4x –π на отрезке [0 ;
+4x –π на отрезке [0 ;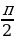 ] .
] .
Найдите наименьшее значение функции 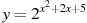 .
.
Найдите точку минимума функции 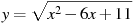 .
.
Найдите наименьшее значение функции 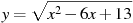 .
.
Найдите точку минимума функции 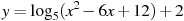 .
.
Найдите наибольшее значение функции 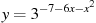 .
.
Найти наименьшее значение функции y =3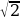 sinx +3
sinx +3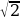 x на отрезке [0;
x на отрезке [0; 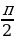 ]
]
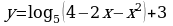 3.Найдите наибольшее значение функции
3.Найдите наибольшее значение функции 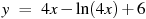 на отрезке
на отрезке 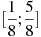 .
. 
 Получите свидетельство
Получите свидетельство Вход
Вход


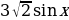 +
+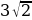 х на отрезке [0;
х на отрезке [0; 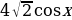 +
+ 4х-
4х-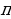 на отрезке [0;
на отрезке [0; 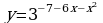 . Найти наименьшее значение функции у =(х+7)ех+8 на отрезке [-9; -7]
. Найти наименьшее значение функции у =(х+7)ех+8 на отрезке [-9; -7]  . Найдите наибольшее значение функции
. Найдите наибольшее значение функции 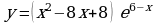
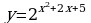 . Найдите наименьшее значение функции
. Найдите наименьшее значение функции 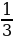
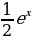
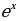
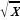
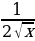
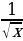
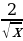
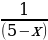

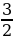
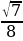
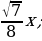
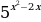
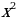 -5
-5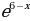
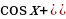 6
6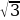
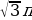 +6 на отрезке [
+6 на отрезке [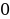 ;
; 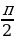 ]
]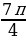 -7
-7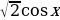 на отрезке [
на отрезке [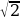
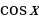 +4
+4










 0 . Функция y= возрастающая. Рассмотрим функцию f(x)=4-2x-, графиком является парабола с ветвями, направленными вниз, следовательно, наибольшее значение f(x) в вершине параболы ,т.е. при х= = =-1. f(-1)=4+2-1=5 Значит, =1+3=4. 5 Ответ:4." width="640"
0 . Функция y= возрастающая. Рассмотрим функцию f(x)=4-2x-, графиком является парабола с ветвями, направленными вниз, следовательно, наибольшее значение f(x) в вершине параболы ,т.е. при х= = =-1. f(-1)=4+2-1=5 Значит, =1+3=4. 5 Ответ:4." width="640"




![Найдите наибольшее значение функции y =2 x +4 на отрезке [; 0] Найдём производную функции y =2 x +4. y′= -2 - . Найдём критические точки : -2 - = 0 , -2 = , = - - уравнение корней не имеет, значит, критических точек нет. y() = 2 * +4 =2*(-) +8+4= -1+12=11 y(0)= 2-0+4=6. Ответ: =11.](https://fsd.videouroki.net/html/2023/11/16/v_6555ce4bbf0ea/img_v99795936_4_18.jpg)



![Решите в группах : Найдите наибольшее значение функции y =6 + 2 на отрезке [0;] ОТВЕТ: -2.](https://fsd.videouroki.net/html/2023/11/16/v_6555ce4bbf0ea/img_v99795936_4_23.jpg)














 Урок по теме Производная (2.23 MB)
Урок по теме Производная (2.23 MB)
 0
0 350
350 3
3 Нравится
0
Нравится
0






