Урок математики
по теме:
«Уравнение и его корни»
5 класс
Учебник: под ред. Виленкина Н.Я.
Тип урока: комбинированный урок.
Цели урока:
а) образовательные:. сформировать представление об уравнении как предложении с переменной, ввести в речевую практику понятие корня уравнения; отработать алгоритм нахождения неизвестных компонентов уравнения; вместе с учащимися учиться выбирать способы решения уравнений в зависимости от условий;
б) развивающие: развивать математическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания;
в) воспитательные: развивать личностные качества учащихся, таких как целеустремленность, настойчивость, аккуратность, умение работать в коллективе.
Методы обучения: наглядный, словесный, практический, частично-поисковый, репродуктивный.
Формы работы учащихся: фронтальная работа.
Необходимое техническое оборудование: доска, компьютер, мультимедийный проектор, экран
Основные понятия: уравнение, корень уравнения, решить уравнение.
Межпредметное понятие: корень
Предметное понятие: корень уравнения
Планируемый результат:
Личностные: самопознание,
самооценивание,
формирование целостного мировоззрения,
смыслообразование
Метапредметные: формирование
Регулятивных УУД: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
Коммуникативных УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Познавательных УУД: умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Предметные: Понимание, что такое «уравнение», «корень уравнения», «решение уравнений»
Умение решать уравнения вида а + х = b, а – х = b, х – а = b. на основе зависимостей между компонентами арифметических действий;
Ход урока.
| Этапы урока | Деятельность учителя | Деятельность учащихся | ||||||||||||||||||
| I. Подготовитель- ный этап | Учитель читает пожелания: Прозвенел звонок весёлый. Вы начать урок готовы? Будем слушать, рассуждать, И друг другу помогать! Улыбнёмся друг другу, пожелаем удачи. (хлопки в ладони друг другу) - Что вам пригодится для успешной работы? - Какое нужно настроение, чтобы урок для вас был удачным? - Я желаю вам сохранить хорошее настроение весь урок. Я верю в вас, у вас всё получится. - Ребята, а вы любите тайны и секреты? - Сегодня на уроке нам предстоит научиться раскрывать что-то тайное и неизвестное. Вы готовы? Вам интересно? - Что ж отправляемся в царство математики совершать новые открытия. Название нашего урока «Основа, на которой все держится». (на слайде) Как вы думаете, о чем это? Но у каждого урока должна быть тема…... | Включаются в учебную деятельность.
Учитель и дети приветствуют друг друга смайликами-настроения.
Отвечают на вопросы учителя. | ||||||||||||||||||
| Устный счет | Ребята, на доске зашифровано слово, которое имеет прямое отношение к теме нашего урока, разгадайте его. На листочке записывайте только ответы. 1)120-20*4 А 2)215-(115+97) У 3)(549+298)-249 Е 4)15+420:4 Н 5)(296+157)-146 Р 6)11+23+27+39+29 И 7)56-27+44 В
Но это только половина нашей темы урока. Давайте же вместе узнаем вторую половину названия темы урока. | Решают примеры с использованием изученных свойств сложения и вычитания | ||||||||||||||||||
| Формирование обобщенного представления о межпредметном понятии Выявление субъектного опыта Актуализация знаний | Что изображено на рисунках? 3 + Х = 5 Х - ? Загадка: Я у дуба, Я у зуба, Я у слов И у цветов. Я упрятан в темноту. Я не вверх, а вниз расту √а
Что такое корень? Запишите на рабочих листах Давайте обратимся к толковому словарю, узнаем значение этого слова.(слайд) 1) Подземная часть растения, служащая, для укрепления его в почве и всасывания из нее воды и питательных веществ. Например: пустить корни. Ребята, как вы думаете кто и когда даст нам ответ на этот вопрос? Обясните следующие фразы: Корень зла В корне неправильно Коренная перестройка Смотри в корень или зри в корень Значит, корень – это основа чего – то. Слово «корень» имеет несколько значений, оно является многозначным. Можно ли употреблять слово одно слово корень? (нет) Обязательно корень чего - то О каких корнях пойдет сегодня речь на нашем уроке? О корне уравнения. Сегодня мы с вами будем работать с уравнениями, с корнями уравнений. Сформулируйте тему нашего урока и его цель. А что такое уравнение? Среди записей найдите уравнения(слайд) 25 13 15 + 8 = 23 a + b =b+ a 18 + Х = 56 138 – Х У – 7 = 20 (Х+ 10) – 3 = 17 Сформулируйте, что такое уравнение? (равенство, содержащее букву, значение которой надо найти) Уравнение – это: Равенство Содержит букву Что значит решить уравнение? (найти значение буквы) А что такое корень уравнения? Запишите на рабочих листах | Отвечают на поставленные вопросы. Осмысление собственного опыта. Проговаривают то, что знают. Выполняют задание устно, письменно Предлагают разные варианты. Осмысление собственного опыта, Познание нового Учащиеся зачитывают все значения слова корень). Слушают наводящие вопросы учителя и вместе формулируют цели урока, определения уравнения, корня уравнения, алгоритм нахождения неизвестного компонента | ||||||||||||||||||
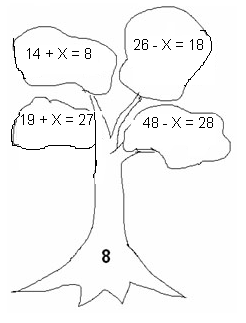
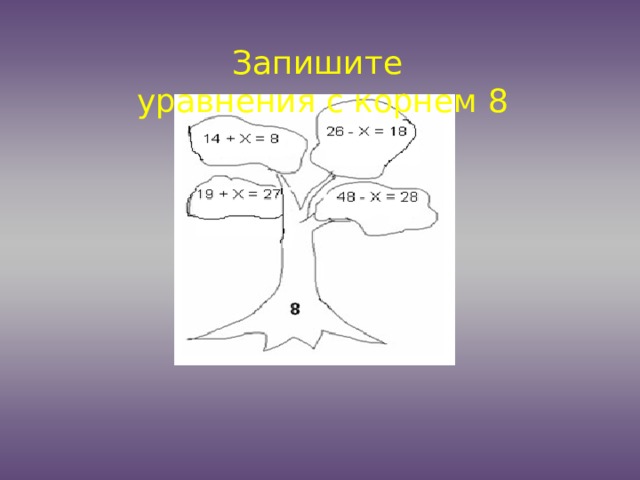
| II Основной этап. Формулировка определения и запись в алгоритмизированном виде Работа с определением Первичное закрепление | Что вы видите на дереве? (уравнения) Запишите уравнения с корнем 8. Почему вы выбрали именно эти? (при подстановке вместо буквы получалось верное числовое равенство) Что –же такое корень уравнения? (значение буквы, при котором уравнение превращается в верное числовое равенство) Вывод: Корень уравнения- это число (значение буквы) при подстановке в уравнение получается верное числовое равенство Давайте прочитаем определения корня уравнения в учебнике, откройте стр. 59. Вспомним героев мультфильма «Незнайка и его друзья» Незнайку и Знайку. Как вы думаете, кому принадлежит следующее высказывание: Корень уравнения – это буква (Н) Корень уравнения – это фигура (Н) Корень уравнения – это значение буквы (Н) Корень уравнения – это значение буквы, которое надо подставить в уравнение (Н) Корень уравнения – это число (Н) Корень уравнения – это значение буквы, при котором уравнение превращается в верное числовое равенство (З) Корень уравнения – это число, при котором уравнение превращается в верное числовое равенство (З) Корень уравнения - основа зуба (Н) Что значит решить уравнение? (найти его корни) Какие из чисел 0, 1, 2, 3 являются корнем уравнения Х + 3 = 6 Умеете ли вы решать уравнения? Решите уравнения Х + 14 = 36 Х – 23 = 95 95 – Х = 23 Взаимопроверка. Работа в парах. Назовите корни уравнения А как вы решили 1 уравнение? Действием вычитанием. Находим неизвестное слагаемое Как решили 2 уравнение? Действием сложением. Находим неизвестное уменьшаемое Как решили 3 уравнение? Действием вычитанием. Находим неизвестное вычитаемое Молодцы! | Взаимопроверка. Работа в парах. Учащиеся зачитывают свои уравнения Выполняют задание . Предлагают свои варианты. Отвечают смайликами (радостный-Знайка,грустный-Незнайка) По учебнику читают Сравнивают свой вывод с выводом в учебнике Решают уравнения на доске 3 ученика, остальные самостоятель-но | ||||||||||||||||||
| Физкультминутка. | (проводит один из учеников) Быстро встали, улыбнулись. Выше-выше потянулись. Ну-ка плечи распрямите, Поднимите, опустите. Вправо, влево повернитесь, Рук коленями коснитесь. Сели, встали. Сели, встали. И на месте побежали. Поднимает руки класс-это «раз»(хором все) Повернулась голова -это «два» Руки вниз, вперед смотри- это «три» Руки в стороны пошире развернули на «четыре» С силой их к плечам прижать- это «пять» Всем ребятам надо сесть –это «шесть» | Выполняют упражнения | ||||||||||||||||||
| Проблемная ситуация, связанная с возможным количеством корней уравнений | Работа в парах А как вы думаете, ребята, уравнения могут иметь только один корень? 2) Решите уравнение и сделайте вывод.
Уравнение b + 40= 60 имеет один корень. На рабочих листах заполните таблицу и сделайте вывод. Вывод: Уравнение может иметь один корень Запишите и найдите корень уравнения: а : а = 1 Сколько корней может иметь это уравнение? Много. Вместо а можно поставить любые числа. Какое только число нельзя подставить в это равенство (на что нельзя делить)? = Нельзя делить на 0. Какой вывод можно сделать? = Вывод: уравнение может иметь несколько корней. 2) Решите уравнение и сделайте вывод.
Уравнение 0 ∙ х = 7 не имеет корней. На рабочих листах заполните таблицу и сделайте вывод. Вывод: Уравнение может иметь разное количество корней | Работают в парах с последующей взаимопроверкой | ||||||||||||||||||
| Самостоятельная работа с самопровер кой по эталону. | Посмотрим на уравнения в № 372. Сколько корней имеет каждое из них? (1) Назовите уравнения, которые решаются вычитанием. Самопроверка по эталону (на доске) - У кого всё правильно? - У кого есть ошибки? - Где ошибка? - В чём причина? Самооценка. Посмотрите на уравнения, записанные на доске. Чем похожи уравнения каждого столбика? I группа – простые уравнения. На следующем уроке научимся решать сложные уравнения. | Выполняют задание в тетради. Выполняют самопроверку по ответам на закрытой части доски | ||||||||||||||||||
| Домашнее задание | Запишите в дневники домашнее задание П. 10, № 395 (а, в, д) – решить 3 уравнения № 403 (а) – решить пример в несколько действий | | ||||||||||||||||||
| Рефлексия учебной деятельности Выявление субъектного опыта | Подведем итог нашего урока Какая была цель урока? Что узнали на уроке? Что общего у всех значений слова корень? Что такое корень уравнения? (исправьте другим цветом ваши определения в рабочих листах) Досочиняйте стихотворениена рабочих листах ( вместо точек выберите и напишите слова, подходящие по смыслу, записанные на доске) Когда уравненье решаешь, дружок, Ты должен найти у него …….. Значение буквы проверить несложно, Поставь в …………………. его осторожно. Коль верное ……………выйдет у вас, То …………….. значенье зовите тотчас. Какие слова надо вставить вместо точек ? Прочитаем хором получившееся стихотворение Когда уравненье решаешь, дружок, Ты должен найти у него корешок Значение буквы проверить несложно, Поставь в уравненье его осторожно. Коль верное равенство выйдет у вас, То корнем значенье зовите тотчас. Ребята,хотите ли ещё встретиться с «Мистером Х» - корнем уравнения? Учитель прощается с учениками- показывает смайлик-настроение от урока | Отвечают на вопросы учителя. рассказывают, что узнали, знают, смогли. Делают самооценку .Выставляем оценки ,ученикам, работавшим у доски. Сдают рабочие листки. Дети показывают смайлики-с каким настроением они уходят с урока |
Рабочий лист к уроку по теме «Уравнение и его корни»
|
| Самооценка/взаимооценка | ||||||
| Корень –
|
| ||||||
| Корень уравнения –
|
| ||||||
| Решите уравнения: Х + 14 = 36 Х-23=95 95-Х=23
|
| ||||||
| Заполните таблицу: Сколько корней имеет каждое уравнение?
| | ||||||
| Вставь пропущенные слова Когда уравненье решаешь, дружок, Ты должен найти у него …….. Значение буквы проверить несложно, Поставь в …………………. его осторожно. Коль верное …………… выйдет у вас, То …………….. значенье зовите тотчас. | |
4

 Получите свидетельство
Получите свидетельство Вход
Вход


























 13 2) 15 + 8 = 23 3) a + b = b + a 4) 18 + x = 56 5) 138 – x 6) y – 7 = 20 7) (x + 10) – 3 = 17" width="640"
13 2) 15 + 8 = 23 3) a + b = b + a 4) 18 + x = 56 5) 138 – x 6) y – 7 = 20 7) (x + 10) – 3 = 17" width="640"






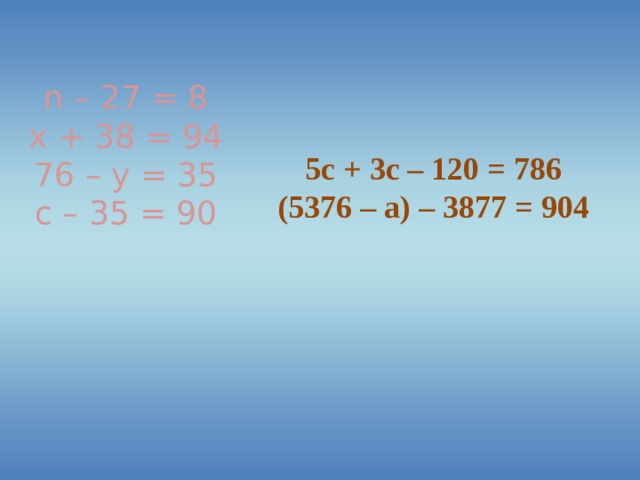











 Урок математики по теме: «Уравнение и его корни» 5 класс (1.14 MB)
Урок математики по теме: «Уравнение и его корни» 5 класс (1.14 MB)
 0
0 245
245 14
14 Нравится
0
Нравится
0


