ЦЕЛИ УРОКА:
1. Продолжить работать над алгебраическим способом решения задач на смешивание растворов и применять математический аппарат при решении задач химического содержания.
2. Развивать у обучающихся желания и потребности обобщения изучаемых факторов.
3. Способствовать развитию творческого мышления, самостоятельности и творчества при изучении данной темы.
ХОД УРОКА
1. Орг момент.
Учитель. Сегодня на уроке мы продолжим работать над задачами на смешивание растворов алгебраическим методом и рассмотрим новый способ решения этих задач под названием «Конверт Пирсона», который позволяет рационально распределить время при решении задач на растворы.
В последнее время в учебниках по математике, начиная с 5 - го класса появилось много задач химического содержания на растворы, поэтому поняв химическую сущность задачи и применив математический аппарат, можно быстро справиться с задачей, тем более, что вы владеете некоторой химической терминологией, благодаря предмету «Введение в химию», который вы начали изучать в этом году.
2. Актуализация знаний.
Вспомним основные моменты, которые нам понадобятся на уроке.
Работаем устно:
1. В чём заключается основное свойство пропорции?
2. Как найти неизвестный средний член пропорции?
3. Как найти неизвестный крайний член пропорции?
4. Из каких компонентов состоит раствор?
5. Из чего складывается масса раствора?
6. Что называется массовой долей растворённого вещества?
7. В чём измеряется массовая доля растворённого вещества?
8. Когда массовая доля растворённого вещества измеряется в процентах?
9. Что показывает массовая доля растворённого вещества?
10. 25% раствор. Что это значит?
11. Сколько г соли содержится в 450г 10% - го раствора?
12. 5г соли растворили в 10г жидкости. Определить процентную концентрацию раствора.
3. Изучение нового материала.
Учитель: А теперь представим себе, что мы учимся в 11 - м классе и очень скоро нам сдавать ЕГЭ. Оказывается, эту задачу можно решить с помощью нового метода под названием «Конверт Пирсона» или метод «креста»:
При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
Смотрите документ
При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения (метод креста) или квадрат Пирсона. Разберем этот метод на примере решения задачи.
Задача. Один раствор содержит 20% соли. А второй — 70%. Сколько граммов первого и второго растворов нужно взять. Чтобы получить 100 г 50% - го солевого раствора?
Решение: Решим задачу по правилу «креста». Составим схему.(смотрите документ)
Значит, 10 г смеси составляют 50 частей. Одна часть — 100 :(30 + 20) = 2 г,
70 - ый раствор - 2· 30 = 60 г. , а 20% раствор – 2 · 20 = 40 г.
Ответ: 20% - 40 г, 70% — 60 г.
Теперь решите самостоятельно.
Задача. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1, 5%?
Старинный способ решения задач на смешивание двух веществ (метод рыбки)
Задача.
У некоторого человека были на продажу масла двух сортов: одно ценою 10 гривен за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла ценою 7 гривен?
Из схемы делаем заключение, что дешевого масла нужно взять втрое больше, чем дорогого, т. е. для получения одного ведра ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого масла 3/4.
Конверт Пирсона в квадрате!
Сегодня мы рассмотрим еще один оригинальный способ решения задач на концентрацию и решим одну из них разными способами. Итак…
Условие задачи: Даны 70% и 10% растворы. Сколько нужно взять каждого из этих растворов, чтобы получилось 600 грамм 30% раствора.
Сначала решим задачу способом, который известен всем нам, то есть алгебраическим. За величину Х возьмем количество взятого 70% раствора, следовательно, 600 - Х – количество взятого 10% раствора. Как мы знаем, 70%=0, 7, 10%=0, 1, а 30%=0, 3. Составим уравнение, находим Х. Х = 200 грамм, это количество 70% раствора, следовательно, 600 - Х=600 - 200=400 граммов 10% раствора.
Сейчас мы познакомим вас с более удобным и оригинальным способом решения этой задачи, который носит название «конверт Пирсона» квадрате. Этот способ предложил английский математик и статистик Карл Пирсон.
Мы имеем 70% раствор, 10% раствор. Нужно получить 600 грамм 30% раствора.
|
70% |
600гр |
20 |
|
600гр |
30% |
60 |
|
10% |
30% |
40 |
Из 30 вычитаем 10, в правый верхний угол записываем 20. Из 70 вычитаем 30, в правый нижний угол записываем 40. Складываем получившиеся результаты и записываем во вторую строку справа. 40+20=60. Количество раствора делим на последний результат, т. е. 600/60=10. 10 умножаем на 20 и 40, получаем ответ, 400 и 200 грамм.
Немного истории и любопытных фактов. (Сообщение готовит обучающийся как дополнительное дом. зад. )
А теперь немного о Пирсоне…Карл Пирсон родился 27 марта в 1857 году в Лондоне. Он был разносторонним человеком, активно изучал историю, математику, статистику и германистику. Большую часть 80 - х годов XIX века он провел в Берлине, Гейдельберге, Вене и Брикслеге. Интересовали его религия и поэзия – с одинаковым интересом он изучал Гёте и Священное Писание. Занимали Пирсона и вопросы пола – он даже основал Клуб Мужчин и Женщин. В 1898 году получил медаль Дарвина. Карл Пирсон Погиб в Англии в городе Суррее 27 апреля 1936 года. Прожил он 79 лет.
Как и все методы решений, конверт Пирсона имеет свои преимущества и недостатки. Одним из преимуществ этого способа является то, что он доступен ученикам, которые не умеют решать уравнения. Также квадрат Пирсона очень полезен для домохозяек, чтобы получать нужную концентрацию уксуса или сиропа.
Недостатком этого метода является то, что его можно применять только при смешивании двух растворов. То есть если нужно смешать три или более веществ, конверт Пирсона здесь не поможет.
Учитель. Итак, сделаем вывод: Для решения задач на проценты существует оригинальный метод решения «Конверт Пирсона». Он удобен для домохозяек, доступен ученикам, которые не умеют решать уравнения, но этот способ нельзя применять при смешивании трех и более растворов.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход


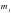 , а второго – через
, а второго – через 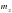 , то при смешивании общая масса смеси будет складываться из суммы этих масс.
, то при смешивании общая масса смеси будет складываться из суммы этих масс.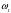 , во втором –
, во втором – 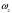 , а в их смеси –
, а в их смеси – 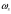 . Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах:
. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах: 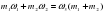 ,
, 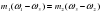
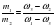

 ω1 ω3 — ω2
ω1 ω3 — ω2 
 ω3
ω3 
 20 20
20 20
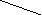 70 30
70 30 5% 1,5% 30 кг
5% 1,5% 30 кг

 1,5%
1,5%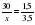
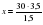
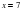
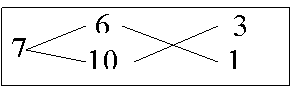









 Урок математики "Смеси, сплавы, концентрация" (60.62 КB)
Урок математики "Смеси, сплавы, концентрация" (60.62 КB)
 0
0 3005
3005 729
729 Нравится
0
Нравится
0


