Урок в 11 классе.
Шеина Е. Н.- учитель математики,
высшая квалификационная категория
Тема: Применение свойств функции при решении уравнений.
Форма проведения — комбинированный урок с элементами исследования.
Цель урока:
обобщение и закрепление знаний по теме « Функции и их графики»;
воспитание познавательного интереса к учебному предмету;
формирование умений анализировать, проводить обобщение, переносить знания в новую ситуацию.
Оборудование: плакаты с изображением графиков функций, карточки с заданием, Е.П. Нелин Учебник алгебра и начала анализа 10 кл, Г.П. Бевз, В.Г. Бевз Учебник алгебра и начала анализа 11 кл.
Ход урока:
1.Организационный момент.
Учитель: мы с вами закончили изучение всего программного материала. В рамках повторения на уроке рассматриваем вопрос о применение свойств функции при решении уравнений. Обращение к данной теме актуально, т.к. довольно часто встречаются уравнения, которые надо решать не традиционными способами. Кроме того решение таких уравнений с помощью свойств функций интересны, а некоторые из них необыкновенно красивы, а также позволяют экономить время. Я думаю, что в этом вы убедитесь сами. Работать будем по группам. Руководителями групп будут… (руководители в течение минуты распределяют обязанности в группе).
(2 мин)
2. Формулирование целей и задач урока.
В тетрадях записываем число, тему урока.
3. Проверка домашнего задания.
Дома вы повторяли свойства показательной, логарифмической, показательной и тригонометрических функций.
От каждой группы выступают теоретики с использованием плакатов, на которых изображены графики этих функций. В это же время на доске записывается решение уравнения из домашней работы 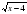 =6-x, способом возведения обеих частей в квадрат. (7 мин) 4. Актуализация опорных знаний.
=6-x, способом возведения обеих частей в квадрат. (7 мин) 4. Актуализация опорных знаний.
На доске записаны функции: 1) 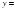
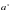 ; 2)
; 2) 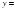
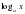 ; 3)
; 3) 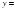
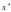 ; 4)
; 4) 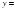
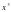 ; 5)
; 5) 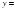
 ; 6)
; 6)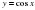 ; 7)
; 7) 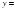
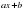 .
.
Назовите функции монотонные на всей области определения. Назовите функции, которые имеют наибольшее и наименьшее значение.
(3 мин)
5. Изучение нового материала.
Обратимся к решению уравнения из домашней работы. Его можно решить стандартным способом возведением обеих частей в квадрат как вы и сделали дома.
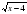 =
=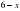
Решение: 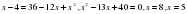 . Проверкой убеждаемся, что х=8 - посторонний корень. Ответ: 5
. Проверкой убеждаемся, что х=8 - посторонний корень. Ответ: 5
Можно рассуждать иначе. Левая часть уравнения является функцией возрастающей на всей области определения, а правая - убывающей на множестве R, а значит и при х 4. По теореме о корне, если в уравнении f(x)=g(x) функция f(x) возрастает на некотором промежутке, а функция g(x) убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более одного корня на этом промежутке. Если в уравнении f(x) = а функция f(x) возрастает или убывает на некотором промежутке, то это уравнение может иметь не более одного корня на этом промежутке. Решить уравнение - это значит найти все его корни или показать, что корней нет. Таким образом, уравнение
4. По теореме о корне, если в уравнении f(x)=g(x) функция f(x) возрастает на некотором промежутке, а функция g(x) убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более одного корня на этом промежутке. Если в уравнении f(x) = а функция f(x) возрастает или убывает на некотором промежутке, то это уравнение может иметь не более одного корня на этом промежутке. Решить уравнение - это значит найти все его корни или показать, что корней нет. Таким образом, уравнение 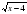 =
=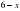 может иметь только один корень, который ищем подбором х=5.
может иметь только один корень, который ищем подбором х=5.
Рассмотрим уравнение 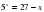
ОДЗ:  . Та же ситуация. Левая часть – возрастающая функция, правая - убывающая. Подбором находим х=2.
. Та же ситуация. Левая часть – возрастающая функция, правая - убывающая. Подбором находим х=2.
Вывод: эти уравнения решались, используя возрастание и убывание функций.
Рассмотрим уравнение 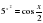
Проведем оценку левой и правой частей.
Левая часть: 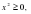
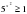 .
.
Правая часть:-1 .
.
Если в процессе решения выяснилось, что одна часть , а другая
, а другая , то равенство левой и правой частей возможно тогда и только тогда, когда л.ч. и п.ч. равны
, то равенство левой и правой частей возможно тогда и только тогда, когда л.ч. и п.ч. равны  одновременно. Значит, данное уравнение равносильно системе:
одновременно. Значит, данное уравнение равносильно системе:
Решаем первое уравнение системы:  ; х=0. Подстановкой убеждаемся, что х=0 подходит и ко второму уравнению соs0 =1. Ответ: 0
; х=0. Подстановкой убеждаемся, что х=0 подходит и ко второму уравнению соs0 =1. Ответ: 0
Вывод: при решении этого уравнения мы применяли оценку левой и правой частей уравнения.
Рассмотрим уравнение  .
.
Найдем ОДЗ этого уравнения:

Т.е, ОДЗ состоит из одного числа - 1. В этом случае, если уравнение и имеет решение, то только х=1. Проверкой убеждаемся, что х=1 корень данного уравнения.
Вывод: если ОДЗ состоит из конечного числа значений, то для решения достаточно проверить все эти значения непосредственной подстановкой. Иногда знание ОДЗ позволяет доказать, что уравнение не имеет решений.
(10 мин)
6. Первичное закрепление новых знаний.
Работа в группах. Задания одинаковые для всех групп. Определить способ решения данного уравнения (можно предложить найти корни той группе, которая справится с заданием быстрее)
1). (Решение: исследование на возрастание, убывание функций. Подбором находим х=1.)
(Решение: исследование на возрастание, убывание функций. Подбором находим х=1.)
2). = -
= -  ( Решение: оценка левой и правой частей. Левая часть
( Решение: оценка левой и правой частей. Левая часть  , а правая
, а правая  0. Корень уравнения х=4)
0. Корень уравнения х=4)
3). (Решение: конечная ОДЗ.
(Решение: конечная ОДЗ. . Корень уравнения х=3)
. Корень уравнения х=3)
4).  ( Решение: Левая часть убывающая функция на множестве R ( как сумма двух убывающих функций), а правая – постоянная.
( Решение: Левая часть убывающая функция на множестве R ( как сумма двух убывающих функций), а правая – постоянная.
Подбором находим х=2) (7 мин)
7.Практическое применение полученных знаний.
Задание для групп: Решить уравнение. У доски практики защищают одно из уравнений, которое им досталось в процессе жеребьевки.
1.
Решение: Находим ОДЗ:  ОДЗ:
ОДЗ: Конечная ОДЗ. Проверкой находим корень х = -1 Ответ: -1
Конечная ОДЗ. Проверкой находим корень х = -1 Ответ: -1
2. 
Решение: Поделим левую и правую части на 30 . Получим,
. Получим, или
или  . Левая часть убывающая функция на множестве R (как сумма двух убывающих функций), а правая – постоянная.
. Левая часть убывающая функция на множестве R (как сумма двух убывающих функций), а правая – постоянная.
Значит, уравнение имеет один корень. Подбором находим х=0. Ответ: 0.
3. 
Решение: ОДЗ: .
.  . Левая часть функция возрастающая на ОДЗ, а правая – убывающая на ОДЗ. Значит, уравнение может иметь только один корень. Подбором находим х=1. Ответ: 1
. Левая часть функция возрастающая на ОДЗ, а правая – убывающая на ОДЗ. Значит, уравнение может иметь только один корень. Подбором находим х=1. Ответ: 1
4. 
Решение: С помощью равносильных преобразований запишем уравнение в виде:  . Проведем оценку левой и правой частей уравнения. Левая часть
. Проведем оценку левой и правой частей уравнения. Левая часть  , а правая часть
, а правая часть 0. Равенство между левой и правой частями возможно только в том случае, если они одновременно равны 0. Таким образом, уравнение равносильно системе:
0. Равенство между левой и правой частями возможно только в том случае, если они одновременно равны 0. Таким образом, уравнение равносильно системе:

 . Решим первое уравнение. Сумма двух неотрицательных функций может равняться нулю тогда и только тогда, когда каждое из слагаемых равно нулю. Таким образом, получаем, что первое уравнение имеет единственный корень х=0. Это решение удовлетворяет и второму уравнению. Значит, уравнение
. Решим первое уравнение. Сумма двух неотрицательных функций может равняться нулю тогда и только тогда, когда каждое из слагаемых равно нулю. Таким образом, получаем, что первое уравнение имеет единственный корень х=0. Это решение удовлетворяет и второму уравнению. Значит, уравнение 
имеет единственный корень х=0. Ответ: 0 (11 мин)
7.Подведение итогов урока.
1).Выставляются оценки .
2). Учитель предлагает закончить предложения:
Мне понравилось…
Мне не понравилось…
Самым сложным для меня было…
Группа справилась с заданием потому, что…
8. Домашнее задание.
Составить четыре уравнения, которые решаются с помощью свойств функций.
Учитель: Мы рассмотрели нестандартные приемы решений уравнений. Я думаю, что вы убедились в том, что умение анализировать создавшуюся ситуацию, может во много раз ускорить процесс разрешения, казалось бы, не решаемой проблемы. (5 мин)

 Получите свидетельство
Получите свидетельство Вход
Вход



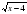 =6-x, способом возведения обеих частей в квадрат. (7 мин) 4. Актуализация опорных знаний.
=6-x, способом возведения обеих частей в квадрат. (7 мин) 4. Актуализация опорных знаний.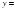
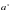 ; 2)
; 2) 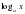 ; 3)
; 3) 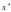 ; 4)
; 4) 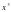 ; 5)
; 5)  ; 6)
; 6)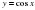 ; 7)
; 7) 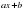 .
. 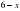
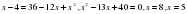 . Проверкой убеждаемся, что х=8 - посторонний корень. Ответ: 5
. Проверкой убеждаемся, что х=8 - посторонний корень. Ответ: 5 4. По теореме о корне, если в уравнении f(x)=g(x) функция f(x) возрастает на некотором промежутке, а функция g(x) убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более одного корня на этом промежутке. Если в уравнении f(x) = а функция f(x) возрастает или убывает на некотором промежутке, то это уравнение может иметь не более одного корня на этом промежутке. Решить уравнение - это значит найти все его корни или показать, что корней нет. Таким образом, уравнение
4. По теореме о корне, если в уравнении f(x)=g(x) функция f(x) возрастает на некотором промежутке, а функция g(x) убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более одного корня на этом промежутке. Если в уравнении f(x) = а функция f(x) возрастает или убывает на некотором промежутке, то это уравнение может иметь не более одного корня на этом промежутке. Решить уравнение - это значит найти все его корни или показать, что корней нет. Таким образом, уравнение 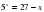
 . Та же ситуация. Левая часть – возрастающая функция, правая - убывающая. Подбором находим х=2.
. Та же ситуация. Левая часть – возрастающая функция, правая - убывающая. Подбором находим х=2. 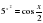
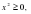
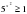 .
.








 Урок математики "Применение свойств функции при решении уравнений" (86.1 КB)
Урок математики "Применение свойств функции при решении уравнений" (86.1 КB)
 0
0 754
754 44
44 Нравится
0
Нравится
0


