Получите свидетельство
Вход
Лабиринт вопросов сложных
Разгадать помогут нам
Наши знанья и уменья
Со смекалкой пополам!
Цели урока: получить алгоритмы умножения дробей, умножения дроби на натуральное число и тренировать способность к их практическому использованию.
Обучающие
Систематизация знаний по теме дроби;
Формулирование правила умножения обыкновенной дроби на натуральное число, правила умножения обыкновенных дробей;
Отработка у обучающихся навыков применения правил при решении.
Развивающие:
Развитие аналитического мышления учащихся;
Формирование умения выделять главное и обобщать;
Развитие грамотной математической речи в ходе решения примеров;
Развитие навыков анализа и синтеза при выводе правила умножения
Воспитывающие:
воспитание интереса к математике, активности, творчества;
Воспитание аккуратности при выполнении математических записей.
Тип урока: урок изучения и первичного закрепления новых знаний.
Применяемая технология – проблемно-диалоговая
Этапы урока:
Актуализация знаний.
Усвоение нового материала
Первичная проверка понимания.
Подведение итогов на рефлексивной основе
Домашнее задание.
Ход урока.
I. Организационный этап.
Добрый день, ребята. Эпиграфом к нашему уроку будут эти строки: Лабиринт вопросов сложных разгадать помогут нам наши знанья и уменья со смекалкой пополам!
Сегодня, изучая новую тему, мы, может быть, и не сделаем великих открытий, но значимые для себя открытия вы совершите обязательно. Для этого надо быть настойчивым и внимательным.
II. Этап актуализации знаний.
Цели:
Актуализация опорных знаний, необходимых для введения и обоснования правила.
Создание ситуации успеха для последующей деятельности.
Графический диктант
Графический диктант
Ответ «Да» соответствует
ответ «нет» соответствует
Для тех, кто закончил раньше. В четырех словах переставили буквы.
Вот что получилось:
ХАМУ, АСО, ЛЕЧПА, ЛОСН
Какие это слова и какое слово здесь лишнее?
Самопроверка. Сравните ваши ответы с ключом для задания и правильный ответ обведите кружочком, у вас должна получиться цепочка. Поднимите руки те, у кого цепочка не оборвалась? Поставьте себе отметку «5». Теперь поднимите руки те, у кого получилась рваная цепочка? В каком месте произошел обрыв? Вспомним правило, по которому мы выполняем это задание. ( Разбор ошибок)
III. Этап мотивации.
Цель:
формирование у каждого ученика личной потребности в последующей деятельности, связанной с открытием нового правила.
- Откройте тетради, запишите число.
Какие действия с дробями вы умеете выполнять и знаете правило, как это сделать?
( Действия с дробями. Мы умеем сравнивать, складывать, вычитать дроби с разными знаменателями и эти же действия со смешанными числами.)
- Как вы думаете, что еще необходимо изучить, чтобы в полной мере оперировать с дробями?
( Умножение и деление дробей.)
- Сегодня на уроке будем работать над темой: “Умножение дробей”. (Записывают тему в тетрадь).
IV. Этап постановки учебной задачи.
Цель:
непосредственное подведение обучающихся в необходимости «открытия нового правила».
- Какова же цель сегодняшнего урока : …. (открыть (вывести , получить, узнать) правило умножения обыкновенных дробей (как умножаются обыкновенные дроби)).
И кто нам в этом поможет? (учитель, учебник)
V. Этап моделирования правила.
Цель:
создание модели правила, ее анализ и уточнение
Предлагаю вам решить задачу: Котенок утром, днем и вечером съел по 2/3 сосиски. Сколько сосисок съел котенок за день? Как узнать ответ на вопрос?
( сосиски).
- Что значит умножить число а на число в?
( надо взять число а слагаемым b раз). А как по-другому можно решить эту задачу?
Какой ответ получим? Кто догадался, как умножить дробь на натуральное число?
( предлагают свои гипотезы)
Так как это гипотеза, то она нуждается в проверке. Как будем проверять?
( По учебнику)
Работа с текстом учебника стр. 68 - 69.
Задача для учащихся – научиться умножать обыкновенные дроби на натуральное число.
- По какому алгоритму выполняется умножение обыкновенной дроби на натуральное число?
1 шаг – умножить натуральное число на числитель дроби
2 шаг – если это возможно, сократить
3 шаг – перемножить числа после сокращения, знаменатель оставить тем же.
Чья гипотеза была правильной?
VII. Этап первичной проверки понимания правила.
- Теперь каждый из вас составит пример на это правило и запишет его на доске.
- Вы составили для себя самостоятельную работу. Какие правила нужно знать, чтобы успешно справиться с работой? (правило умножения дроби на число и правило сокращения дробей)
( решают примеры)
Проверка.
- С какой целью вы выполняли это задание? Как будем оценивать? Дадим право на ошибку?
( оценивают работу)
- Какие отметки вы себе поставили? Почему?
- А сейчас проведем гимнастику для глаз.
Упражнения для глаз
Будем делать мы сейчас.
Смотрим вверх и смотрим вниз.
Смотрим вдаль и смотрим вблизь.
И десяток раз моргнем,
И зажмуримся потом.
Если глазки устают –
Упражнения спасут!
VII. Этап моделирования правила.
Какую цель мы ставили в начале урока? Достигли ее? (Нет.)
- Почему? ( А если две дроби надо перемножить?)
- Приведите пример.
- А здесь как поступим? (предлагают правило) Проверим?
Работа с текстом учебника стр. 68 - 69.
Задача для учащихся – научиться перемножать обыкновенные дроби.
- По какому алгоритму выполняется умножение обыкновенных дробей?
1 шаг – умножить числитель первой дроби на числитель второй дроби, знаменатель первой дроби на знаменатель второй
2 шаг – если возможно, сократить дроби
3 шаг – выполнить умножение числителей и знаменателей.
VIII. Этап первичной проверки понимания правила.
- Сейчас каждый из вас составит пример на это правило и запишет его на доске.
- Вы составили для себя самостоятельную работу. Какие правила нужно знать, чтобы успешно справиться с работой? (правило умножения обыкновенных дробей и правило сокращения дробей)
(решают примеры)
Проверка.
- С какой целью вы выполняли это задание? Как будем оценивать? Дадим право на ошибку?
(оценивают работу)
- Какие отметки вы себе поставили? Почему?
Весь материал - в документе.
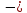Ключ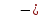 
= 
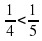
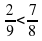
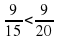
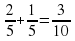
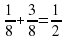
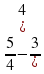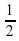
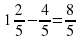
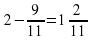
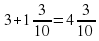
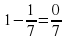
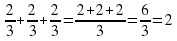( сосиски).
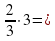(2)
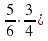
Урок математики по теме "Умножение обыкновенных дробей" (29.37 КB)
0
1685
368
Нравится
0
