Обучающие цели урока Знать правило деления обыкновенных дробей, свойства деления. Применять полученные знания при решении заданий.
Развивающие цели позволяют
-развивать познавательный интерес учащихся
-формировать вычислительную культуру учащихся
- развивать логическое мышление, то есть формировать умение наблюдать, выявлять закономерности, сравнивать и сопоставлять, проводить дедуктивные умозаключения и умозаключения по аналогии
Воспитательные цели. Ученик осознанно перерабатывает полученные знания для выработки целостной системы знаний по данной теме
формирует умения, организующие деятельность: ставить цели и задачи, определять способы их реализации, планировать свои действия, реализовать действия и проверить результат
развивает самостоятельность и добросовестность введением игровой ситуации снимает напряжение на уроке
Формы работы учащихся: фронтальная, индивидуальная, групповая(в парах)
Необходимое техническое оборудование: доска, проектор, компьютер.
Структура и ход урока
1. Организационный момент (3 мин)
Приветствие учителя, проверка готовности учащихся и классного помещения к проведению урока.
История
2. Мотивация учащихся (1 мин)
3.Актуализация опорных знаний.(15 мин)
4. Знакомство с новым материалом (15 мин)
5. Физминутка (1 мин)
6. Подведение итогов (5 мин)
7. Ррефлексия (2 мин)
8. Выставление оценок ( 3 мин)
Ход урока
1. Организационный момент.1 мин
Поэт Сеф писал вот такие замечательные слова:
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Из истории математики 2 мин
Хотя умножение в старину считалось очень нелегким делом (мало кто знал тогда таблицу умножения), но деление было еще сложнее. В Италии до сих пор сохранилась поговора: «Трудное дело деление». Так говорят, когда оказываются перед почти неразрешимой проблемой. В средние века людей, умеющих производить деление, можно было пересчитать по пальцам. Они переезжали из города в город по приглашению купцов, желавших привести в порядок свои счета.
Методов деления было придумано немало. Монах-математик Герберт, будущий Папа Римский Сильвестр II, привел несколько способов. Но они были настолько сложны, что их не понимали даже самые прилежные ученики. Один из этих способов так и назвали «железное деление»
2. Мотивация урока. 1 мин
Дроби всякие нужны,
Дроби разные важны.
Дробь учи,
Тогда придет к тебе удача.
Коли будешь дроби знать
Точный смысл их понимать,
Станет легкой
Даже трудная задача.
3.Актуализация опорных знаний. 15 мин
За каждый правильный ответ получают жетоны
1. Чтобы умножить дробь на дробь, надо …
2. Какие числа называются взаимно обратные
Устный счет 5
ЗАДАНИЕ :Раздать карточки таблица умножения
|
А |
Б |
В |
Г |
Д |
Е |
|
6 × 3 |
4 × 5 |
3 × 7 |
72 : 8 |
15 : 3 |
12 : 6 |
|
8 × 2 |
6 × 7 |
8 × 8 |
14 : 2 |
0 : 9 |
54 : 9 |
|
5 × 4 |
7 × 9 |
3 × 5 |
27 : 3 |
64 : 8 |
14 : 7 |
|
9 × 7 |
8 × 3 |
8 × 10 |
30 : 6 |
16 : 8 |
80 : 8 |
|
8 × 0 |
7 × 7 |
6 × 6 |
90 : 9 |
35 : 7 |
45 : 5 |
|
4 × 6 |
9 × 8 |
5 × 2 |
32 : 4 |
81 : 9 |
18 : 6 |
|
3 × 8 |
7 × 2 |
7 × 6 |
54 : 6 |
12 : 4 |
36 : 9 |
|
8 × 5 |
9 × 2 |
9 × 9 |
25 : 5 |
40 : 5 |
16 : 2 |
|
6 × 10 |
5 × 3 |
0 × 7 |
56 : 7 |
21 : 7 |
20 : 4 |
|
3 × 4 |
6 × 9 |
6 × 2 |
18 : 3 |
45 : 9 |
48 : 6 |
Учитель: сегодня на уроке мы изучим новую тему: Деление дробей. Мы должны научиться делить дроби, применять деление дробей при решении примеров и задач. Давайте все вместе сочиним сказку. Как начинаются большинство сказок? Появляется Флипчпарт с текстом «сказки»: Жили–были обыкновенные дроби. Были они правильные и неправильные, а также смешанные, сократимые и несократимые, а ещё взаимно обратные. Жили они дружно и научились выполнять различные действия. Какие?
Какие действия с обыкновенные дробями вы умеете выполнять ? (сложение, вычитание, умножение)
Появляется следующий слайд
Учащиеся открывают тетради и решают в них три примера на сложение, вычитание и умножение.
У доски решают примеры 3 учащихся.
Первые учащиеся, кто решил задания получают жетоны
ЗАДАНИЕ : Назовите взаимно обратные числа
4. Объяснение нового материала
Как найти ширину прямоугольного участка, если известны длина и площадь?
Ответ учащихся: Что бы найти ширину надо площадь разделить на длину.
Тему урока «Деление дробей» записать на доске и в тетрадях. На доске записана краткая запись задачи:
Площадь участка – 5/7 кв.км
Длина участка – 3/4 км
Ширина участка –?
Решение задачи.
Пусть ширина участка будет х км.
Уравнение: 3/4х = 5/7
На какое число нужно умножить 3/4х, чтобы получить х, то есть, на сколько надо умножить 3/4, чтобы получить 1? (На 4/3)
4/3*3/4х = 5/7 х = 5/7*4/3
Вопросы учащимся:
2) На какое действие заменили деление?
3) Что изменилось? Что не изменилось?
4) 3/4 и 4/3. Как называются эти числа?
Сформулировать правило деления дробей. Откройте учебник на странице 208, прочитайте правило деления дробей по учебнику. Учащиеся первого варианта рассказывают это правило учащимся второго варианта. Кто получил правильный ответ?
(Проводится физкульминутка)
Записать в тетрадь
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
И решили все в царстве дробей, что теперь их жизнь будет лучше, но правило это надо было научиться применять.
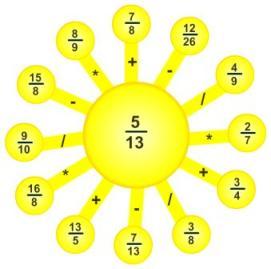
Все в тетрадях выполняют № 794(1,3,5,7)
Первые, кто решат правильно указанные примеры, получают по одному жетону за каждый верно выполненный пример.
Учитель.
У меня к вам есть несколько вопросов, но из царства обыкновенных дробей сорока на хвосте принесла, что вы устали.
И решили дроби в честь такого знаменательного события устроить праздник. Пропуском на праздник будут служить ваши жетоны
Подведение итогов.
- Сколько жетонов собрали. Вы тему урока усвоили.
5. Домашнее задание: упр. № 794(2,4,6,8)
6. Подведение итогов Флипчпрт
- Математический диктант «Да - Нет».
Каждый получает 8 вопросов: если утверждение верно - ставят «+», если неверно «-». Затем – сверка результатов. Максимальная оценка за это задание 8 баллов
- Число, записанное над чертой дроби, называется числителем.
- Чтобы найти дробь от числа, надо число разделить на дробь.
- Правильная дробь - это дробь, у которой числитель меньше знаменателя.
- Неправильная дробь меньше 1.
- Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
- Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители и знаменатели.
- Чтобы умножить две дроби, надо умножить их числители и знаменатели.
- Чтобы выполнить деление обыкновенных дробей, нужно делимое умножить на дробь обратную делителю.
Затем поменяться тетрадями и проверить друг у друга
7. Рефлексия.
- Что узнали для себя нового?
- Что заинтересовало? Почему?
- Проанализируйте свою работу на каждом этапе.
- Что показалось интересным?
- Что самое главное и что надо запомнить?
8. Выставление оценок. Дополнительное задание.
В архиве анализ урока и дополнительные задания.

 Получите свидетельство
Получите свидетельство Вход
Вход




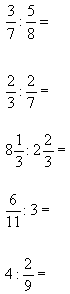










 Деление обыкновенных дробей (0.27 MB)
Деление обыкновенных дробей (0.27 MB)
 0
0 1331
1331 156
156 Нравится
0
Нравится
0






