Урок математики по теме «Формулы сокращенного умножения: разность квадратов» (7 класс).
Цель урока:
Для учителя:
Создать условия для вывода учащимися формулы сокращенного умножения 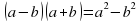 , посредством организации групповой работы.
, посредством организации групповой работы.
Формировать умение применять данную формулу для преобразования алгебраических выражений.
Для учащихся:
Определить способ сокращенного умножения разности выражений на их сумму.
Учиться выявлять случаи применения формулы сокращенного умножения 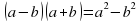 и пользоваться ею для упрощения выражений.
и пользоваться ею для упрощения выражений.
Развивающий аспект: Развитие мышления (умение синтезировать, анализировать и обобщать рабочий материал).
Воспитательный аспект: Развитие коммуникативных способностей (умение выслушать точку зрения другого, умение прийти к общему мнению).
Формы организации деятельности учащихся:
Индивидуальная;
Работа в парах;
Групповая;
Фронтальная.
| № | Этапы урока, время | Деятельность учителя | Деятельность обучающихся | Доска и оборудование |
| 1. | Организационный момент (1 мин.). | Приветствует учащихся. Проверяет готовность обучающихся к уроку. | Выполняют записи в тетради. | Записываем на доске: |
| 2. | Актуализация знаний (3 мин.). | Проводит устную работу с классом. -Прочитайте выражение: 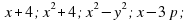
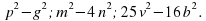
-Возведите в квадрат следующие одночлены: 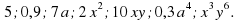
| Желающие дать ответ отвечают с места. | На доске записаны задания для устной работы. |
| 3. | Открытие нового знания (10 мин.). | - Сейчас я дам вам задание, которое вы будете выполнять в группе, оно состоит из двух частей: На этом этапе учитель: Делит класс на группы. Раздает группам карточки – задания (задания в приложении). Объясняет классу задачу работы в группе. Контролирует работу в группах. Создает условия для продуктивной межгрупповой коммуникации. Диалог с выступающими у доски: -Заметили ли вы закономерность при выполнении задания?
| Учащиеся в группах распределяют функции между всеми учащимися. Выполняют задание. Готовят решение на доске. Сообщают о своих результатах и выводах другим группам. В общем обсуждении выводят новую формулу.
-Заметили. Если сумму одночленов умножить на разность этих же одночленов, то получится разность квадратов этих одночленов. | Детям раздаются карточки с заданиями. Учащиеся в тетрадях выполняют задание. Доска приготовлена для фиксации группами своих результатов.
|
| 4. | Формулирование цели и темы урока(2 мин.). | -Какой вывод можно сделать в результате выполнения задания?
-Давайте проверим правильность нашего определения обратившись к учебнику. -Как вы думаете, какую цель урока мы можем поставить?
-Верно. Тогда как может звучать тема нашего урока? -Давайте запишем тему урока в тетрадь. | -Вывод: 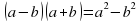 . .
Читают необходимое утверждение в учебнике.
-Научиться «узнавать» случаи, в которых применяется эта формула. -Научиться применять новую формулу. -Применение формулы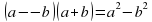 . . Записывают тему в тетрадь. | Работа с учебником. Запись в тетради и на доске темы урока. Фиксируем на доске цели урока. |
| 5. | Первичное применение нового знания (15 мин.). | -Мы с вами получили новую формулу, и я хочу вам предложить попробовать применить ее. Раздает карточки – задания для закрепления материала. Карточка. Составьте из данных выражений все возможные тождества: (1 +a)(1 – a); (y – 3)(y +3); 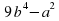 ; ;
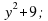
(3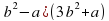 ; ; 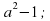
(3-y)(3+y); 9 -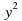 . . Выберете алгебраические выражения, которые могут быть преобразованы по формуле произведения суммы на разность, и преобразуйте их по этой формуле: 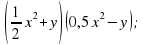
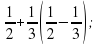
(x – y) – (x + y); (0,2 – x)(0,2 – x); (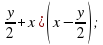 (c – ab)(c + ab); 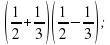
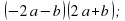
((-2a) – b)((-2a) +b); 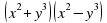 . .
Ответьте на вопросы: Влияет ли порядок записи слагаемых в множителе – сумме на результат преобразования по формуле 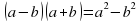 ? ? Влияет ли порядок записи выражений, входящих в разность, на результат преобразования по этой формуле? По какому множителю (по сумме или по разности) удобно записывать правую часть формулы? Важен ли порядок действий в произведении? Комментирует текст заданий. Обсуждает с учащимися результаты работы с тренировочными заданиями.
|
Первое задание на карточке учащиеся выполняют в тетради самостоятельно. Ученик, справившийся с заданием первым, фиксирует на доске решение.
Второе задание учащиеся выполняют самостоятельно. На вопросы отвечают парах. Одна пара работает у доски (пара выполняет задание на доске, скрытой от класса до момента обсуждения). Затем учащиеся сверяют свои результаты работы с зафиксированными результатами на доске. В общей беседе находят верные ответы на вопросы, поставленные в тренировочном задании. | Детям раздаются карточки с заданиями. Работа в тетрадях. Фиксация результатов работы на доске. |
| 6. | Самостоятельная работа (9 мин.). | -После того, как мы с вами выяснили как применяется формула 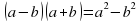 , я хочу вам предложить самостоятельно выполнить несколько заданий. , я хочу вам предложить самостоятельно выполнить несколько заданий. Раздает учащимся карточки – задания (задания в приложении). -Теперь поменяйтесь тетрадями и проверьте работу вашего соседа по парте по готовым ответам на доске. 2. Открывает доску, на которой записаны ответы к заданиям. -За три верных задания – оценка «3», за четыре верных задания – оценка «4» и все верные задания оцениваются на «5». 3. Подводит итог об уровне усвоения изученного материала. | Самостоятельно выполняют задание. Меняются тетрадями и проверяют работу друг друга по приготовленным ответам на задания. Выставляют оценку. | Работа в тетрадях. Фиксация на доске ответов к самостоятельной работе. |
| 7. | Итог урока (3 мин.). | - Ребята, какие цели сегодня на уроке были нами поставлены?
-Мы достигли поставленных целей? | По зафиксированным записям на доске ребята отвечают: -Научиться «узнавать» случаи, в которых применяется эта формула. -Научиться применять новую формулу. - Да, достигли. -Не у всех еще получается. -Дома нужно еще закрепить. | Работа с доской. |
| 8. | Домашнее задание(2 мин.). | Выдает домашнее задание. | Записывают домашнее задание в дневники. | Работа с дневниками. |
Приложение.
Задания к третьему этапу урока «Открытие нового знания».
Карточки – задания.
1 группа.
Выполните умножение:
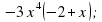
(3 – a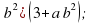
(3a + b)(a – 3b);
(a + b)(a – b);
(3x – 2y)(3x + 2y);
(6a + 2b)(6a – 2b).
Заметили ли вы какую – либо закономерность работая с данными произведениями?
Вывод:
2 группа.
Выполните умножение:
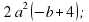
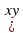 − 2)(xy +2);
− 2)(xy +2);
(6a – 8)(a – 8);
(d – c)(c +d);
(2c – d)(2c +d);
(7p – 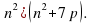
Заметили ли вы какую – либо закономерность работая с данными произведениями?
Вывод:
3 группа.
Выполните умножение:
6y(7 – d);
(2a + 3b)(2a – 3b);
(2x +n)(5x – 3);
(7x – 1)(1 +7x);
(5
(4
Заметили ли вы какую – либо закономерность работая с данными произведениями?
Вывод:
4 группа.
Выполните умножение:

 − 1)(3 +d);
− 1)(3 +d);
(2c +4)(4 – 2c);
(6 – 3x)(6 +3x);
(5
Заметили ли вы какую – либо закономерность работая с данными произведениями?
Вывод:
Задания к 6 этапу урока «Самостоятельная работа».
Карточки – задания.
Преобразуйте выражения по формуле:
В -1.
(5 -3y)(5 +3y);
(6x +y)(y – 6x);
(5x – 8b)(5x + 8b);
(1 – 4 )(4
)(4

(c – a)(c + a);
(7a + 10b)(10b – 7a);
(3x – 1)(1 +3x);
(x – 9)(9 + x);
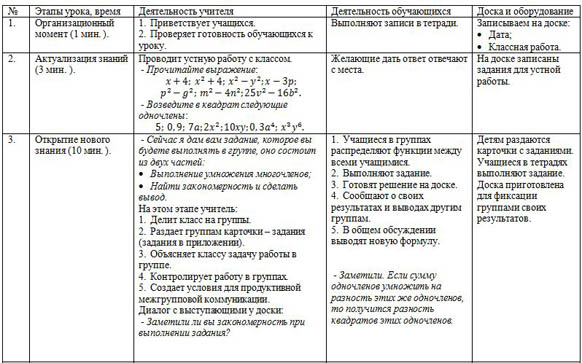
6

 Получите свидетельство
Получите свидетельство Вход
Вход



 , посредством организации групповой работы.
, посредством организации групповой работы.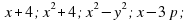
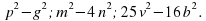
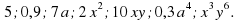
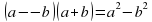 .
.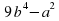 ;
;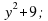
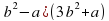 ;
;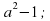
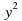 .
.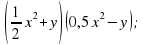
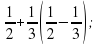
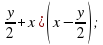
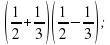
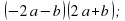
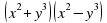 .
.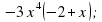
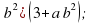
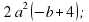
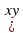 − 2)(xy +2);
− 2)(xy +2);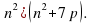









 Урок математики по теме «Формулы сокращенного умножения разность квадратов» (37.26 КB)
Урок математики по теме «Формулы сокращенного умножения разность квадратов» (37.26 КB)
 0
0 448
448 119
119 Нравится
0
Нравится
0


