Урок алгебры в 7 классе по теме:
«Формулы сокращенного умножения».
Учитель математики Мелитопольской общеобразовательной школы I – III ступеней № 11
Авотин Игорь Олегович
Цель урока:
Разобрать совместно с учениками формулы квадрата суммы двух выражений, квадрата разности двух выражений и разность квадратов двух выражений. Рассмотреть геометрический смысл формул сокращенного умножения. Закрепить полученные знания в ходе выполнения заданий с использованием сервиса http://learningapps.org/ , карты знаний.
В результате ученик должен знать:
Формулы квадрата суммы и квадрата разности двух выражений, формулу разности квадратов двух выражений.
Словесную и символьную записи этих формул.
Геометрический смысл данных выражений.
Значение данных формул в преобразовании многочленов и сокращении алгебраических дробей.
Ход урока:
I Организационный момент.
Здравствуйте, ребята. Тема нашего урока формулы сокращённого умножения, как вы думаете, судя по названию для чего нужны эти формулы?
II Изучение нового материала.
Квадрат суммы
Рассмотрим квадрат со стороной a+b . Его площадь равна 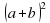 Но этот квадрат мы разделили на четыре части (слайд 6): квадрат со стороной а (его площадь равна
Но этот квадрат мы разделили на четыре части (слайд 6): квадрат со стороной а (его площадь равна 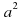 ), квадрат со стороной b ( его площадь равна
), квадрат со стороной b ( его площадь равна 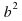 ), два прямоугольника со сторонами a и b (площадь каждого такого прямоугольника равна ab)(слайд 7). Значит
), два прямоугольника со сторонами a и b (площадь каждого такого прямоугольника равна ab)(слайд 7). Значит 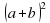 =
=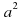 +
+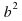 +2ab, т.е. получили формулу квадрата суммы
+2ab, т.е. получили формулу квадрата суммы 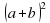 =
=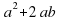 +
+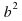 (слайд 8-10)
(слайд 8-10)
Полученное тождество 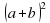 =
=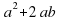 +
+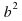 называется формулой квадрата суммы. (слайд 11)
называется формулой квадрата суммы. (слайд 11)
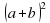 =
=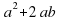 +
+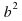 Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого на второе, плюс квадрат второго выражения. (слайд 12)
Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого на второе, плюс квадрат второго выражения. (слайд 12)
Рассмотрим пример: ( слайды 13-15)
Раскройте скобки в выражении
(3x + 4ky)2 =9x 2 +24xky + 16k2y2
Возведем в квадрат сумму 7n + 4m
По формуле квадрата суммы получим:
(7n + 4m)2 = (7n)2 + 2 × 7n × 4m + (4m)2= 49n2 + 56nm + 16m2 (слайд 16)
Раскройте скобки в выражениях: (слайд 17)
1) (3 + 8р)2 = 64р2 + 48р + 9
2) ( 6х + 4)2 = 36х2 + 48х + 16
3) (4,2 + 0,5х)2 =0,25х2+4,2х+17,64
4) (0,3ху+k)2 =0,09х2у2+0,6хуk+k2
Квадрат разности (слайд 15)
Возведем в квадрат разность 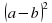 ) = (a – b)(a – b) = …Закончите преобразование (слайд 16)
) = (a – b)(a – b) = …Закончите преобразование (слайд 16)
Полученное тождество (a – b)2 = a2 – 2ab + b2 Называется формулой квадрата разности.
(слайд 17)
Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого на второе, плюс квадрат второго выражения. (слайд 18)
Рассмотрим пример: ( слайды 19 - 21)
Раскройте скобки в выражениях: (слайд 20)
1) (5х-3)2 =25х2 – 30х + 9
2) (13-6р)2 =36р2–156р+169
3) (2,3-0,4х)2 =0,16х2–1,84х+5,29
4) (0,6ху-k)2 =0,36х2у2–1,2хуk+k2 (слайд 21)
Разность квадратов (слайд 22)
Пусть a и b – положительные числа, причем ab. Рассмотрим прямоугольник со сторонами a+b и a-b (слайд 23). Его площадь равна (a+b)( a-b) (слайд 24). Площадь получившейся фигуры та же. Данную фигуру можно рассматривать так: из квадрата со стороной а вырезать квадрат со стороной b , значит площадь новой фигуры равна 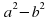 (слайд 25)
(слайд 25)
Получим a2 – b2 = (a – b)(a + b) (слайд 26). Формула разности квадратов
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. (слайд 28-31)
Рассмотрим пример: ( слайды 32 - 34)
Разложите на множители
16х8 – 9 ( подсказка 16х8 = (4х4)2 )
(a – b)(a + b) = a2 – b2
Это тождество позволяет сокращенно выполнять умножение разности любых двух выражений на их сумму.
Выполните умножение выражений
(k–c)(k+c) = k2 – c2
(4f+3)(4f–3) = 16f 2– 9
(5d–7b)(5d+7b) = 25d2– 49b2
III Закрепление материала ( слайд 35 - 37) – Викторина.
Задание
Необходимо выбрать соответствие между картинкой и определением формулы
Кто хочет стать миллионером?
Задания на проверку знания формул сокращенного умножения.
Скачки
Соревнование между учеником и ПК.
IV Итог урока – устный опрос.
1) Для чего нужны формулы сокращённого умножения?
2) Сформулируйте формулу квадрата суммы.
3) Запишите формулу квадрата суммы.
4) Сформулируйте формулу квадрата разности.
5) Запишите формулу квадрата разности.
6) Сформулируйте формулу разности квадратов.
7) Запишите формулу разности квадратов.


 Получите свидетельство
Получите свидетельство Вход
Вход



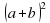 Но этот квадрат мы разделили на четыре части (слайд 6): квадрат со стороной а (его площадь равна
Но этот квадрат мы разделили на четыре части (слайд 6): квадрат со стороной а (его площадь равна 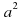 ), квадрат со стороной b ( его площадь равна
), квадрат со стороной b ( его площадь равна 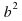 ), два прямоугольника со сторонами a и b (площадь каждого такого прямоугольника равна ab)(слайд 7). Значит
), два прямоугольника со сторонами a и b (площадь каждого такого прямоугольника равна ab)(слайд 7). Значит 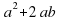 +
+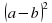 ) = (a – b)(a – b) = …Закончите преобразование (слайд 16)
) = (a – b)(a – b) = …Закончите преобразование (слайд 16)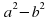 (слайд 25)
(слайд 25)








 Урок математики на тему "Формулы сокращенного умножения" (46.98 КB)
Урок математики на тему "Формулы сокращенного умножения" (46.98 КB)
 0
0 875
875 69
69 Нравится
0
Нравится
0


