Урок математики в 7 классе.
Подготовила учитель математики Умирбаева К.У.
Тема урока. Формулы сокращенного умножения.
Цель:
1. Образовательная: закрепить знания учащихся о формулах сокращенного умножения, сформировать умения применения формул при решении задач.
2. Развивающая: развить познавательный интерес к математике, логическое мышление, математическую речь, наблюдательность, умение систематизировать и применять полученные знания.
3. Воспитательная: воспитать ответственное, творческое отношение у учебному труду.
Тип урока: Урок обобщения и систематизация знаний.
Оборудование: мультимедиа, плакаты с формулами, раздаточный материал.
План урока.
Организационный момент, постановка цели урока.
Актуализация знаний «Верховая езда»
Проверка домашнего задания.
«Фехтование на шпагах» Тест на соотношение.
«Стрельба из пневматического пистолета»
«Плавание вольным стилем» Самостоятельная работа по уровням.
«Бег»
Работа с учебником.
Кроссворд
Дополнительное задание
Итоги урока. Рефлексия «Синквейн»
ХОД УРОКА
“У математиков существует свой язык – это формулы”.
С. Ковалевская
Организационный момент, постановка цели урока.
Здравствуйте, ребята! Сегодня я хотела бы начать урок отрывком из произведения «Автобиография» сербского писателя 19 века Нушича Бранислава:
«— Где ты родился, Спира? — спрашивает учитель математики Спиру Найдановича.
Спира молчит, хлопает глазами и смотрит в потолок.
— Где ты родился, Спира? — повторяет учитель.
Спира молчит, хлопает глазами и смотрит в потолок.
— Бог ты мой, ты что, не знаешь, где ты родился?
— Я забыл.
— А что же ты тогда знаешь? Ну, скажи мне, что ты знаешь, если ты даже не знаешь, где ты родился?
— А плюс В в квадрате равно А в квадрате плюс два АВ плюс В в квадрате! — выпаливает Спира, как из пулемета.».
Чем же этот отрывок связан с нашим уроком?
Сегодня у нас обобщающий урок по теме «Формулы сокращенного умножения», мы посмотрим, а как же мы выучили формулы сокращенного умножения и как же мы их можем применять. Откройте тетради, запишите число, классная работа, тему урока.
Проверка домашнего задания:
Проверить правильность в решении примера №273 стр 103
І.«Верховая езда»
Актуализация знаний. Закрепление домашнего знания.
Формулой называется символьная запись, содержащая некоторое утверждение.
а) При записи формул были допущены ошибки . Найдите и исправьте их.
1) (а²+в²) =а²+ав+в²
Ответ : (а+в)²=а²+2ав+в²
2) (а-с)²=а²-2ас+с²
Ответ : (а-в)²=а²-2ав+в²
3) (а+в)³=а³+а²в+ав²-в³
Ответ : (а-в)³=а³-3а²в+3ав²-в³
4) (а-в)³=а³-3ав+3ав-в³
Ответ : (а-в)³=а³-3а²в+3ав²-в³
5) а²-в²=(а-в)(а-в)
Ответ : а²-в²=(а-в)(а+в)
Некоторые правила сокращенного умножения были известны еще около 4 тысяч лет тому назад. Их знали вавилоняне и другие народы древности. Но в то время они формулировались словесно или геометрически.
Ни у древних Египтян, ни у древних вавилонян в алгебре не было букв. Буквами для обозначения чисел не пользовались и греческие учёные.
4. «Фехтование на шпагах» Тест на соотношение
Соединить линиями части верного равенства. За каждый верный ответ 1 балл. Всего – 6 баллов.
| 1) (4у + 3)2 = | 1) 4у2 – 28у + 49 |
| 2) (2у – 7)2 = | 2) 4у2 – 12х2у + 9х4 |
| 3) (1 – 3у)(1 + 3у) = | 3) у4 + 4х3у + 4х6 |
| 4) (2х – у)(у + 2х) = | 4) 16у2 + 24у + 9 |
| 5) (у2 + 2х3)2 = | 5) 1 – 9у2 |
| 6) (2у – 3х2)2 = | 6) 4х2 – у2 |
Ответы на тест:
| 1) (4у + 3)2 = | 4) 16у2 + 24у + 9 |
| 2) (2у – 7)2 = | 1) 4у2 – 28у + 49 |
| 3) (1 – 3у)(1 + 3у) = | 5) 1 – 9у2 |
| 4) (2х – у)(у + 2х) = | 6) 4х2 – у2 |
| 5) (у2 + 2х3)2 = | 3) у4 + 4х3у + 4х6 |
| 6) (2у – 3х2)2 = | 2) 4у2 – 12х2у + 9х4 |
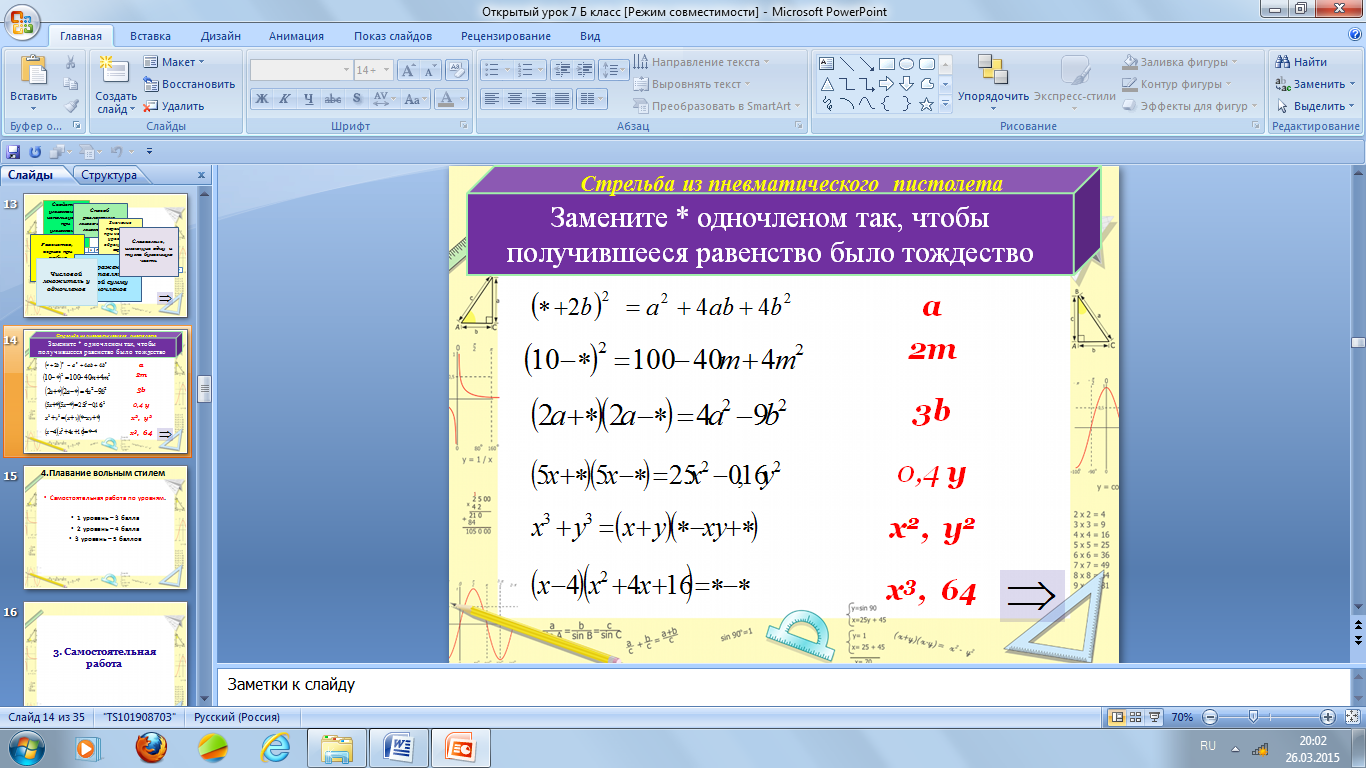
5. «Стрельба из пневматического пистолета»
6. «Плавание волным стилем» Самостоятельная работа по уровню успеваемости
1 уровень - 3 балла
2 уровень - 4 балла
3 уровень - 5 балла
№ 1. Представьте в виде многочлена
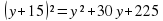
(n-4n³)(n+4n³)=n² - 16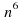
(-7x-1)² = -(7x²+1) = -( 49x² +14x + 1)= - 49x² -14x - 1
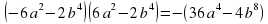
№ 2. Разложите на множители
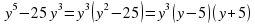
16x+8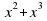 =x(16+8x+
=x(16+8x+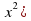
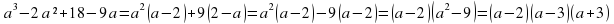
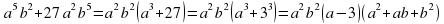
№ 3. Упростите выражение
(x+7)²-10x=x²+14x+49-10x= x²+4x+49
(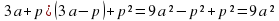
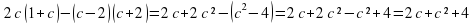
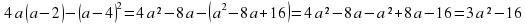
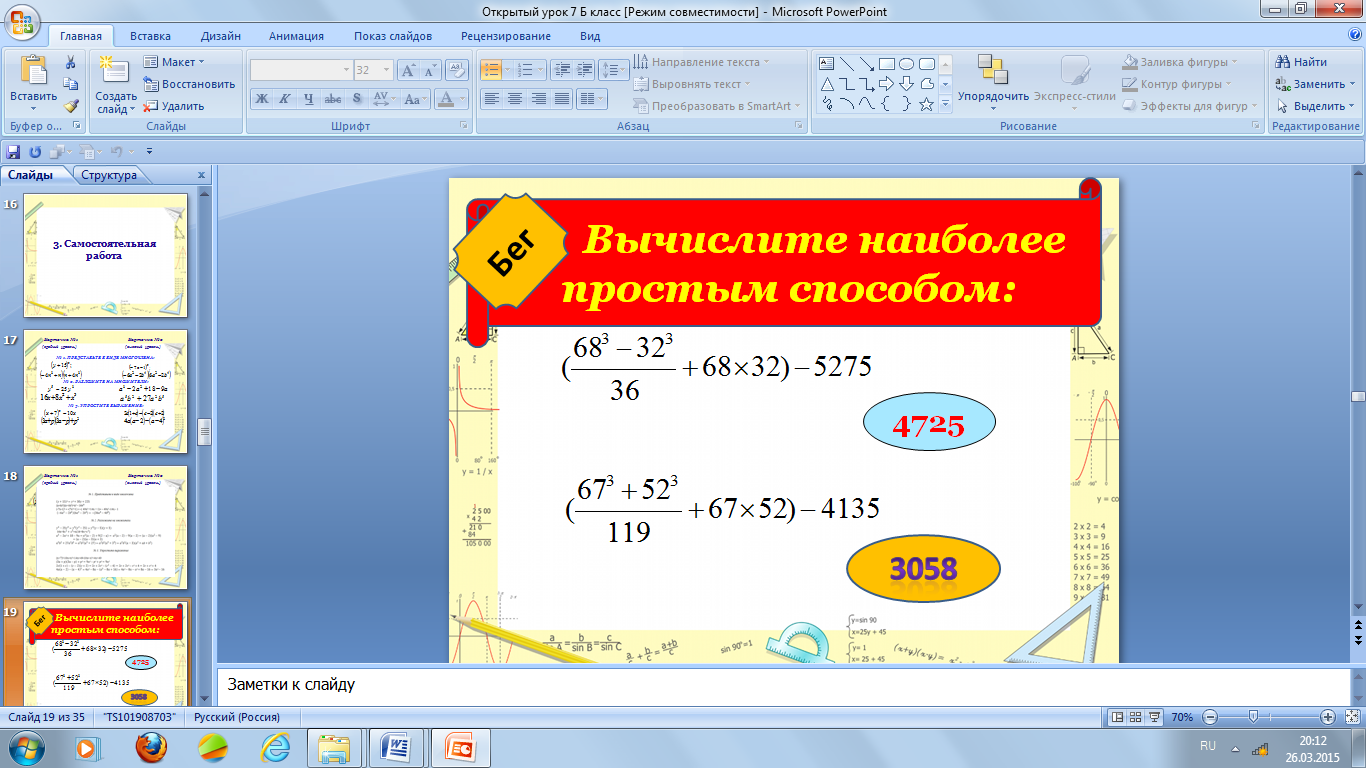
7. «Бег»
8. Физкультминутка
9. Практическая работа по учебнику № 276 (1-4) стр 104
10. Итог урока
a) по одному ученику самостоятельно выполняет задание на магнитной доске по карточке.
| (a + b)2 = | a2 + 2ab + b2 |
| (a – b)2 = | a2 – 2ab + b2 |
| a2 – b2 = | (a – b)(a + b) |
| a3 + b3= | (a + b)(a2 – ab + b2) |
| a3 – b3= | (a – b)(a2 + ab + b2) |
| (a + b)3 = | a3 + 3a2b + 3ab2 + b3 |
| (a – b)3 = | a3 – 3a2b + 3ab2 – b3 |
б) Самостоятельно выполняют задания. Отвечает ученик, работавший у доски. Ученики устно находят верное выражение и отвечают.
11. Рефлексия «Синквэйн»
1) одно слово, описывающее тему (существительное)
2) два слова, описывающие тему (прилагательное)
3 ) три слова, выражающие действия по теме (глагол)
Составить предложение по данным параметрам .
12.Домашнее задание:
Выполнить тест по теме «Формулы сокращённого умножения».
137 Оценивание
Критерий оценивания:
35-30 баллов - «5»
29 - 24 баллов - «4»
меньше 23 баллов - «3»
Занимательные задачи
Задумайте число (до 10);
Умножьте его на себя;
Прибавьте к результату задуманное число;
К полученной сумме прибавьте 1;
К полученному числу прибавьте задуманное число.
Скажите мне число, которое у вас получилось и я отгадаю, какое число вы задумали.
Решение: x² + x + 1 + x = x² + 2x + 1 = (x + 1)²
Например, 5·5 + 5 + 1 + 5 = 36,
x = √36 – 1 = 6 – 1 = 5.
Работа с учебником. Решение задачи № 900.
Самостоятельная работа. (Работа по карточкам).
I вариант II вариант
1.Преобразуйте в многочлен:
а) (у-4)2 а) (3а+4)2
б) (7х+а)2 б) (2х-в)2
в) (5с-1)(5с+1) в) (с+3)(с-3)
г) (3а+2в)(3а-2в) г) (5у-2х)(5у+2х)
2. Упростите выражение.
(а-9)2 - (81+2а) (с+в)(с-в) - (5с2-в2)
3. Разложите на множители.
а) х2-49 а) 25у2-а2
б) с2+4ас+а2 б)25х2-10ху+у2
Итоги урока.
Домашнее задание .
Оценки за урок.
Рефлексия урока: Учитель предлагает ребятам воспользоваться одной из мордашек ![]() для оценивания своей включенности в урок.
для оценивания своей включенности в урок.
б) В таблицах представлены выражения. Выберите правильный ответ.
Ответы:
| Задание | 1 | 2 | 3 |
| (с+3)2= | с2 - 6с + 9 | с2 + 2с + 9 | с2 + 6с + 9 |
| (4-2у)2= | 16 + 16у + у2 | 16 - 16у + у2 | 8 - 8у + у2 |
| (9+5х)2= | 25х2+90х+81 | 25х2+81 | 25х2-90х- 81 |
Задание. С помощью формул разложения разности квадратов на множители, найдите значение выражения.
(10+1) 2 = 121
412-312= 720
242-232 = 47
732-632 = 1360
992 = 9801
) 68 = 1
182-162
512 = 2601
Устанавливаем соответствие и получаем слово ПИФАГОР.
Пифагор










 Получите свидетельство
Получите свидетельство Вход
Вход




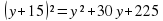
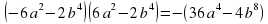
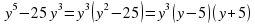
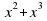 =x(16+8x+
=x(16+8x+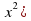
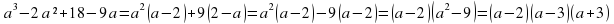


















 Конспект урока по алгебре "Формулы сокращенного умножения" (1.83 MB)
Конспект урока по алгебре "Формулы сокращенного умножения" (1.83 MB)
 0
0 512
512 91
91 Нравится
0
Нравится
0


