Открытый урок (8 класс )
Тема: «Квадратные корни. Арифметический квадратный корень».
Цели: ввести понятия квадратного корня и арифметического квадратного корня; сформировать умение извлекать квадратные корни; развивать логическое мышление, смекалку.
Оборудование: компьютер, презентация, интерактивная доска.
План урока:
Организационный момент.
Проверка домашнего задания.
Объяснение нового материала.
Формирование умений и навыков.
Самостоятельная работа (тест из ГИА)
Итоги урока.
Домашнее задание.
Ход урока:
Организационный момент.
_ Встали ровно. Здравствуйте, ребята. Садитесь. Сегодня кто дежурный в классе? Кто отсутствует? Садитесь.
Актуализация изученного знания.
_ Проверка д/з.
(Проверяем домашнее задание, к доске пойдет ______________).
Объяснение нового материала.
- Сегодня у нас не совсем обычный урок, к нам пришли гости. Давайте, улыбнемся друг другу и начнем наш урок. Послушайте стихотворение-загадку:
Он есть у дерева, цветка, он есть у уравнений,
И знак особый – радикал, с ним связан, вне сомнений
Заданий многих он итог, и с этим мы не спорим
Надеемся, что каждый смог ответить: это… (корень)
-Правильно. Сегодняшняя тема нашего урока: « Квадратный корень. Арифметический квадратный корень». Цель нашего урока: ознакомить понятиями квадратного корня и арифметического квадратного корня; развивать умение извлекать квадратные корни; воспитать аккуратность.
-Прежде, чем открыть тетради, примите правильную осанку.
-Откройте тетради, запишите число и тему урока: « Квадратный корень. Арифметический квадратный корень».
- Наш урок будет проходить под девизом: «Покоряет вершины тот, кто к ним стремится». Вершин на нашем уроке – 5, и каждый должен вложить свои усилия, чтобы покорить эти вершины.
(слайд 1)
-Устная работа. (1 вершина)
Вычислите:
а) 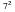 ; б)
; б) 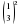 ; в)
; в) 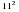 ; г)
; г) 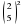 ;
;
д) 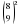 ; е)
; е) 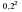 ; ж)
; ж) 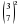 ; з)
; з) 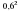 .
.
(слайд 2)
Введение понятия квадратного корня.
Рассмотрим задачу о нахождении стороны квадрата по его площади.
Пусть площадь квадрата равна 64 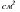 . Чему равна длина стороны этого квадрата?
. Чему равна длина стороны этого квадрата?
Обозначим длину стороны квадрата (в сантиметрах) буквой х. Тогда площадь квадрата будет 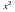 см². По условию площадь равна 64 см², значит х²=64.
см². По условию площадь равна 64 см², значит х²=64.
Корнями уравнения х²=64 являются числа: 8 и — 8. Действительно, 8²=64 и (-8)²=64. Так как длина не может выражаться отрицательным числом, то условию задачи удовлетворяет только один из корней — число 8. Итак, длина стороны квадрата равна 8 см.
Корни уравнения х²=64, т.е. Числа, квадраты которых равны 64, называют квадратными корнями из числа 64.
(слайд 3)
Задание. Вместо пустых клеточек поставьте числа так, чтобы равенства были верными:
Определение. Квадратным корнем из числа а называют число, квадрат которого равен а.
Задание: выяснить, является ли число n квадратным корнем из числа m, если:
а) n=5, m=25; в) n=0,3, m=0,9;
б) n= - 7, m=49; г) n=6, m= - 36.
(слайд 4)
Введение понятия арифметического квадратного корня.
Число 8 — неотрицательный корень уравнения х²=64 — называют арифметическим квадратным корнем из 64. Иначе говоря, арифметический квадратный корень из 64 — это неотрицательное число, квадрат которого равен 64.
Определение. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.Знак √ называют знаком арифметического квадратного корня и читают так: квадратный корень из а
Задание: определить, является ли число n арифметическим квадратным корнем из числа m, если:
а) n=8, m=64; в) n=0,2, m=0,4;
б) n= - 3, m=9; г) n=0,4, m=0,16.
(слайд 5)
Физкультминутка. Гимнастика для глаз: быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5 (повторить 2–3 раза).
Историческая справка. (2 вершина)
- Всегда интересно знать имя ученого-математика, который ввел новое понятие, либо доказал теорему, либо придумал новый математический символ. Выполнив задания, выясним имя и фамилию великого математика, который в 1637 г первым ввел знак корня.(работа парами)
| 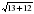 =5 =5 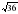 * * 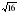 =24 =24 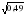 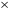 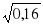 = 0,28 = 0,28 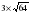 = 24 = 24 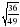 = = 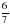 
| 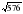 =24 =24 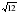 * *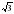 =6 =6 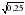 = 0,5 = 0,5
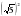 = 5 = 5
 = 3 = 3
|
Найдите значение выражения (открыли тетради, пишем только ответы)
Закончили? Поставьте буквы около того примера, ответ которой соответствует этой букве
| 
| 24 | 3 | 6 | 5 | 0,5 | 0,28 |
| д | е | т | к | р | а | н |
А теперь несколько сведений об этом математике.
Обратим внимание на совпадение в терминах — квадратный корень и корень уравнения. Это совпадение неслучайно. Уравнения вида х²=а исторически были первыми сложными уравнениями, и их решения были названы корнями по метафоре, что из стороны квадрата, как из корня, вырастает сам квадрат. В дальнейшем термин «корень» стал употребляться и для произвольных уравнений.
Название «радикал» тоже связано с термином «корень»: по-латыне корень — radix (он же редис — корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа √ связывают с написанием латинской буквы r .
Рене Декарт (1596-1650) французский дворянин, в 1629 г. переселился в Голландию. Математик, философ, мыслитель. Ввел обозначение арифметического квадратного корня .
(слайд 6)
Основное свойство арифметического квадратного корня.
Вычислите значения следующих выражений:
 ,
,  ,
,  .
.
Сформулируйте вывод:
 , если а≥0
, если а≥0
(слайд 7)
Формирование умений и навыков. (3 вершина)
-Работа по учебнику.
Самостоятельная работа (тест из ГИА). (4 вершина)
-Меняемся тетрадями и проверим задания. Ставим оценки на лист самооценки. Если правильно решено 5 заданий – ставим «5», на 4 задания – «4», на 3 задания – «3» (по уровням)
Ключ к тесту
Взаимопроверка
Итоги урока.
Что называется квадратным корнем из числа а?
Что такое арифметический квадратный корень из числа а?
Имеет ли смысл запись  ? Почему?
? Почему?
(слайд 9)
Мы смотрим телевизор часами, целый день сидим за компьютером без перерывов, разговариваем по сотовому телефону без остановки, а потом не можем понять, почему же у нас так сильно болит голова и мы так устали, что ничего не видим.
ПАМЯТКА: Помни! На компьютере рекомендуется работать не более  минут, а потом необходима зарядка для глаз, по сотовым телефонам нужно разговаривать не более
минут, а потом необходима зарядка для глаз, по сотовым телефонам нужно разговаривать не более  секунд, смотреть телевизор не более
секунд, смотреть телевизор не более  часов.
часов.
Ребята, думаю, мы справились с поставленной нами задачей.
Оценивание. А сейчас мы вам предлагаем заполнить листок самоконтроля, где вы должны будете оценить свою работу на уроке.
|
| «5» | «4» | «3» |
| 1. Задача на внимание |
|
|
|
| 2.Устный опрос |
|
|
|
| 3.Тест |
|
|
|
| 4.Практическая работа |
|
|
|
| Итог: (оцените свою деятельность на уроке) |
|
|
|
7. Домашнее задание:
(слайд 10)

 Получите свидетельство
Получите свидетельство Вход
Вход



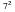 ; б)
; б) 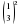 ; в)
; в) 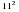 ; г)
; г) 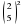 ;
; 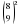 ; е)
; е) 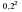 ; ж)
; ж) 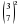 ; з)
; з) 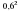 .
.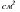 . Чему равна длина стороны этого квадрата?
. Чему равна длина стороны этого квадрата?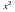 см². По условию площадь равна 64 см², значит х²=64.
см². По условию площадь равна 64 см², значит х²=64.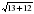 =5
=5 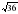 *
* 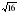 =24
=24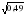
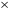
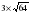 = 24
= 24 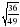 =
= 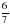

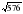 =24
=24 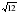 *
*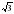 =6
=6 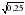 = 0,5
= 0,5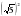 = 5
= 5








 Урок математики "Квадратные корни. Арифметический квадратный корень" (69.01 КB)
Урок математики "Квадратные корни. Арифметический квадратный корень" (69.01 КB)
 0
0 2166
2166 244
244 Нравится
0
Нравится
0


