Открытый урок по теме:
«Квадратные корни. Арифметический квадратный корень»
Учитель: Курылёва Наталья Владиславовна
Тип учебного занятия: учебное занятие по изучению и первичному закреплению новых знаний и способов деятельности.
Цель учебного занятия:
Образовательные
-дать понятие о квадратном корне из числа;
-усвоить понятие арифметического квадратного корня;
-научиться вычислять значения арифметического квадратного корня;
-сформировать умение применять их для преобразования выражений, содержащих квадратные корни;
Воспитательные:
- воспитывать внимательность, аккуратность, настойчивость
-содействовать воспитанию адекватной самооценки
Развивающие:
- развитие памяти
- развитие логического мышления
- аргументированной математической речи
Формы и методы работы:
- фронтальный (устный счет)
- индивидуальная работа с дифференциацией (карточки)
- эвристический
Оборудование: доска, мел, карточки, таблицы.
Девиз урока: Дорогу осилит идущий, а математику – мыслящий.
Логика учебного занятия:
Мотивация.
Актуализация субъективного опыта.
Восприятие и осмысление учащимися нового материала.
Первичная проверка понимания.
Первичное закрепление.
Анализ.
Рефлексия.
Ход урока.
I. Организационный момент.
Здравтвуйте!Сегодня наш урок будет посвящен изучению новой темы: «Квадратные корни. Арифметический квадратный корень»
II. Актуализация знаний.
1) Что называется степенью с натуральным показателем?
2) Основанием степени?
3) Показателем степени?
а*a*a=?
х*x*a*a=?
(x-a)*(x-a)=?
Вычислите:
(-2)2; 32; 0,72; 20; (-1)2х; (-1)2х+1
Что значит вычесть из числа a число b? (Это значит – найти такое число х=а- b, что х+b=а)
Что значит число a разделить на число b? (Это значит – найти такое число х=а : b, что х*b=а)
1. Сколько арифметических действий вы знаете?
(Сложение, вычитание, умножение, деление, возведение в степень - 5 действий.)
2. Назовите обратные им действия.
(Сложение , вычитание, умножение и деление имеют по одному обратному действию. У сложения обратное действие вычитание, у вычитания – сложение, у умножения – деление, у деления – умножение.
Пятое действие – возведение в степень имеет два обратных действия:
а) нахождение основания ; б) нахождение показателя
Определение. Нахождение основания называется извлечением корня.
Второе действие - логарифмирование. Его будем изучать в 11 классе.
Займемся 1-м действием. Так, наряду с задачей вычисления площади квадрата, сторона которого известна, с давних времен встречалась обратная задача:
Какую длину должна иметь сторона квадрата, чтобы его площадь равнялась S?
Такую задачу умели решать еще 4 тыс. лет назад вавилонские ученые
III. Изучение нового материала
Цель:
Усвоить понятие арифметического квадратного корня.
Решим задачу:
Площадь квадратного листа равна 49 м2. Чему равна длина стороны квадрата?
Решение: Пусть сторона листа – х м. Площадь S=x2 м2. Так как 72=49 и (–7)2=49, т.е. числа 7 и –7 являются корнями уравнения х2 = 49. Эти числа называются квадратными корнями.
Какой ответ в задаче? Ответ: 7 м.
Определение: Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
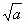 =b, b
=b, b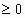 , b2=a
, b2=a
При a не имеет смысла.
При каких значениях а выражение 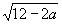 имеет смысл?
имеет смысл?
( при а 12 , т.к. 12 – а 0)
При любом а, при котором выражение 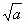 имеет смысл, верно равенство
имеет смысл, верно равенство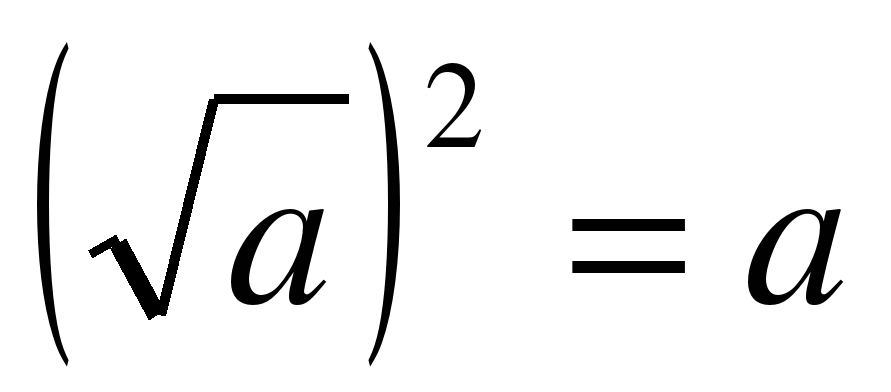
Арифметический квадратный корень обозначается значком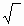 - радикал, корень.
- радикал, корень.
О ЗНАКЕ КОРНЯ. Начиная с 13 века в эпоху Возрождения итальянские и другие европейские математики обозначали корень латинским словом Radix (корень) или сокращенно R( отсюда произошел термин « радикал», которым принято называть знак корня).
Некоторые немецкие ученые в 15 веке для обозначения квадратного корня пользовались точкой, перешедших в скорописи в ромбик, а затем в черточки, вероятно, возник знак корня V (без верхней черточки). Так V4 означает 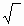 4
4
Этот знак V встречается впервые в немецкой алгебре «Быстрый и красивый счет при помощи искусных правил алгебры. Знаком корня пользовались в 16 веке с цифрой 2 в круге. В 1626 году нидерландский математик А.Ширар ввел близкое к современному обозначение корня V. Если над этим знаком стояла цифра 2, то это означало корень квадратный.
Это обозначение стало вытеснять знак R. Однако долгое время писали V а+в с горизонтальной чертой над суммой. Лишь в 1637 году Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня 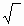 . Этот знак вошел во всеобщее употребление лишь в начале 18 века в книге « Руководство алгебры» французского математика М. Роля ( 1652 – 1719).
. Этот знак вошел во всеобщее употребление лишь в начале 18 века в книге « Руководство алгебры» французского математика М. Роля ( 1652 – 1719).
Знак корня был введен практической необходимостью, зная площадь людям в 16 веке нужно было вычислять сторону квадрата. Для этого был введен корень квадратный.
Примеры:
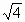 =2, т.к. 2
=2, т.к. 2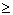 0, 22=4
0, 22=4
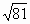 =9, т.к. 9
=9, т.к. 9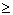 0, 92=81
0, 92=81
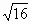
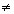 -4, т.к. –4
-4, т.к. –4
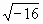
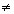 4, т.к. 42
4, т.к. 42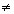 -16
-16
Из истории. Ещё 4000 лет назад вавилонские ученые составили наряду с таблицами умножения и таблицами обратных величин ( при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа.
Обратить внимание на таблицу квадратов на втором форзаце учебника
Используя, таблицу решить № 306 (а, б)
IV. Закрепление нового материала
Цель:
Закрепить определения квадратного корня. Научиться вычислять значения арифметического квадратного корня.
Выполнить:
298 ( устно)
Докажите, что:
а) число 5 есть арифметический квадратный корень из 25 (т.к. 5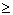 0, 52=25)
0, 52=25)
б) число 0.3 есть арифметический квадратный корень из 0.09 (т.к. 0.3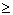 0, 0.32=0.09)
0, 0.32=0.09)
в) число –7 не является арифметическим квадратным корнем из 49 ( т.к. –7
г) число 0,6 не является арифметическим квадратным корнем из 3,6. (0,6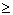 0, но о,62
0, но о,62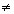 3,6)
3,6)
№ 300,
№ 304,
№ 306,
V. Обобщение:
Цель:
Привести в систему полученные знания, научиться рассуждать при решении задач, делать самостоятельные выводы.
С этой целью выполните самостоятельно следующие задания ( Приложение 1):
| 1 вариант 1. Найдите значение корня а) 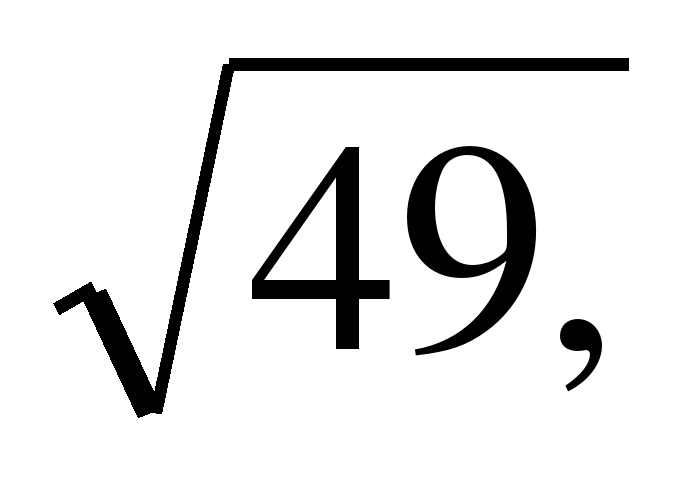 б) б) 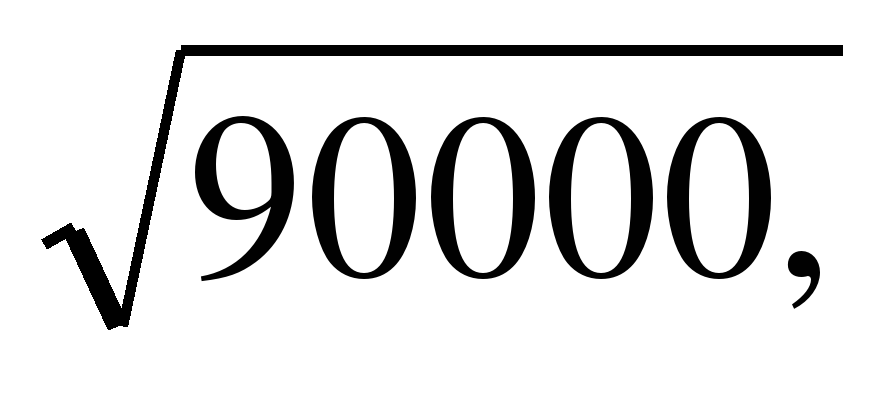 в) в) 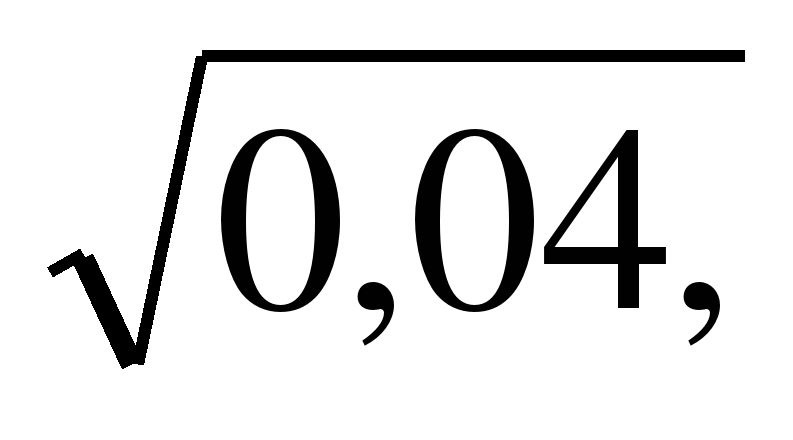 г) г) 2. Вычислите а) б) 0,1+ 3. При каких значениях с имеет смысл выражение а) б) в) г)
| 2 вариант 1. Найдите значение корня а) б) в) г) . 2. Вычислите а) б) 3. При каких значениях b имеет смысл выражение а) б) в) г)
|
VI. Итог урока. Что вы узнали нового сегодня на уроке?
Сформулировали определение квадратного корня, выяснили, что называется арифметическим квадратным корнем, узнали, как изменялся исторически знак радикала, научились вычислять арифметический квадратный корень.
VII. Домашнее задание: п. 12 стр. 70 – 71, № 299, 301, 305, 309.
К математике способность проявляйте,
Не ленитесь, ежедневно развивайтесь.
Умножайте, делите, вычитайте,
С математикой дружить не забывайте.
- Урок окончен. Спасибо. До свидания.
Приложение 1.
| 1 вариант 1. Найдите значение корня а) 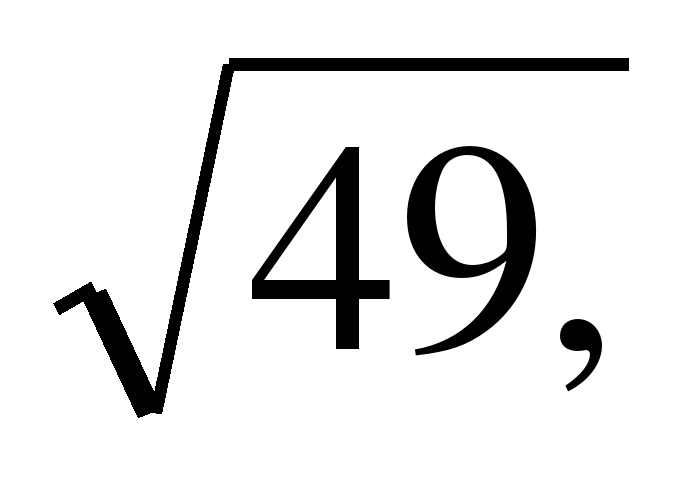 б) б) 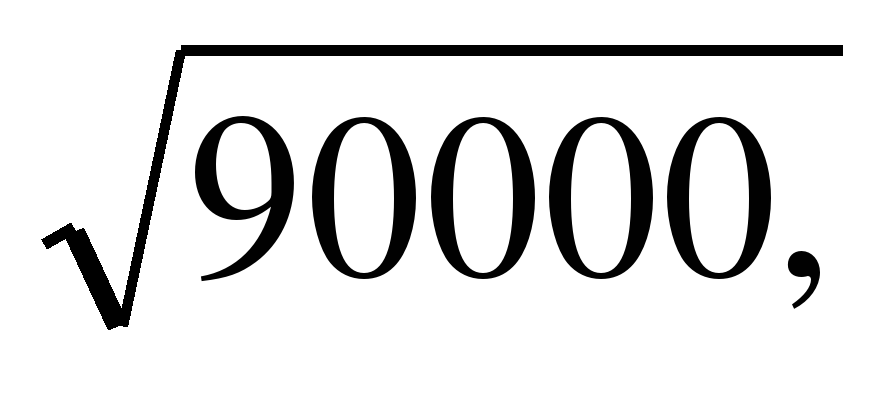 в) в) 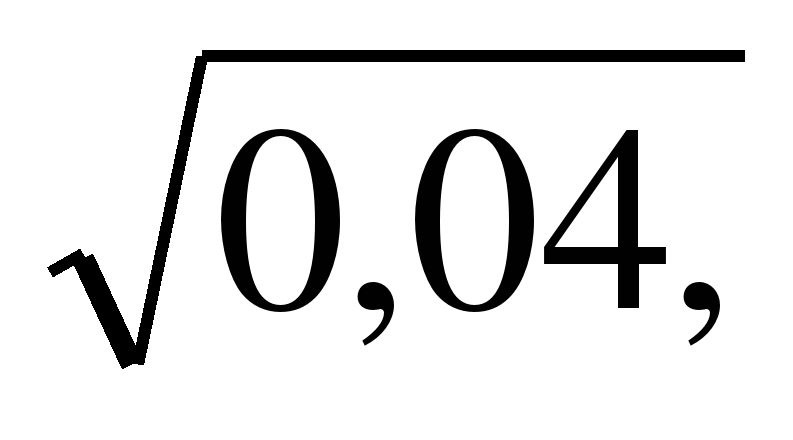 г) г) 2. Вычислите а) б) 0,1+ 3. При каких значениях с имеет смысл выражение а) б) в) г)
| 2 вариант 1. Найдите значение корня а) б) в) г) . 2. Вычислите а) б) 3. При каких значениях b имеет смысл выражение а) б) в) г)
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок математики «Квадратные корни. Арифметический квадратный корень» (0.11 MB)
Урок математики «Квадратные корни. Арифметический квадратный корень» (0.11 MB)
 0
0 2344
2344 403
403 Нравится
0
Нравится
0


