Задачи урока:
Образовательные - ввести понятия доли и обыкновенной дроби, научить применять их при решении задач, создать основу для дальнейшего изучения обыкновенных дробей.
Развивающие - продолжить формирование информационной и проблемной компетенций, развитие логического мышления, памяти, внимания.
Воспитательные – продолжить формирование коммуникативной и кооперативной компетенций
Необходимое оборудование и материалы: конструктор из магнитных геометрических фигур, цветные карандаши, портреты Фибоначчи и Максима Плануда, картонные прямоугольники различных цветов.
Ход урока:
Организационный момент (2 мин. )
Здравствуйте, ребята. Садитесь.
Ребята, у нас есть поговорка «Попал в тупик». В чём смысл этой поговорки?
(заслушиваются ответы детей) Эта поговорка означает, что человек попал в трудное положение.
Почему мы начали урок с этой поговорки, вы поймёте по ходу урока.
Создание проблемной ситуации, обозначение темы урока (15 мин. )
Разделите все примеры на группы по различным признакам. Какие из этих примеров вы бы объединили в одну группу и почему?
16 : 2; 16 : 5; 2 : 3; 9 : 3; 8 : 4; 3 : 5; 15 : 5.
Дениска, герой рассказов Драгунского, задал однажды приятелю Мишке задачу: как разделить 2 яблока на 3? И когда Мишка, наконец, сдался, торжествующе объявил ответ: «Сварить компот!» Мишка с Денисом ещё не проходили дробей и твердо знали, что 2 на 3 не делится.
Попробуйте вы справиться с этой задачей. Как бы вы разделили 2 яблока на троих. Заслушиваются варианты детей, выбираются самые оптимальные.
1
3 доля (часть)
2
3 обыкновенная дробь
2 – числитель (сколько таких частей взято)
3 – знаменатель (На сколько частей делят)
Каждый может за версту
Видеть дробную черту.
Над чертой – числитель, знайте,
Под чертою знаменатель.
Дробь такую непременно
Надо звать обыкновенной.
А что по вашему означает слово «дробь» (дробить, ломать, разбить)
Доклад ученика о том, как появились дроби.
Вернёмся к поговорке, с которой мы начали урок «Попал в тупик»
У немцев аналогичная поговорка гласит «Попасть в дроби». Эта поговорка напоминает о тех временах, когда дроби считали самым трудным, самым запутанным разделом математике (так как общих приёмов действий с дробями не было) В наши дни дроби начинают изучать уже в младших классах
Как же мы сформулируем тему нашего сегодняшнего урока?
(Доли. Обыкновенные дроби)
Закрепление изученного материала (15 мин. )
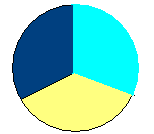
Начертите 3 квадрата со стороной 2 см. Разделите их на 4 равные части (доли) различными способами. Закрасьте:
1
4 первого квадрата
2
4 второго квадрата
3
4 третьего квадрата
Учитель собирает из пластин конструктора разные фигуры и просит назвать и написать соответствующие дроби (например, какая часть фигуры закрашена в жёлтый цвет) Затем фигуры собирают учащиеся по очереди. Учитель просит показать дроби 1/5, 2/6, 4/7, 4/8, 1/2 (различные способы)
Ученики по очереди собирают фигуры на доске, а все остальные из картонных прямоугольников собирают фигуры на партах.
А теперь давайте посчитаем, какую часть присутствующих в классе составляют ученицы, ученики, гости.
Работа у доски с полным объяснением решения:
3/10ч =… мин. 3/5т =… кг.
16/100м =… дм … см 2/5 дм =… см
3/4сут =…ч 7/10ц =…кг
Учитель читает задачи, дети записывают только ответы:
- Сколько минут в пятой части часа?
- Сколько дециметров в половине метра
- Сколько часов в трети суток?
- Сколько секунд в четвёртой части минуты?
- Прошла пятая часть века и ещё 2 года. Сколько это лет?
- Всего в новой книге про Таню Гроттер 450 страниц. За 1 день Миша прочитал одну десятую часть книги. Сколько он прочитает за 3 дня?
Задача № 6 с недостатком информации, как можно изменить условие задачи, чтобы её можно было решить? Заслушиваются ответы детей, решаем одну из предложенных задач.
Самостоятельная работа (8 мин. )
Работа по карточке 1. Это самостоятельная работа обучающего характера с последующей выборочной проверкой. Аналогичные фигуры вывешиваются на доску.
Рефлексия (5 мин. )
Итог урока: Что нового узнали на уроке, как (где) применяли полученные знания (умения).
Выставление оценок за урок.
Нам доли всякие нужны
Нам дроби разные важны.
Усердно изучайте их
И к вам придёт удача
Коль дроби будете вы знать
И точный смысл их понимать
То станет лёгкой
Даже трудная задача.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок математики "Доли. Обыкновенные дроби" (52.98 КB)
Урок математики "Доли. Обыкновенные дроби" (52.98 КB)
 1
1 965
965 116
116 Нравится
0
Нравится
0