Цель: Познакомить с основными логическими операциями: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
Задачи:
Сформировать у учащихся понятие “логическая операция»;
Способствовать формированию логического мышления, интереса к изучаемому материалу.
Ожидаемые результаты:
Учащиеся должны знать:
логические операции: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность;
таблицы истинности логических операций;
обозначение логических операций;
приоритет логических операций.
Учащиеся должны уметь:
определить порядок действий при вычислении значения логического выражения;
конструировать простые и сложные высказывания.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
III. Изложение нового материала.
Основным понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что - либо о чем - либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».
Логическая операция — способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Рассмотрим три базовых логических операций — инверсию, конъюнкцию, дизъюнкцию и дополнительные — импликацию и эквивалентность.
Отрицание (инверсия)
Отрицанием высказывания х называется новое высказывание, которое является истинным, если высказывание х ложно, и ложным, если высказывание х истинно.
Отрицание высказывания х читается «не х» или «неверно, что х».
Логические значения высказывания можно описать с помощью таблицы.
Таблицы такого вида принято называть таблицами истинности.
Конъюнкция.
Конъюнкцией (логическим умножением) двух высказываний х и у называется новое высказывание, которое считается истинным, если оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний х и у обозначается символом х&у (, ху ) , читается «х и у».
Логические значения конъюнкции описываются следующей таблицей истинности:
Дизъюнкция
Дизъюнкцией (логическим сложением) двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны.
Дизъюнкция высказываний х, у обозначается символом «x V у» , читается «х или у». Высказывания х, у называются членами дизъюнкции.
Логические значения дизъюнкции описываются следующей таблицей истинности:
Импликация.
Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, если х истинно, а у - ложно, и истинным во всех остальных случаях.
Импликация высказываний х, у, читается«если х, то у» или «из х следует у».
Логические значения операции импликации описываются следующей таблицей истинности:
Эквивалентность.
Эквивалентностью двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквивалентность высказываний х, у читается«для того, чтобы х, необходимо и достаточно, чтобы у» или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквивалентности.
Логические значения операции эквивалентности описываются следующей таблицей истинности:
Упражнение 1. Даны два простых высказывания:
А= “Аист – птица”;
В=“Щука — речная рыба”.
Составьте из них все возможные составные (сложные) высказывания и определите их истинность.
При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
инверсия
конъюнкция
дизъюнкция
импликация и эквивалентность
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



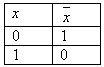 Таблицы такого вида принято называть таблицами истинности. Конъюнкция. Конъюнкцией (логическим умножением) двух высказываний х и у называется новое высказывание, которое считается истинным, если оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно. Конъюнкция высказываний х и у обозначается символом х&у (
Таблицы такого вида принято называть таблицами истинности. Конъюнкция. Конъюнкцией (логическим умножением) двух высказываний х и у называется новое высказывание, которое считается истинным, если оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно. Конъюнкция высказываний х и у обозначается символом х&у ( 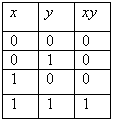 Дизъюнкция Дизъюнкцией (логическим сложением) двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны. Дизъюнкция высказываний х, у обозначается символом «x V у» , читается «х или у» . Высказывания х, у называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:
Дизъюнкция Дизъюнкцией (логическим сложением) двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны. Дизъюнкция высказываний х, у обозначается символом «x V у» , читается «х или у» . Высказывания х, у называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:  Импликация. Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, если х истинно, а у - ложно, и истинным во всех остальных случаях. Импликация высказываний х, у обозначается символом
Импликация. Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, если х истинно, а у - ложно, и истинным во всех остальных случаях. Импликация высказываний х, у обозначается символом 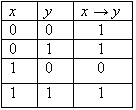 Эквивалентность. Эквивалентностью двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквивалентность высказываний х, у обозначается символом
Эквивалентность. Эквивалентностью двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквивалентность высказываний х, у обозначается символом 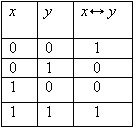









 Урок информатики "Логические операции над высказываниями" (0.1 MB)
Урок информатики "Логические операции над высказываниями" (0.1 MB)
 0
0 3722
3722 401
401 Нравится
0
Нравится
0


