Получите свидетельство
Вход
Школа-гимназия
имени С.М. Кирова
с. ТЕПЛОКЛЮЧЕНКА
2019-2020 уч.год
Урок геометрии
в 9 классе
« Площадь круга и его частей".
Учитель математики
Князева Ольга Владимировна
Игра – разминка.
Вы отвечаете на мои вопросы, записывая первую букву каждого ответа.
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. Как называется эта теорема ?
- к осинусов
Как называется любой отрезок, соединяющий точку окружности с ее центром?
- р адиус
Как называется геометрическая фигура, образованная двумя лучами, исходящими из одной точки?
Они бывают развернутыми, тупыми, прямыми, острыми, а у окружности он называется центральным
- у гол
Единица измерения угла
- г радус
Круг
Круг
- Что называется
круговым сектором?
Круг
- Что называется
круговым сегментом?
Длина окружности
С= 2πR.
Теорема
Площадь S круга радиусом R равна
S= 1/2 СR= πR 2
Площадь кругового сектора
Так как площадь всего круга равна S=πR 2 , то площадь кругового сектора, ограниченного дугой в 1º равна πR 2 /360 . Поэтому площадь сектора, ограниченного дугой с градусной мерой α выражается формулой
Площадь кругового сектора
Рассмотрим круговой сектор, изображённый на рисунке, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего
центрального угла .
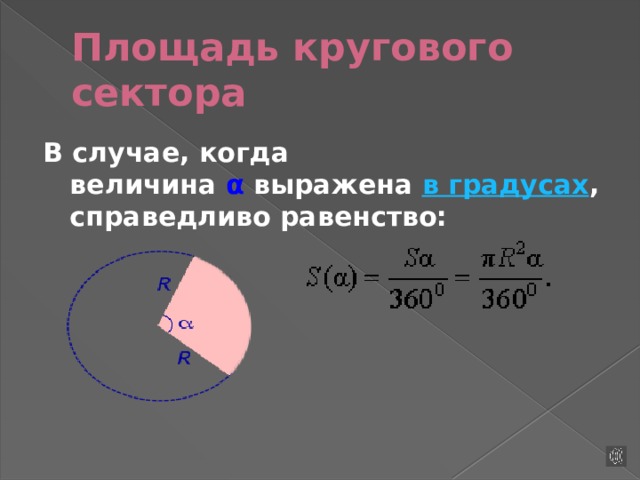
Площадь кругового сектора
В случае, когда величина α выражена в градусах , справедливо равенство:
Площадь кругового сектора
В случае, когда величина α выражена в радианах , справедливо равенство:
Площадь кругового сегмента.
Рассмотрим круговой сегмент, изображённый на рисунке, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла .
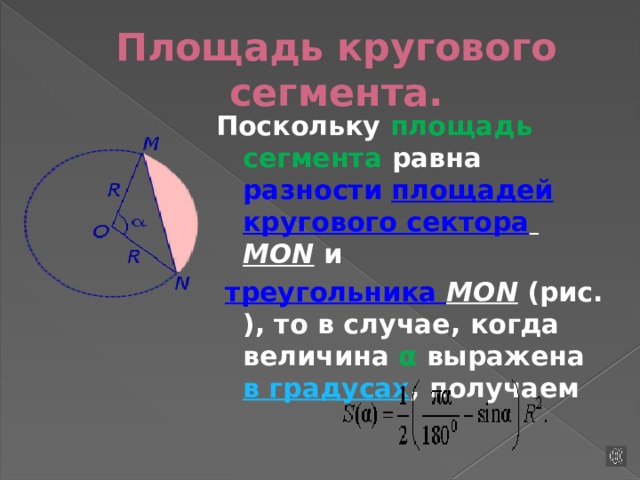
Площадь кругового сегмента.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и
треугольника MON (рис.), то в случае, когда величина α выражена в градусах , получаем
Площадь кругового сегмента.
В случае, когда величина α выражена в в радианах , получаем
180º. S сег = S сек ± S Δ " width="640"
Площадь кругового сегмента.
- Чтобы вычислить площадь сегмента нужно из площади соответствующего сектора вычесть площадь треугольника , если α , или прибавить ее, если α180º. S сег = S сек ± S Δ
Решение задач.
1)Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 см и 12 см.(Рис.1)
Дано: окр (О;r), r= 12 см
окр (O; R) R= 1 см
Найти: S кольца
Решение. Из площади большего круга вычесть площадь меньшего круга, т.к. центры совпадают.
Но для этого мы вначале должны найти площади кругов, S=πR 2
S=π12 2 =144π
S=π13 2 = 169π
r
R
рис1
Решение задач.
2)Площадь кругового сектора равна , а его центральный угол равен . Найти радиус сектора и площадь сегмента, опирающегося на центральный угол.(Рис.2)
Дано: Окр (О: R)
β=40°
S =18π см 2
Найти: R, S сегмента
О
Решение: Площадь сегмента находится по формуле
Из нее мы можем выразить радиус сектора, зная площадь сектора и градусную меру дуги сектора:
В
А
Рис.2 2
Но это не полное решение задачи. Нам еще нужно найти площадь сегмента, опирающегося на угол в 40° . Каким образом это можно осуществить?
Найдем площадь АОВ, а потом вычтем из площади сектора площадь АОВ, тем самым найдем площадь искомого сегмента.
Ответ:
Тесты с выбором ответа.
1) Чему равна дуга окружности (в градусах), стягиваемая стороной правильного треугольника? А) 60 0 ; Б) 120 0 ; В) не знаю. 2) Сколько сторон имеет правильный многоугольник, у которого сумма всех углов равна 540 0 ? А) 5; Б) 6; В) не знаю. 3) Чему равна длина окружности, если ее диаметр равен 50 см? А) 50 п см; Б)25 п см; В) не знаю. 4) Из круга, радиус которого равен 20 см, вырезан сектор. Дуга сектора равна 90 0 . Чему равна площадь оставшейся части круга? А) 100 п см 2 ; Б) 300 п см 2 ; В) не знаю.
Самопроверка
Код ответа:
- Б
- Б
- А
- А
Дома:
№ 55(1).
Дома:
Тесты: Установите, истинны или ложны высказывания: поставить знаки «+» или «-» при выборе ответа 1) Любой треугольник является правильным, если все его углы равны. 2) Около любого правильного многоугольника можно описать окружность и притом только одну.
3) Окружность, касающаяся всех сторон многоугольника, называется вписанной. 4) Если все вершины многоугольника лежат на окружности, то окружность называется описанной. 5) Многоугольник является правильным, если все его углы равны. 6) Окружность, вписанная в правильный многоугольник, касается каждой стороны многоугольника в его середине.
7) Сторона правильного треугольника, вписанного в окружность, выражается через радиус этой окружности по формуле а = R . 8) Длину окружности можно вычислить по формуле С = пD, где D - диаметр окружности. 9) Площадь круга равна произведению квадрата его радиуса на п. 10) cos 0° = 0 (Обратить внимание на задание 7). Выяснить правильность записи.
Урок геометрии в 9 классе "Площадь круга и его частей" (6.78 MB)
0
341
39
Нравится
0
