Урок алгебры в 9 классе по теме « Свойства арифметического корня n- степени»
Выполнила Корзюк Н.Н.- учитель математики МКОУ Куминская СОШ.
| Цели урока: | Ввести свойства арифметического корня n- степени. Научить применять эти свойства в упрощении выражений, содержащих корни n- степени; Развитие коммуникативных навыков и навыков самостоятельной работы; Воспитывать умения самооценки и взаимовыручки, ответственного отношения к учебе. | ||||||||
| Ход урока. | По технологии КСО. | ||||||||
| 1.Орг. момент | Мотивация. « Используйте 6 слуг. Они помогут вам везде! Зовут их : КАК И ПОЧЕМУ, КТО.,ЧТО, КОГДА И ГДЕ!» - На что нацеливают вас эти слова? ( Слушаем ответы учащихся) | ||||||||
| 2. Актуализация знаний Учащихся | На доске запись: - Прочитайте запись. Чем является а, чем является n? - Повторим свойства квадратных корней, изученных в 8 классе.
| ||||||||
| 4.Изучение нового материала
-Формулировка темы урока. - Ставим задачи на самостоятельную работу. | Создание проблемной ситуации. Задание на доске. Упростить выражение: - Как это сделать? - Не знаем! -На сегодняшний момент наших знаний недостаточно! -Какую тему урока выберем? Записать на доске: « СВОЙСТВА арифметического корня n- степени» - Мы повторили свойства квадратных корней. Аналогичными свойствами обладает арифметический корень n- степени. -Сейчас вам предстоит самостоятельно изучить эти свойства и научиться их применять. -Работаем в парах сменного состава ( Изучаем карточку №1,2,3) и в парах постоянного состава( Взаимообмен карточками) . -Работаем по алгоритму. -Проверяем себя по карточкам самоконтроля ( С.К.) - Проводим самооценку своей работы. | ||||||||
| 4.Первичный контроль знаний. | Контролирующая карточка по вариантам. КОД: Б.А.А.Б.А.Б. | ||||||||
| 5.Итог урока | 1) Выставите себе оценку за урок ( среднее арифметическое) 2) С чем мы познакомились на уроке? ( Возврат к банку знаний) 3)Возврат к проблемной ситуации: Вы разобрались, как упростить выражение | ||||||||
| 6.Рефлексия. | Выберите для себя утвердительный ответ на один из вопросов: Я все понял на уроке! 2) Я старался, но нужна доработка материала. 3) Я ничего не понял. | ||||||||
| 7. Д/З ( Дифференцированно) | 1) База: № 544(а,в), № 546, 3 559 ( б.г.е) 2) продвинутый уровень + № 550(а,б) 3) * + № 553(а,б) | ||||||||
Приложение. ( Раздаточный материал для обучающихся).
Карточка № 1.
Свойства степени с целым показателем.
| Правило произведения степеней | Если а –любое число, а n и m любые целые числа, то
Читается так: При умножении степеней с одинаковым основанием основания остаются прежними, а показатели степеней складываются. |
| Пример. | Упростим выражение: Найти значение выражения: |
| Закрепи материал. | Учебник, стр. 47-48, № 157(а б), № 158(б), № 161 ( а, б, в) |
Карточка №2
Свойства степени с целым показателем.
| Частное степеней | Если а –любое число, не равное 0, а n и m любые целые числа,
Читается так: При делении степеней с одинаковым основанием основания остаются прежними, а из показателя степени делимого вычитается показатель степени делителя. |
| Пример. | Упростим выражение: Найти значение выражения: |
| Закрепи материал. | Учебник, стр. 47-48, № 157(в, г), № 158(а), № 161 ( д, г) |
Карточка №3
Свойства степени с целым показателем
| Возведение степени в степень | Если а –любое число, а n и m любые целые числа, Читается так: При возведении степени в степень основание остаётся прежними, а показателя степеней перемножаются.
|
| Пример. | Упростим выражение: Найти значение выражения:
|
| Закрепи материал. | Учебник, стр. 48-49, № 157(д, е), № 158(в, г), № 160 ( д, е) |
Контролирующая карточка.
вариант.
1)Упростите выражение:
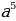 ∙
∙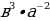 ∙
∙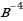 А:
А:  ∙
∙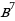 Б:
Б: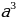 ∙
∙ В:
В: 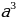 ∙
∙
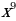 :
: 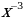 А:
А:  Б:
Б: В:
В: 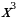
 А:
А: 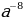 Б:
Б: В:
В: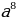
2) Вычислите:
1)  ∙
∙ А: 81 Б: 9 В:
А: 81 Б: 9 В: 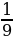
2)  :
: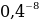 А: 0,16 Б: 0,016 В: 0, 0016
А: 0,16 Б: 0,016 В: 0, 0016
3) 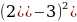 А: 64 Б:
А: 64 Б: 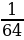 В:
В: 
Контролирующая карточка.
вариант.
1)Упростите выражение:
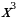 ∙
∙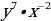 ∙
∙ А:
А: 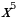 ∙
∙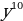 Б:
Б: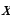 ∙
∙ В: х∙
В: х∙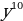
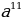 :
: 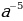 А:
А: 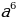 Б:
Б: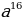 В:
В: 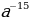
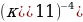 А:
А: 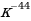 Б:
Б: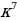 В:
В: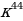
2) Вычислите:
1) 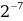 ∙
∙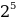 А: 4 Б: -
А: 4 Б: -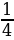 В:
В: 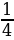
2)  :
: А: 16 Б: -16 В:
А: 16 Б: -16 В: 
3) 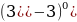 А:
А:  Б:1 В: -27
Б:1 В: -27

 Получите свидетельство
Получите свидетельство Вход
Вход



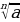 .
.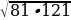 ;
; ;
;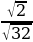 ;
;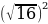 .
.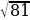
 =9 ∙11=99;
=9 ∙11=99;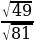 =
= 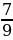 ;
;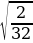 =
=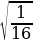 =
=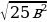 ;
; ;
;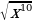 .
.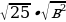 =5∙│в│;
=5∙│в│;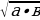 =
= ∙
∙ , где а≥ 0, в≥0 ;
, где а≥ 0, в≥0 ;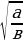 =
=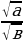 , где а≥ 0, в0 ;
, где а≥ 0, в0 ; =│а│.
=│а│. 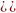 , где а0, в0 ;
, где а0, в0 ; 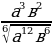 =
= 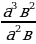 =ав )
=ав )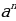 ∙
∙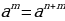 .
.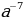 ∙
∙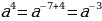 ;
;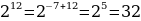 ;
;
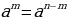 .
.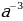 :
: 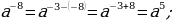
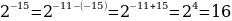
 .
.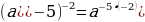 =
=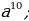
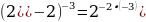 =
= = 64
= 64








 Урок алгебры в 9 классе по теме «Свойства арифметического корня n- степени» (31.1 KB)
Урок алгебры в 9 классе по теме «Свойства арифметического корня n- степени» (31.1 KB)
 0
0 110
110 0
0 Нравится
0
Нравится
0


