Урок "5 графических способов решения квадратных уравнений" 8 класс.

Тема: 5 графических способов решения квадратных уравнений.

Цель урока: применение навыков построения графиков функций при решении квадратных уравнений

Ход урока.

1. Актуализация знаний.

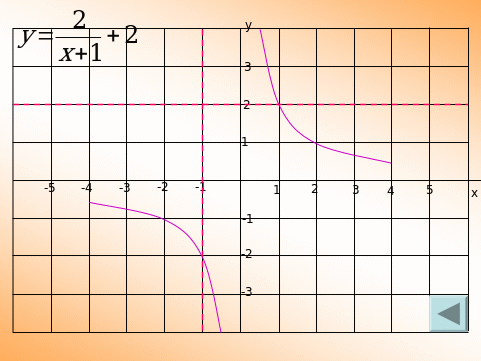
• Движение графиков функций на плоскости. (Слайд 4)

Прокомментировать движение графика функции.

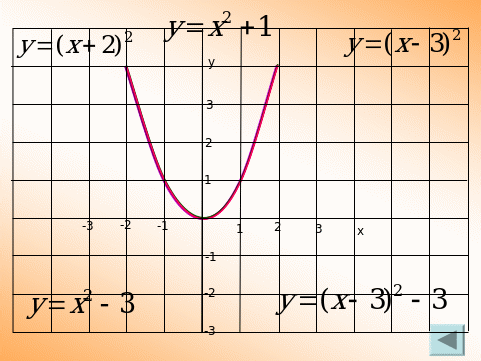
• Объяснить построение графика функции. (Слайды 5 – 8)

а) направление ветвей; б) роль k; в) движение на плоскости.

После обсуждения график преобразуется в соответствующий вид.

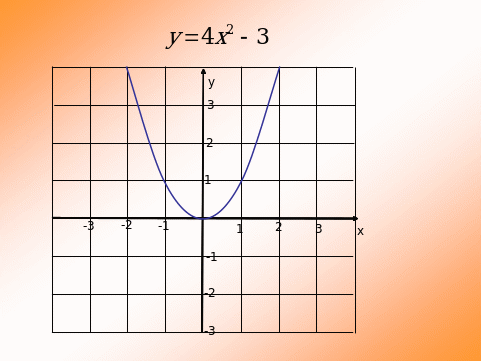
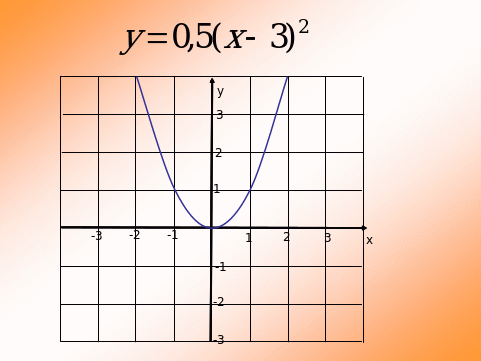
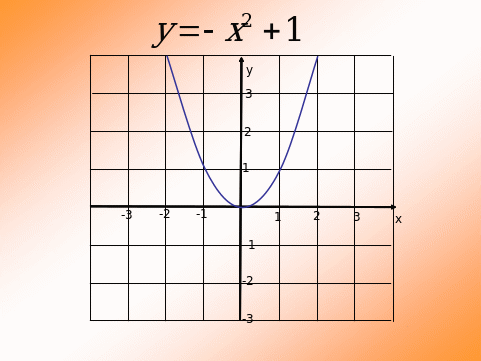
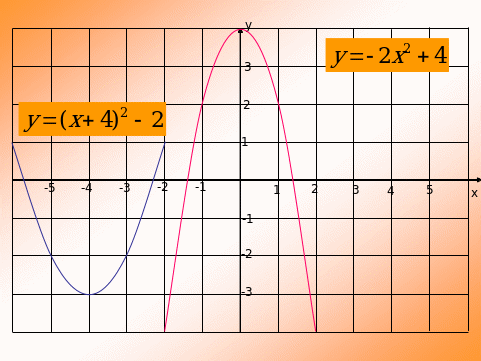
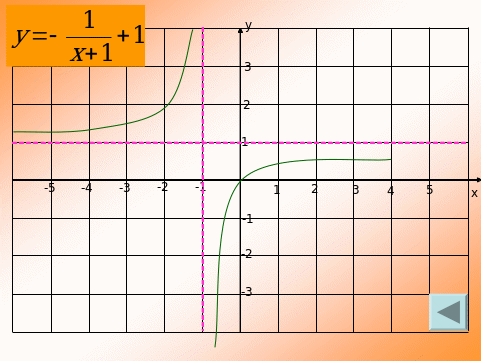
• По графику функции написать ее уравнение. (Слайды 9 – 11)

• Построить график функции у = ах² + bx + c. (Слайд 12)

Перед построением вспоминаем алгоритм построения графика:

направление ветвей;

формулы вершины параболы;

роль коэффициентов а и с.

1. Новый материал.

П ять способов решения квадратных уравнений. (Слайды 13 – 17)

Решить уравнение

I способ. Строим график функции у = х² – 2х – 3 и находим точки его

пересечения с осью абсцисс.

II способ. Преобразуем уравнение к виду х² = 2х + 3. Построим графики

функций у = х² и у = 2х + 3. Находим точки пересечения параболы и

прямой.

III способ. Преобразуем уравнение к виду х² = 2х + 3. Построим графики

функций у = х² - 3 и у = 2х. Находим точки пересечения параболы и

прямой.

IV способ. Применим способ выделения полного квадрата, получим

(х – 1)² – 4 = 0. Построим графики функций у = (х – 1) ² и у = 4.

Находим точки пересечения параболы и прямой.

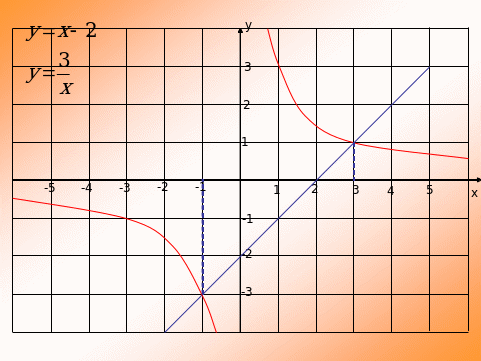
V способ. Разделим обе части уравнения на х, получим уравнение вида

, построим графики функций у = х – 2 и у = .

Находим точки пересечения гиперболы и прямой.

1. Практическое применение умений и навыков.

Выберите способ и решите уравнение

• х² – 4х + 5 = 0 ( корней нет)

• х² - х – 3 = 0

Чему равны корни уравнения на графике точно определить нельзя.

Вывод:

Графические способы красивы, но не дают гарантии решения любого квадратного уравнения !!!

Эту проблему мы решим на следующем уроке!

4. Домашнее задание: № 520, 525