Уравнение касательной к графику функции

Уравнение касательной к графику функции

Тип урока: изучение нового материала.

Методы обучения: наглядный, частично поисковый, групповой.

Цель урока.

1. Ввести понятие касательной к графику функции в точке, выяснить в чем состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.

2. Развивать логическое мышление, математическую речь.

План урока

I. Организационный момент

Проверка готовности учащихся к уроку. Сообщение темы урока и целей.

II. Актуализация знаний.

(Вспомнить с учащимися геометрическое определение касательной к графику функции. Привести примеры, показывающие, что данное утверждение не полно.)

Вспомним, что же такое касательная?

“Касательная – это прямая, имеющая с данной кривой одну общую точку”.

Обсуждение правильности данного определения. (После обсуждения, учащиеся приходят к выводу, что данное определение неверно.) Для наглядного доказательства их умозаключения приводим следующий пример.

Рассмотрим пример.

Пусть дана парабола y = x² и две прямые x = 2,y = 4x - 4, имеющая с данной параболой одну общую точку A (2;4). Проводится обсуждение, почему первая прямая не является к данной параболе касательной (Рис. 1), а вторая является (Рис.2).

рис.1 рис.2

На данном уроке, мы с вами должны выяснить, что же такое касательная к графику функции в точке, как составить уравнение касательной?

Рассмотреть основные задачи на составление уравнения касательной.

III. Определение

Пусть дана функция f, которая в некоторой точке x₀ имеет конечную производную f(x₀). Тогда прямая, проходящая через точку (x₀; f (x₀)), имеющая угловой коэффициент f’(x₀), называется касательной.

А что будет, если производная в точке x₀ не существует? Возможны два варианта:

1. Касательная к графику тоже не существует. Классический пример — функция

y = =|x| в точке (0; 0).

1. Касательная становится вертикальной. Это верно, к примеру, для функции

y = arcsin x в точке (1; ).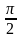

IV. Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x₀, достаточно знать значение функции и производной в этой точке.

V. Алгоритм составления уравнения касательной к графику функции y = f(x)

1. Обозначить буквой a абсциссу точки касания.
2. Найти f(x₀).
3. Найти f '(x) и f '(x₀).
4. Подставить найденные числа x₀, f(x₀), f '(x₀) в общее уравнение касательной

y = f(x₀) + f '(x₀)(x – x₀).

В первом типе задач были выделены две ключевые задачи:

• касательная проходит через точку, лежащую на кривой (задача 1);

• касательная проходит через точку, не лежащую на к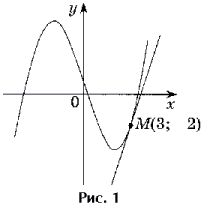 ривой (задача 2).

Задача 1. Составьте уравнение касательной к графику функции y = 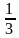x³ – 4x + 1в точке M(3; – 2).

Решение. Точка M(3; – 2) является точкой касания, так как

f(3) =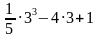

1. x₀ = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f '(x) = x² – 4, f '(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

Задача 2. Напишите уравнения всех касательных к графику функции y = – x² – 4x + 2, проходящих через точку M(– 3; 6).

Р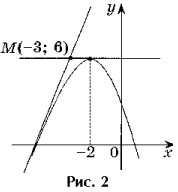 ешение. Точка M(– 3; 6) не является точкой касания, так как f(– 3) ­ ≠ 6 (рис. 2).

1. x₀ – абсцисса точки касания.
2. f(x₀) = – a² – 4a + 2.
3. f '(x) = – 2x – 4, f '(a) = – 2a – 4.
4. y = – a² – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.

Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.

6 = – x₀² – 4x₀ + 2 – 2(x₀ + 2)(– 3 – x₀),
x₀² + 6x₀ + 8 = 0 .

x₀= – 4, x₀ = – 2.

Если x₀ = – 4, то уравнение касательной имеет вид y = 4x + 18.

Если x₀ = – 2, то уравнение касательной имеет вид y = 6.

Во втором типе ключевыми задачами будут следующие:

• касательная параллельна некоторой прямой (задача 3);

• касательная проходит под некоторым углом к данной прямой (задача 4).

Задача 3. Напишите уравнения всех касательных к графику функции y = x³ – 3x² + 3, параллельных прямой y = 9x + 1.

Решение.

1. x₀ – абсцисса точки касания.

2.  f(x₀) = x₀³ – 3x₀² + 3.

3. f '(x) = 3x² – 6x, f '(x₀) = 3x₀² – 6x₀.

Н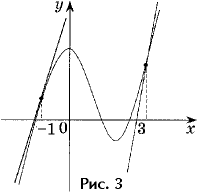 о, с другой стороны, f '(x₀) = 9 (условие параллельности). Значит, надо решить уравнение 3x₀² – 6x₀ = 9. Его корни

x₀ = – 1, x₀ = 3 (рис. 3).

4. 1) x₀ = – 1;
2) f(– 1) = – 1;
3) f '(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – уравнение касательной;

1) x₀ = 3;
2) f(3) = 3;
3) f '(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – уравнение касательной.

З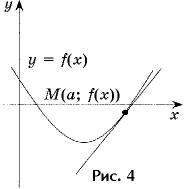 адача 4. Напишите уравнение касательной к графику функции y = 0,5x² – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. 4).

Решение. Из условия f '(a) = tg 45° найдем a:  a – 3 = 1 ^ a = 4.

1. x₀= 4 – абсцисса точки касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f '(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – уравнение касательной.

Несложно показать, что решение любой другой задачи сводится к решению одной или нескольких ключевых задач.

Рассмотрим в качестве примера следующую задачу.

Н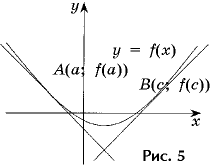 апишите уравнения касательных к параболе

y = 2x² – 5x – 2, если касательные пересекаются под прямым углом и одна из них касается параболы в точке с абсциссой 3 (рис. 5).

Решение. Поскольку дана абсцисса точки касания, то первая часть решения сводится к ключевой задаче 1.

1. x₀= 3 – абсцисса точки касания одной из сторон прямого угла.
2. f(3) = 1.
3. f '(x) = 4x – 5, f '(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой касательной.

2.Пусть a – угол наклона первой касательной. Так как касательные перпендикулярны, то 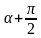– угол наклона второй касательной. Из уравнения y = 7x – 20 первой касательной имеем tg a = 7.

Найдем tg(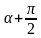 ) = - ctg = -

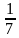
Это значит, что угловой коэффициент второй касательной равен - .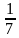

Дальнейшее решение сводится к ключевой задаче 3.

Пусть B(c; f(c)) есть точка касания второй прямой, тогда

f´(c) = 4c – 5c = - 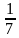= c =

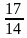
1. c = 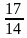– абсцисса второй точки касания.
   2. f (  = -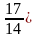
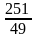
   3.  f ´ (  = -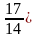
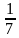
   4. y =  -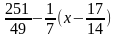

y = 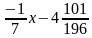– уравнение второй касательной.

Примечание. Угловой коэффициент касательной может быть найден проще, если учащимся известно соотношение коэффициентов перпендикулярных прямых k₁•k₂ = – 1.

VI. Решение заданий в группах. (Приложение)

VII. Подведение итогов.

1. Ответьте на вопросы:

• Что называется касательной к графику функции в точке?

• В чем заключается геометрический смысл производной?

• Сформулируйте алгоритм нахождения уравнения касательной?

2. В чем были трудности на уроке, какие моменты урока наиболее понравились?

3. Выставление отметок.

 Задачи для самостоятельного решения в группах (часть задач можно использовать для домашнего задания).

1. Напишите уравнения касательных, проведенных к графику функции y = 2x² – 4x + 3 в точках пересечения графика с прямой y = x + 3.

Ответ: y = – 4x + 3, y = 6x – 9,5.

2. При каких значениях a касательная, проведенная к графику функции y = x² – ax в точке графика с абсциссой x₀ = 1, проходит через точку M(2; 3)?

Ответ: a = 0,5.

3. При каких значениях p прямая y = px – 5 касается кривой y = 3x² – 4x – 2?

Ответ: p₁ = – 10, p₂ = 2.

4. Найдите все общие точки графика функции y = 3x – x³ и касательной, проведенной к этому графику через точку P(0; 16).

Ответ: A(2; – 2), B(– 4; 52).

5. Найдите кратчайшее расстояние между параболой y = x² + 6x + 10 и прямой

Ответ:

6. На кривой y = x² – x + 1 найдите точку, в которой касательная к графику параллельна прямой y – 3x + 1 = 0.

Ответ: M(2; 3).

7. Напишите уравнение касательной к графику функции y = x² + 2x – | 4x |, которая касается его в двух точках. Сделайте чертеж.

Ответ: y = 2x – 4.

8. Докажите, что прямая y = 2x – 1 не пересекает кривую y = x⁴ + 3x² + 2x. Найдите расстояние между их ближайшими точками.

Ответ:

9. На параболе y = x² взяты две точки с абсциссами x₁ = 1, x₂ = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей? Напишите уравнения секущей и касательной.

Ответ: y = 4x – 3 – уравнение секущей; y = 4x – 4 – уравнение касательной.

10. Найдите угол q между касательными к графику функции y = x³ – 4x² + 3x + 1, проведенными в точках с абсциссами 0 и 1.

Ответ: q = 45°.

11. В каких точках касательная к графику функции образует с осью Ox угол в 135°?

Ответ: A(0; – 1), B(4; 3).

12. В точке A(1; 8) к кривой проведена касательная. Найдите длину отрезка касательной, заключенного между осями координат.

Ответ:

13. Напишите уравнение всех общих касательных к графикам функций y = x² – x + 1 и y = 2x² – x + 0,5.

Ответ: y = – 3x и y = x.

14. Найдите расстояние между касательными к графику функции параллельными оси абсцисс.

Ответ:

15. Определите, под какими углами парабола y = x² + 2x – 8 пересекает ось абсцисс.

Ответ: q₁ = arctg 6, q₂ = arctg (– 6).

16. На графике функции найдите все точки, касательная в каждой из которых к этому графику пересекает положительные полуоси координат, отсекая от них равные отрезки.

Ответ: A(– 3; 11).

17. Прямая y = 2x + 7 и парабола y = x² – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N.

Ответ: K(1; – 9).

18. При каких значениях b прямая y = 9x + b является касательной к графику функции y = x³ – 3x + 15?

Ответ: – 1; 31.

19. При каких значениях k прямая y = kx – 10 имеет только одну общую точку с графиком функции y = 2x² + 3x – 2? Для найденных значений k определите координаты точки.

Ответ: k₁ = – 5, A(– 2; 0); k₂ = 11, B(2; 12).

20. При каких значениях b касательная, проведенная к графику функции y = bx³ – 2x² – 4 в точке с абсциссой x₀ = 2, проходит через точку M(1; 8)?

Ответ: b = – 3.

21. Парабола с вершиной на оси Ox касается прямой, проходящей через точки A(1; 2) и B(2; 4), в точке B. Найдите уравнение параболы.

Ответ:

22. При каком значении коэффициента k парабола y = x² + kx + 1 касается оси Ox?

Ответ: k = д 2.

23. Найдите углы между прямой y = x + 2 и кривой y = 2x² + 4x – 3.

Ответ:

24. Определите, под какими углами пересекаются графики функций y = 2x² + 3x – 3 и y = x² + 2x + 3.

Ответ:

25. При каком значении k угол между кривыми y = x² + 2x + k и y = x² + 4x + 4 будет равен 45°?

Ответ: k = – 3.

26. Найдите все значения x0, при каждом из которых касательные к графикам функции y = 5cos 3x + 2 и y = 3cos 5x в точках в абсциссой x₀ параллельны.

Ответ:

27. Под каким углом видна окружность x² + y² = 16 из точки (8; 0)?

Ответ:

28. Найдите геометрическое место точек, из которых парабола y = x² видна под прямым углом?

Ответ: прямая

29. Найдите расстояние между касательными к графику функции образующими с положительным направлением оси Ox угол 45°.

Ответ:

30. Найдите геометрическое место вершин всех парабол вида y = x² + ax + b, касающихся прямой y = 4x – 1.

Ответ: прямая y = 4x + 3.