Цели урока:
1. Проведение краткого обзора изученного с 7 - го по 10 классы о составлении уравнения прямой и об условиях ее расположения в декартовой системе координат; выведения уравнения касательной к графику функции и формирование умения находить его для конкретных функций.
2. Развитие логического мышления, исследовательских навыков, функционального мышления, математической речи.
3. Выработка коммуникативных навыков в работе, способствование развитию самостоятельной деятельности учащихся.
Ход урока:
- Организационный момент:
- Ребята, мы научились с вами находить производные простых и сложных функций и, наконец, изучили геометрический и физический смысл производной функции в точке. Сегодня мы должны по ходу урока проверить полученные вами знания по пройденным темам, провести краткий обзор изученного с 7 по 10 классы о составлении уравнений прямых и об условиях их расположения в декартовой системе координат, и, наконец, вывести уравнение касательной к графику функции в заданной точке.
- Актуализация опорных знаний.
Опрос материала по карточкам (задания выполняются на доске)
1 ученик. Заполнить таблицу производных элементарных функций
2 ученик. Вспомни правила дифференцирования
Смотрите документ
3 ученик. Составьте уравнение прямой y=kx+4, проходящей через точку А(3; - 2)
4 ученик. Составьте уравнение прямой y=3x+b, проходящей через точку C(4; 2)
Дополнительные вопросы:
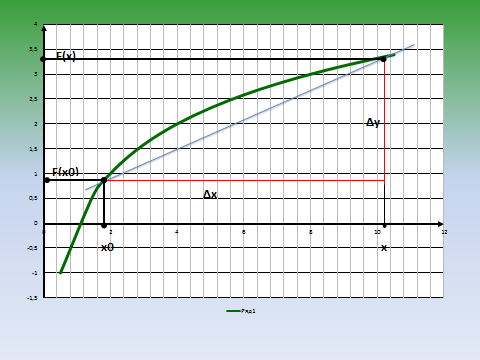
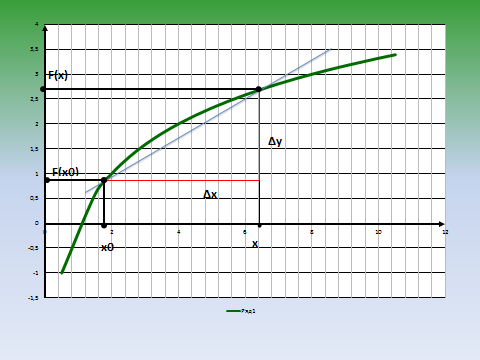
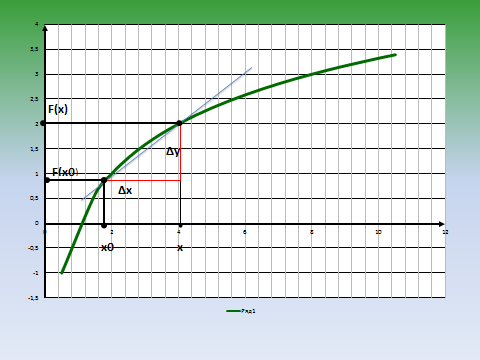
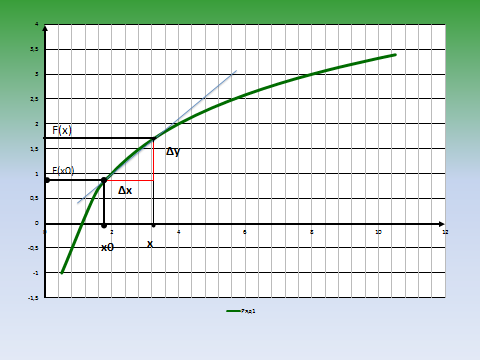
1. Через две точки графика функции (точку (х₀;у₀) и точку (х₀+∆х; у₀+∆у)) проведена секущая. В чем заключается геометрический смысл отношения приращения функции к приращению аргумента? ( слайд 1)
- Сформулируйте определение производной.
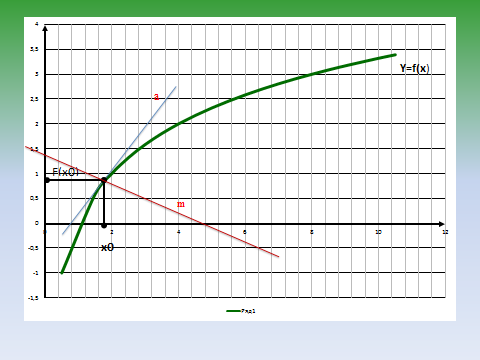
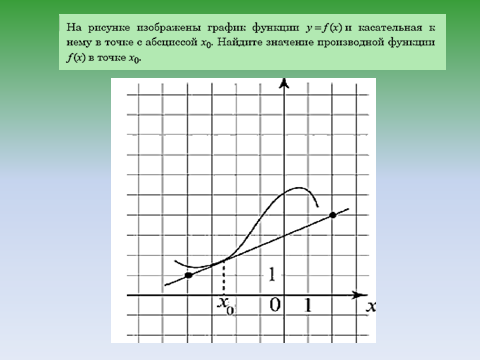
- В чем заключается геометрический смысл производной? (слайды 4 - 8)
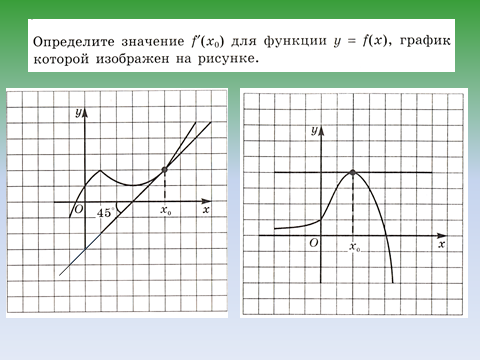
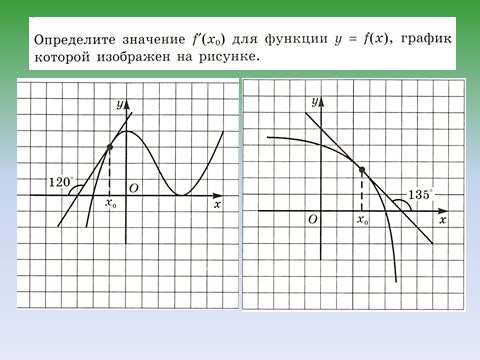
- Какой угол образует касательная с положительным направлением оси Ох, если f′(x)<0 (f′(x)˃0, f′(x)=0)?
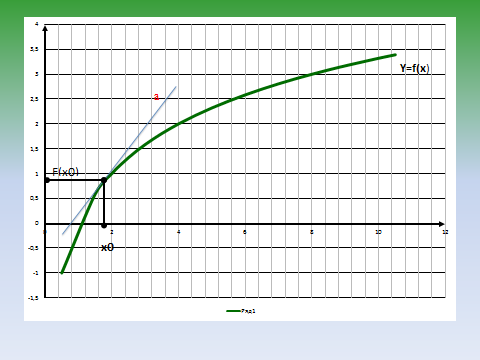
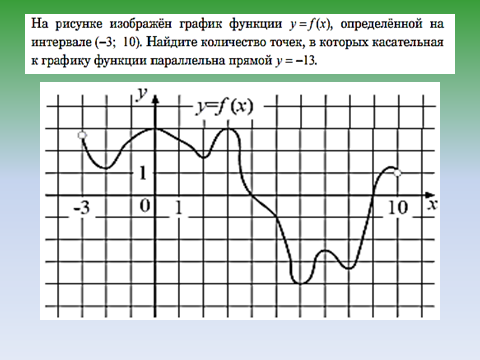
- Можно ли любую прямую, имеющую с графиком функции одну единственную точку назвать касательной к данному графику? (слайд 9)
- Работа со слайдами 10 - 13
- Ребята, а если бы задача звучала так:
Составить уравнение касательной , т. е. прямой, имеющей с графиком функции y=f(x) единственную точку (х₀;у₀) и образующую с положительным направлением оси Ох Это и есть основная задача нашего урока.
- Изучение новой темы
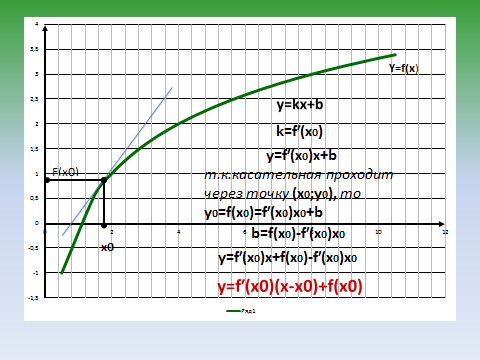
- Запишем тему урока «Уравнение касательной» и попробуем решить эту задачу в общем виде. (работа со слайдами 15 - 22)
- Запишем алгоритм составления уравнения касательной к графику функции в данной точке. (слайд 23)
- Решение опорных задач. (слайды 24 - 27)
- А теперь рассмотрим четыре типа опорных задач:
№1 Если задана абсцисса точки касания №824(б)
№2 По ординате точки касания№829
№3 Заданного направления № 835(а)
№4 Условия касания графика и прямой №842
- Подведение итога урока. (слайд 28)
- Задание на дом: 826(б), №832(а)№828

 Получите свидетельство
Получите свидетельство Вход
Вход



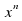
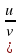 )′ =
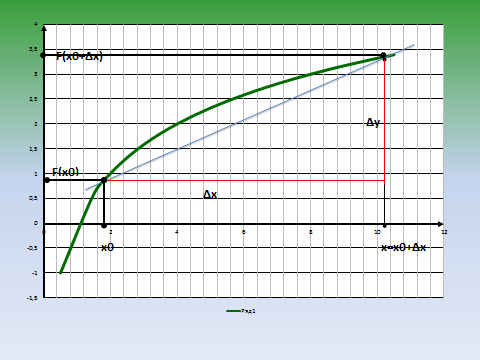
)′ =















 Урок математики на тему "Уравнение касательной" (0.62 MB)
Урок математики на тему "Уравнение касательной" (0.62 MB)
 0
0 770
770 104
104 Нравится
0
Нравится
0


