Угол между двумя плоскостями

Задания для подготовки подобраны с учетом того, что ученики хорошо владеют понятиями "Угол между прямыми", "Угол между прмой и плоскостью", "Угол между плоскостями".

Применяются различные формы контроля знаний и разноуровневые задания.

Угол между плоскостями Геометрия 10- 11 классы. Урок- повторение.

Тема. Угол между плоскостями.

• Основная цель.

• повторить определение угла
• повторить изученный ранее материал, необходимый при решении задач;
• рассмотреть решение задачи уровня С;
• вырабатывать навыки и умения решения задач на нахождение угла между плоскостями.

План урока.

• I. Организационный момент.
• II. Повторение: Математический диктант:
• 1).Определение двугранного угла.
• 2) Измерение двугранного угла.
• 3) Определение угла между плоскостями.
• 4) Теорема Пифагора.
• 5). Теорема косинусов.
• 6)определение тангенса угла в прямоугольном треугольнике.
• III. Демонстрация решения задач на нахождение угла
• между плоскостями уровня В 9 C 2 с помощью Geo Gebra Interaktiw
• Демонстрация решения задач на нахождение угла между плоскостями уровня С векторно-координатным методом и по определению.

• IV. Итоги урока. Задание на дом ( 2 уровневое).
•  

а

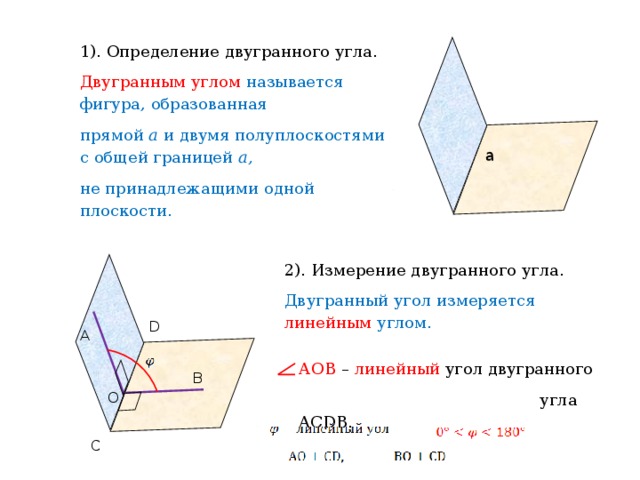
1). Определение двугранного угла.

Двугранным углом называется фигура, образованная

прямой а и двумя полуплоскостями с общей границей а,

не принадлежащими одной плоскости.

2). Измерение двугранного угла.

Двугранный угол измеряется линейным углом.

D

А

АОВ – линейный угол двугранного

угла ACDB.

В

О

С

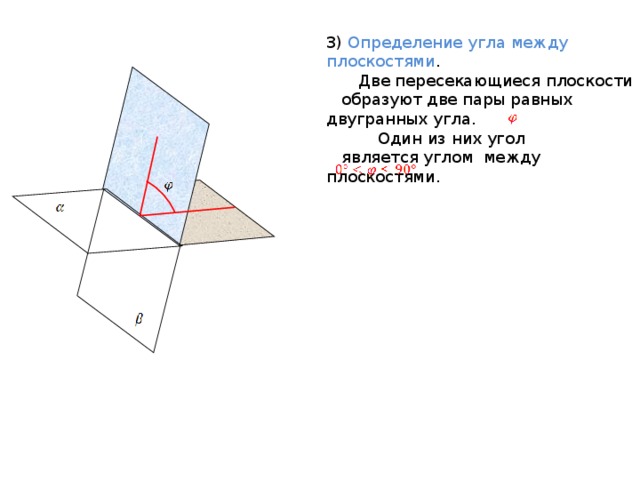
3) Определение угла между плоскостями .

Две пересекающиеся плоскости образуют две пары равных двугранных угла.

Один из них угол

является углом между плоскостями.

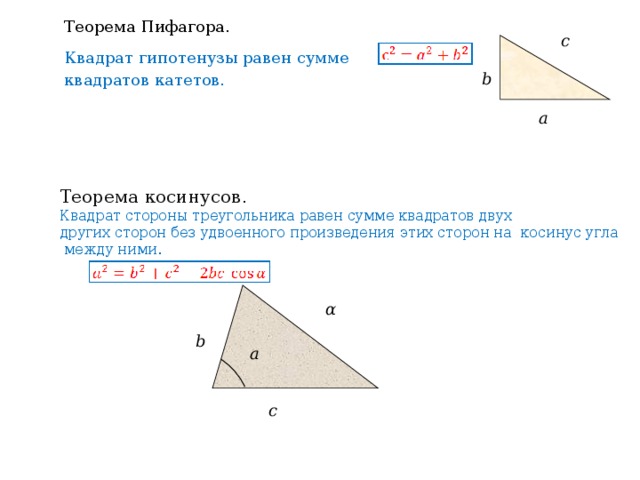
Теорема Пифагора.

Квадрат гипотенузы равен сумме квадратов катетов.

c

b

a

Теорема косинусов .

Квадрат стороны треугольника равен сумме квадратов двух

других сторон без удвоенного произведения этих сторон на косинус угла между ними.

α

b

a

c

Решение задач на нахождение угла между плоскостями уровня В 9.

I уровень

II уровень

• Высота правильной четырехугольной пирамиды равна 12, а сторона основания равна 8. Найдите тангенс угла между плоскостью боковой грани и плоскостью основания пирамиды.

• Сторона основания правильной четырехугольной пирамиды вдвое больше её высоты. Найдите угол между плоскостью боковой грани и плоскостью основания пирамиды. Ответ дайте в градусах.

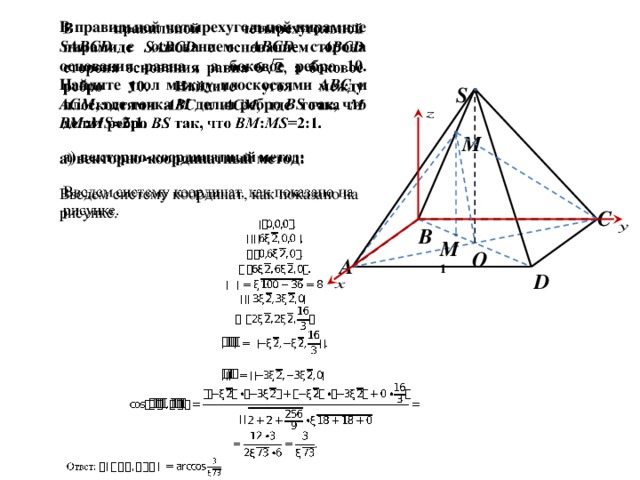
В правильной четырехугольной пирамиде SABCD c основанием ABCD сторона основания равна , а боковое ребро 10. Найдите угол между плоскостями АВС и АСМ , где точка М делит ребро BS так, что ВМ : МS =2:1.  

а) векторно-координатный метод:

Введем систему координат, как показано на рисунке.

S

M

C

B

M 1

O

A

D

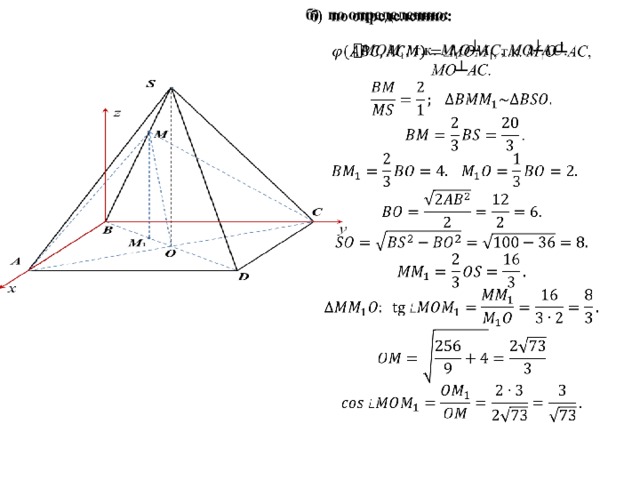
б) по определению:

 MОM 1 , т.к. М 1 О ┴ АС , МО ┴ АС .

Решить следующие задачи:

I вариант

IIвариант

• Основанием прямой треугольной призмы является равнобедренный треугольник АВС, в котором АВ=ВС=10, АС=16. Боковое ребро призмы равно 24. Точка Р-середина ребра .Найдите тангенс угла между плоскостями и АСР.
• Ответ: 2

• Сторона основания правильной треугольной призмы равна 2, а диагональ боковой грани равна . Найдите угол между плоскостью и плоскостью основания.
• Ответ:30