Вариант 1
И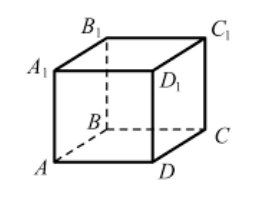 з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 10, её проекция равна 6, а угол между наклонной АС и плоскостью α равен 450.
з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 10, её проекция равна 6, а угол между наклонной АС и плоскостью α равен 450.
Ребро куба АВСDА1В1С1D1 равно 8. Найдите:
а) расстояние между прямыми ВВ1 и АC;
б) косинус между прямой А1С и плоскостью (АВС).
Через вершину Р равнобедренного треугольника КРЕ проведен к его плоскости перпендикуляр РО. Известно, что РО=16, КР=РЕ=13, КЕ=10. Найдите расстояние от точки О до прямой КЕ.
Вариант 2
И з точки М к плоскости α проведен перпендикуляр МС и наклонные МА и МВ. Найдите длину наклонной МА, если наклонная МВ = 13, её проекция равна 5, а угол между наклонной МА и плоскостью α равен 600.
з точки М к плоскости α проведен перпендикуляр МС и наклонные МА и МВ. Найдите длину наклонной МА, если наклонная МВ = 13, её проекция равна 5, а угол между наклонной МА и плоскостью α равен 600.
Ребро куба АВСDА1В1С1D1 равно 6. Найдите:
а) расстояние между прямыми СС1 и ВD;
б) синус между прямой В1D и плоскостью (АВС).
Через вершину А равнобедренного треугольника САЕ проведен к его плоскости перпендикуляр АВ. Известно, что АВ=6, СА=АЕ=17, СЕ=30. Найдите расстояние от точки А до прямой СЕ.
Вариант 3
И з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 15, её проекция равна 9, а угол между наклонной АС и плоскостью α равен 600.
з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 15, её проекция равна 9, а угол между наклонной АС и плоскостью α равен 600.
Ребро куба АВСDА1В1С1D1 равно 4. Найдите:
а) расстояние между прямыми ВВ1 и АC;
б) синус между прямой АС1 и плоскостью (АВС).
Через вершину R равнобедренного треугольника КRЕ проведен к его плоскости перпендикуляр RО. Известно, что RО=9, КR=RЕ=13, КЕ=10. Найдите расстояние от точки О до прямой КЕ.
Вариант 1
И з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 10, её проекция равна 6, а угол между наклонной АС и плоскостью α равен 450.
з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 10, её проекция равна 6, а угол между наклонной АС и плоскостью α равен 450.
Ребро куба АВСDА1В1С1D1 равно 8. Найдите:
а) расстояние между прямыми ВВ1 и АC;
б) косинус между прямой А1С и плоскостью (АВС).
Через вершину Р равнобедренного треугольника КРЕ проведен к его плоскости перпендикуляр РО. Известно, что РО=16, КР=РЕ=13, КЕ=10. Найдите расстояние от точки О до прямой КЕ.
Вариант 2
И з точки М к плоскости α проведен перпендикуляр МС и наклонные МА и МВ. Найдите длину наклонной МА, если наклонная МВ = 13, её проекция равна 5, а угол между наклонной МА и плоскостью α равен 600.
з точки М к плоскости α проведен перпендикуляр МС и наклонные МА и МВ. Найдите длину наклонной МА, если наклонная МВ = 13, её проекция равна 5, а угол между наклонной МА и плоскостью α равен 600.
Ребро куба АВСDА1В1С1D1 равно 6. Найдите:
а) расстояние между прямыми СС1 и ВD;
б) синус между прямой В1D и плоскостью (АВС).
Через вершину А равнобедренного треугольника САЕ проведен к его плоскости перпендикуляр АВ. Известно, что АВ=6, СА=АЕ=17, СЕ=30. Найдите расстояние от точки А до прямой СЕ.
Вариант 3
И з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 15, её проекция равна 9, а угол между наклонной АС и плоскостью α равен 600.
з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 15, её проекция равна 9, а угол между наклонной АС и плоскостью α равен 600.
Ребро куба АВСDА1В1С1D1 равно 4. Найдите:
а) расстояние между прямыми ВВ1 и АC;
б) синус между прямой АС1 и плоскостью (АВС).
Через вершину R равнобедренного треугольника КRЕ проведен к его плоскости перпендикуляр RО. Известно, что RО=9, КR=RЕ=13, КЕ=10. Найдите расстояние от точки О до прямой КЕ.
Вариант 1
И з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 10, её проекция равна 6, а угол между наклонной АС и плоскостью α равен 450.
з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 10, её проекция равна 6, а угол между наклонной АС и плоскостью α равен 450.
Ребро куба АВСDА1В1С1D1 равно 8. Найдите:
а) расстояние между прямыми ВВ1 и АC;
б) косинус между прямой А1С и плоскостью (АВС).
Через вершину Р равнобедренного треугольника КРЕ проведен к его плоскости перпендикуляр РО. Известно, что РО=16, КР=РЕ=13, КЕ=10. Найдите расстояние от точки О до прямой КЕ.
Вариант 2
И з точки М к плоскости α проведен перпендикуляр МС и наклонные МА и МВ. Найдите длину наклонной МА, если наклонная МВ = 13, её проекция равна 5, а угол между наклонной МА и плоскостью α равен 600.
з точки М к плоскости α проведен перпендикуляр МС и наклонные МА и МВ. Найдите длину наклонной МА, если наклонная МВ = 13, её проекция равна 5, а угол между наклонной МА и плоскостью α равен 600.
Ребро куба АВСDА1В1С1D1 равно 6. Найдите:
а) расстояние между прямыми СС1 и ВD;
б) синус между прямой В1D и плоскостью (АВС).
Через вершину А равнобедренного треугольника САЕ проведен к его плоскости перпендикуляр АВ. Известно, что АВ=6, СА=АЕ=17, СЕ=30. Найдите расстояние от точки А до прямой СЕ.
Вариант 3
И з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 15, её проекция равна 9, а угол между наклонной АС и плоскостью α равен 600.
з точки А к плоскости α проведен перпендикуляр АМ и наклонные АВ и АС. Найдите длину наклонной AС, если наклонная АВ = 15, её проекция равна 9, а угол между наклонной АС и плоскостью α равен 600.
Ребро куба АВСDА1В1С1D1 равно 4. Найдите:
а) расстояние между прямыми ВВ1 и АC;
б) синус между прямой АС1 и плоскостью (АВС).
Через вершину R равнобедренного треугольника КRЕ проведен к его плоскости перпендикуляр RО. Известно, что RО=9, КR=RЕ=13, КЕ=10. Найдите расстояние от точки О до прямой КЕ.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Угол между прямой и плоскостью (24.23 KB)
Угол между прямой и плоскостью (24.23 KB)
 0
0 250
250 4
4 Нравится
0
Нравится
0




