Цилиндр

Презентация по геометрии по теме "Цилиндр" включает в себя 43 слайда к темам уроков: Понятие о телах вращения, Прямой круговой цилиндр и его элементы, Осевое сечение цилиндра. Сечения цилиндра плоскостью, параллельной и перпендикулярной оси, Площадь боковой поверхности цилиндра, Площадь полной поверхности цилиндра, Объём цилиндра, Решение задач 

ЦИЛИНДР

Тема

A

http://lapinagv.jimdo.com/

Понятие о телах вращения.

Тема урока

http://lapinagv.jimdo.com/

• Говорят, что фигура Ф в пространстве получена вращением фигуры F вокруг оси а , если точки фигуры Ф получаются всевозможными поворотами точек фигуры F вокруг оси а . Фигура Ф при этом называется фигурой вращения .

Вращение точки А вокруг прямой а – окружность .

Вращение окружности вокруг её диаметра – сфера .

Вращение прямоугольника вокруг одной из его сторон – цилиндр .

http://lapinagv.jimdo.com/

Вращение трапеции, один из углов которой является прямым, вокруг боковой стороны – усечённый конус .

Вращение прямоугольного треугольника вокруг одного из катетов – конус .

Вращение окружности вокруг прямой, лежащей в плоскости окружности и не имеющей с этой окружностью общих точек – тор .

http://lapinagv.jimdo.com/

Вращение эллипса вокруг его оси– эллипсоид вращения .

Вращение параболы вокруг её оси – параболоид вращения .

Вращение гиперболы вокруг её оси – гиперболоид вращения .

http://lapinagv.jimdo.com/

http://lapinagv.jimdo.com/

Прямой круговой цилиндр и его элементы.

Тема урока

http://lapinagv.jimdo.com/

Цилиндр -

это тело вращения, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

http://lapinagv.jimdo.com/

Примеры цилиндров

Слово цилиндр - означает от греческого слова “ валик ”, “ каток ”.

http://lapinagv.jimdo.com/

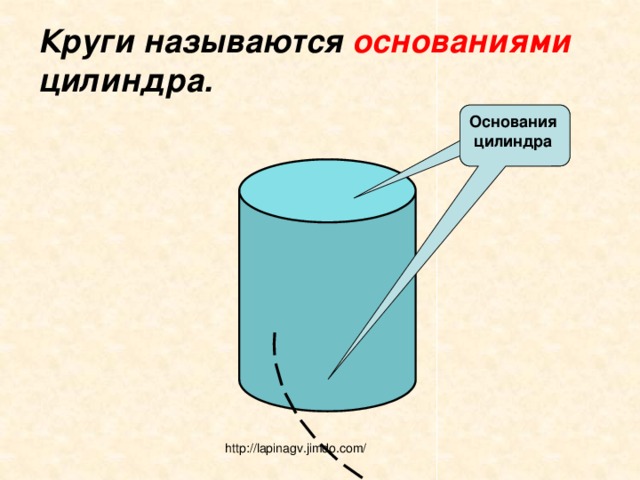
Круги называются основаниями цилиндра.

Основания

цилиндра

http://lapinagv.jimdo.com/

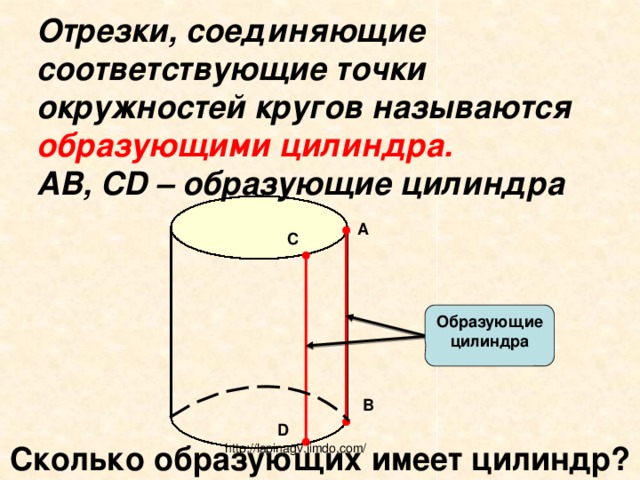
Отрезки, соединяющие соответствующие точки окружностей кругов называются образующими цилиндра. AB, CD – образующие цилиндра

A

C

Образующие

цилиндра

B

D

Сколько образующих имеет цилиндр?

http://lapinagv.jimdo.com/

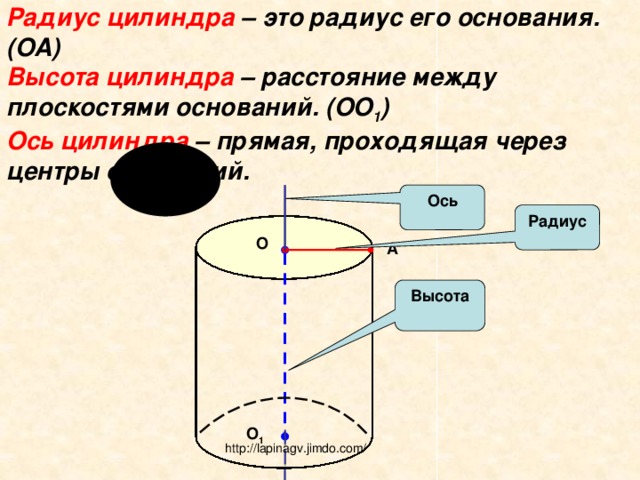
Радиус цилиндра – это радиус его основания.(OA) Высота цилиндра – расстояние между плоскостями оснований. (ОО 1 ) Ось цилиндра – прямая, проходящая через центры оснований.

Ось

Радиус

O

A

Высота

O 1

http://lapinagv.jimdo.com/

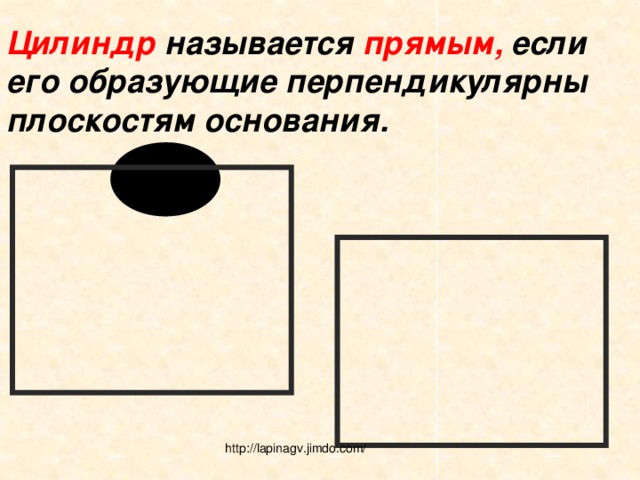
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания.

http://lapinagv.jimdo.com/

Высота цилиндра

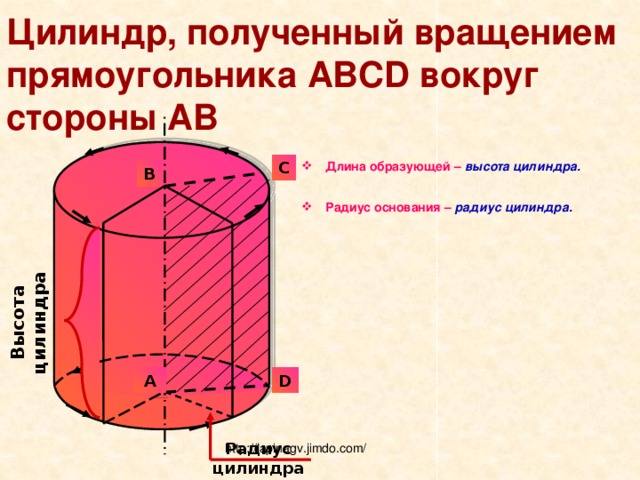
Цилиндр, полученный вращением прямоугольника ABCD вокруг стороны AB

• Длина образующей – высота цилиндра.

• Радиус основания – радиус цилиндра.

C

B

A

D

Радиус цилиндра

http://lapinagv.jimdo.com/

Осевое сечение цилиндра. Сечения цилиндра плоскостью, параллельной и перпендикулярной оси.

Тема урока

http://lapinagv.jimdo.com/

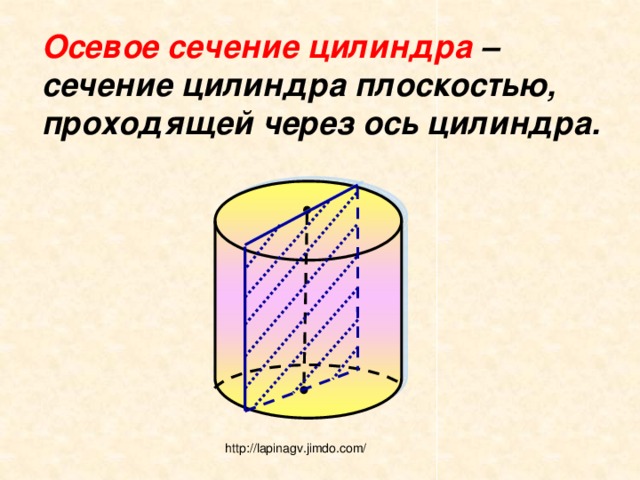
Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра.

http://lapinagv.jimdo.com/

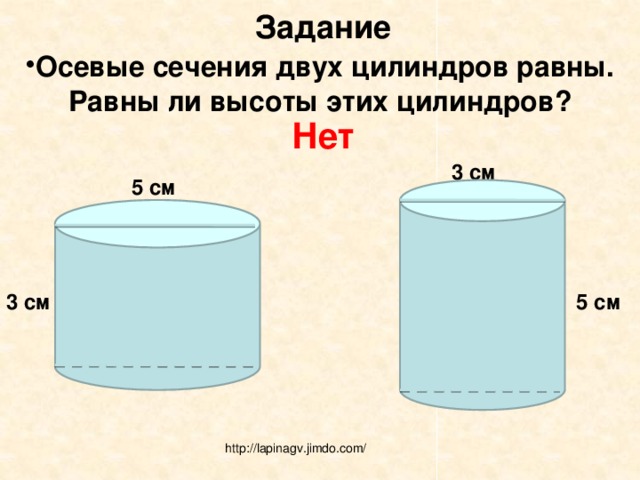
Задание

• Осевые сечения двух цилиндров равны. Равны ли высоты этих цилиндров?

Нет

3 см

5 см

5 см

3 см

http://lapinagv.jimdo.com/

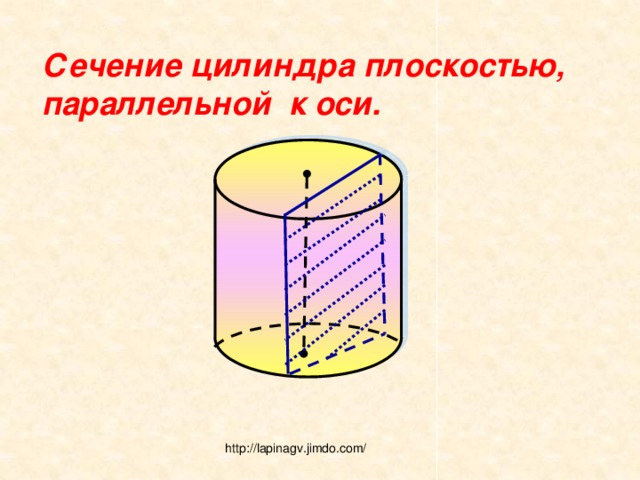
Сечение цилиндра плоскостью, параллельной к оси.

http://lapinagv.jimdo.com/

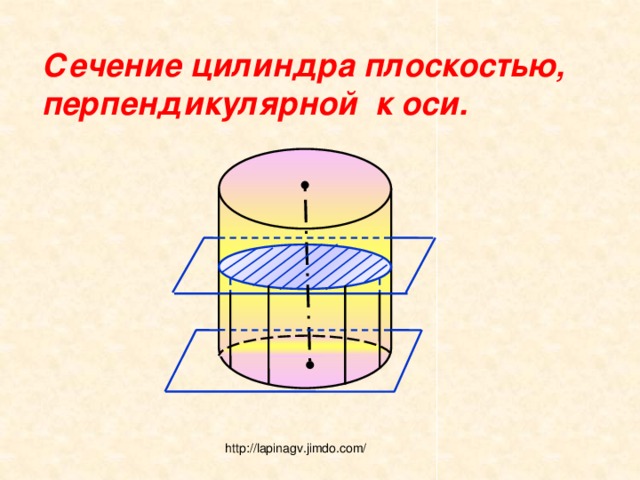
Сечение цилиндра плоскостью, перпендикулярной к оси.

http://lapinagv.jimdo.com/

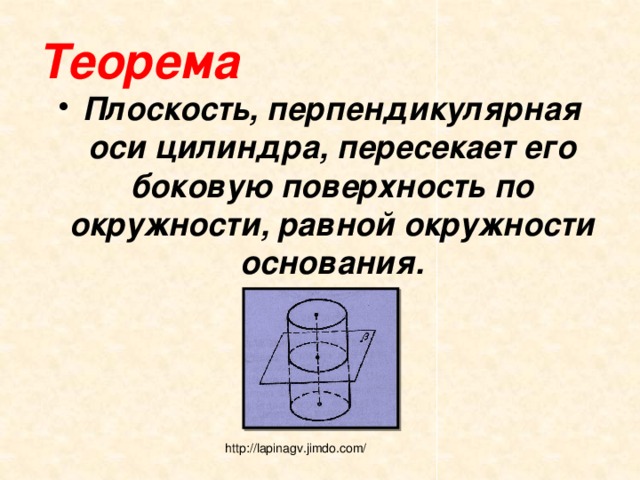
Теорема

• Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

http://lapinagv.jimdo.com/

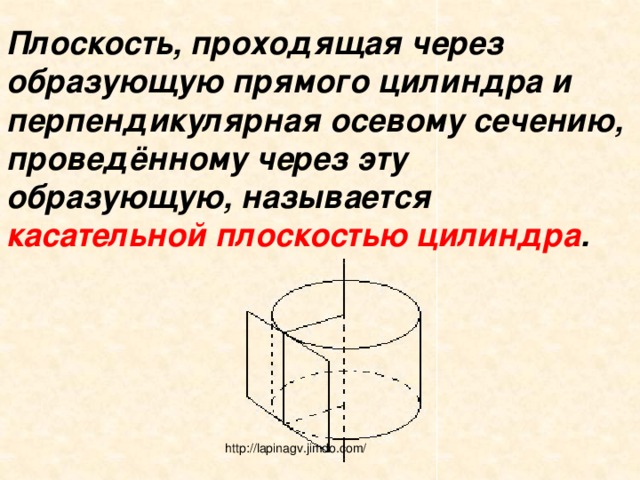
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра .

http://lapinagv.jimdo.com/

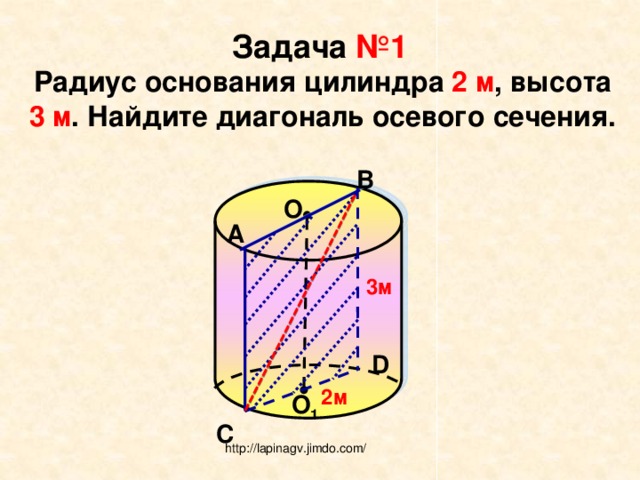
Задача №1

Радиус основания цилиндра 2 м , высота 3 м . Найдите диагональ осевого сечения.

В

О

А

3м

D

2м

О 1

С

http://lapinagv.jimdo.com/

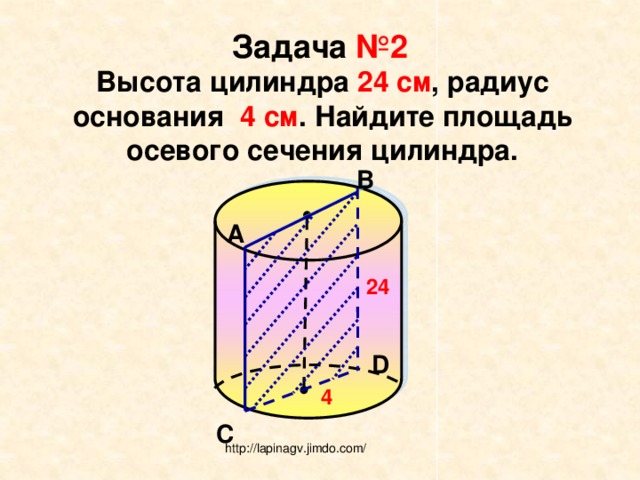
Задача №2

Высота цилиндра 24 см , радиус основания 4 см . Найдите площадь осевого сечения цилиндра.

В

А

24

D

4

С

http://lapinagv.jimdo.com/

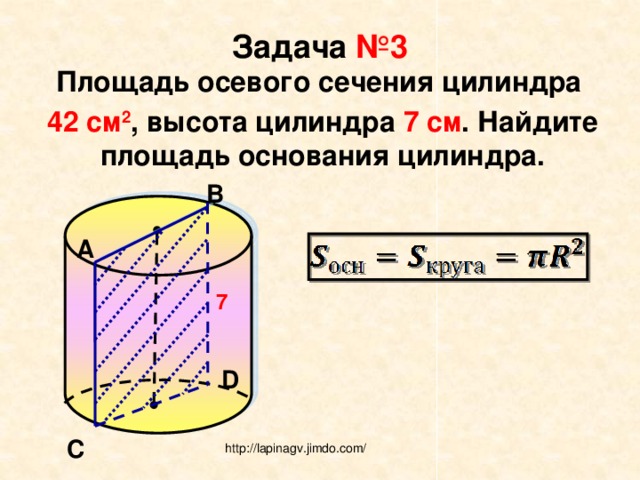
Задача №3

Площадь осевого сечения цилиндра

42 см 2 , высота цилиндра 7 см . Найдите площадь основания цилиндра.

В

А

7

D

С

http://lapinagv.jimdo.com/

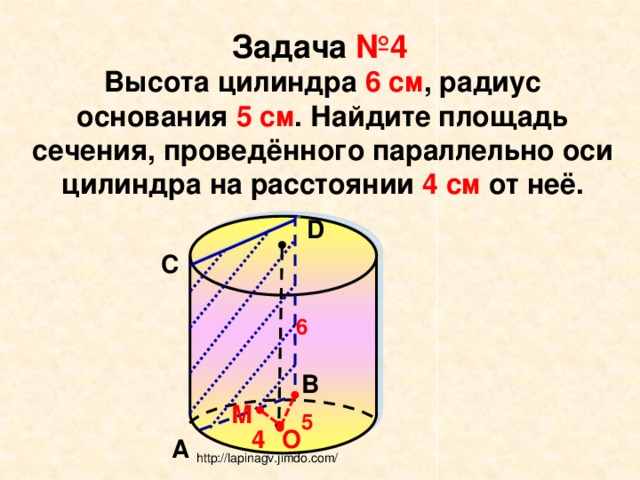
Задача №4

Высота цилиндра 6 см , радиус основания 5 см . Найдите площадь сечения, проведённого параллельно оси цилиндра на расстоянии 4 см от неё.

D

С

6

В

М

5

О

4

А

http://lapinagv.jimdo.com/

Площадь боковой поверхности цилиндра

Тема урока

http://lapinagv.jimdo.com/

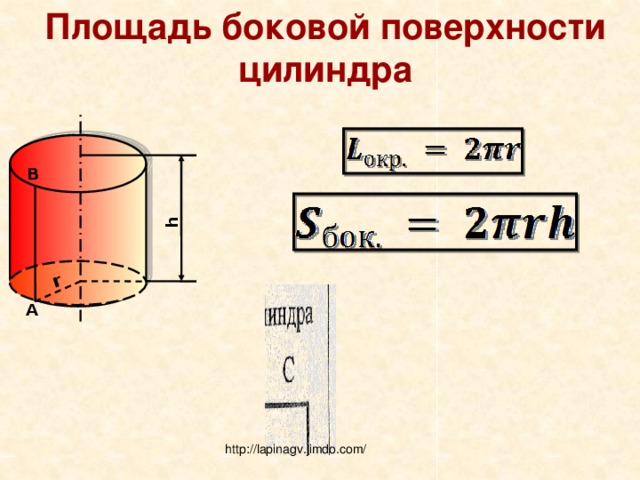
Площадь боковой поверхности цилиндра

r

h

B

A

http://lapinagv.jimdo.com/

Задание №1

• Точки А и В расположены на видимой части боковой поверхности цилиндра. Скопируйте рисунок и проведите отрезок АВ. Все ли точки отрезка АВ принадлежат боковой поверхности цилиндра?

http://lapinagv.jimdo.com/

Задание №2

• Точки А и В лежат соответственно на нижнем и на верхнем основаниях цилиндра, изображённого на рисунке. Скопируйте рисунок и проведите отрезок АВ. Определите, все ли точки отрезка АВ лежат на поверхности цилиндра.

http://lapinagv.jimdo.com/

Площадь полной поверхности цилиндра

Тема урока

http://lapinagv.jimdo.com/

Площадь полной поверхности цилиндра

r

h

B

A

http://lapinagv.jimdo.com/

Задача

• Осевое сечение цилиндра – квадрат , диагональ которого равна 20 см . Найдите:

• Высоту цилиндра;
• Площадь основания цилиндра;
• Площадь боковой поверхности;
• Площадь полной поверхности цилиндра.

http://lapinagv.jimdo.com/

Объём цилиндра

Тема урока

http://lapinagv.jimdo.com/

Призма, вписана в цилиндр, если её основания вписаны в основания цилиндра.

Призма, описана около цилиндра, если её основания описаны около оснований цилиндра.

Объём цилиндра равен произведению площади основания на высоту:

V = S осн H = πR 2 H

http://lapinagv.jimdo.com/

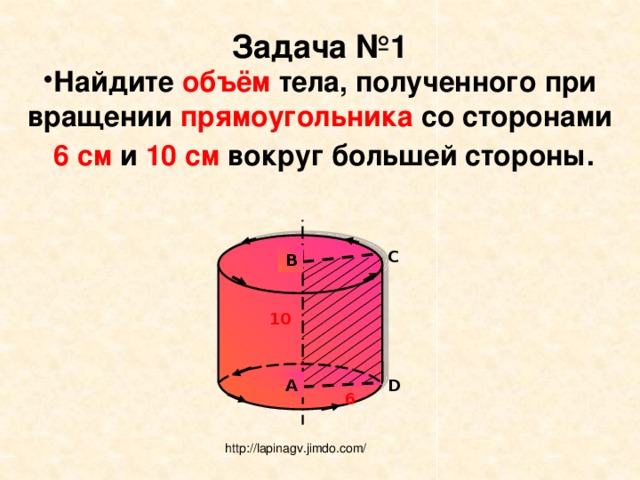
Задача №1

• Найдите объём тела, полученного при вращении прямоугольника со сторонами

6 см и 10 см вокруг большей стороны.

C

B

10

A

D

6

http://lapinagv.jimdo.com/

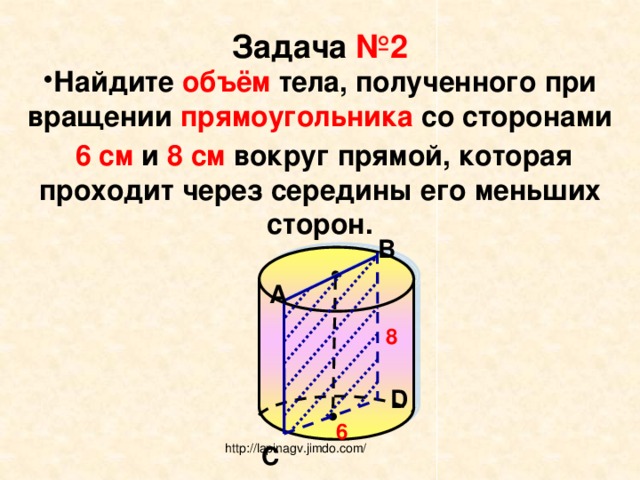
Задача №2

• Найдите объём тела, полученного при вращении прямоугольника со сторонами

6 см и 8 см вокруг прямой, которая проходит через середины его меньших сторон.

В

А

8

D

6

С

http://lapinagv.jimdo.com/

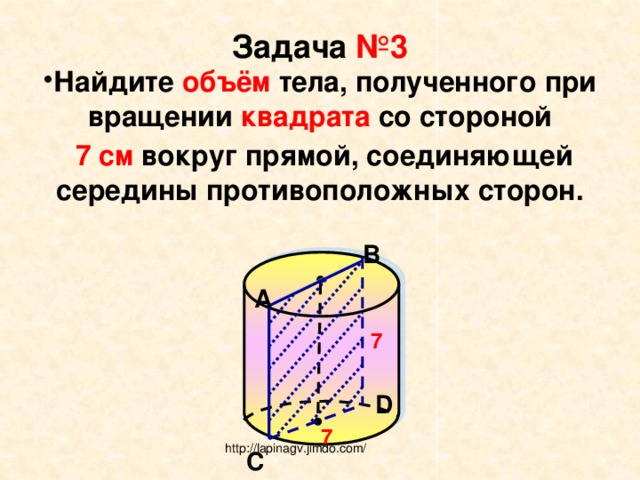
Задача №3

• Найдите объём тела, полученного при вращении квадрата со стороной

7 см вокруг прямой, соединяющей середины противоположных сторон.

В

А

7

D

7

http://lapinagv.jimdo.com/

С

Задача №4

• Свинцовая труба (плотность 11,4 г/см3 ) имеет длину 5м . Масса 200г . Найдите диаметр.

V= m: ρ

http://lapinagv.jimdo.com/

Решение задач

Тема урока

http://lapinagv.jimdo.com/

Задача №1

• Радиус основания цилиндра равен 4см , площадь боковой поверхности вдвое больше площади основания. Найдите объём цилиндра.

A

D

4

http://lapinagv.jimdo.com/

Задача №2

• Радиус основания цилиндра равен 6см , высота в 2 раза меньше длины окружности основания. Найдите площадь полной поверхности цилиндра.

A

D

6

http://lapinagv.jimdo.com/

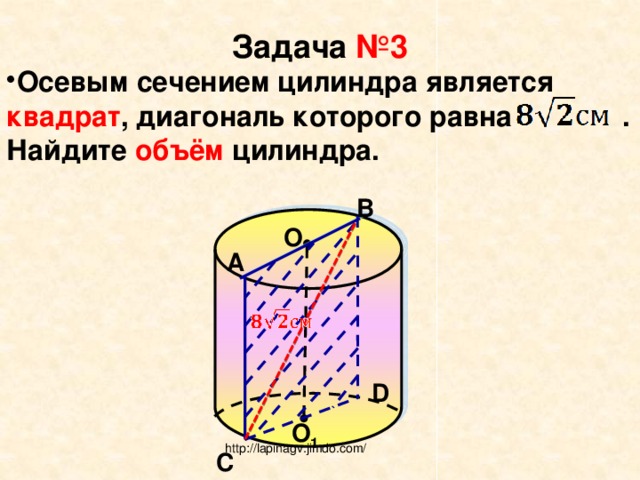
Задача №3

• Осевым сечением цилиндра является квадрат , диагональ которого равна . Найдите объём цилиндра.

В

О

А

D

О 1

http://lapinagv.jimdo.com/

С

Задача №4

• Отрезок, соединяющий конец диаметра нижнего основания цилиндра с центром его верхнего основания, равен 2см и наклонён к плоскости основания под углом 30° . Найдите площадь полной поверхности цилиндра.

А

2

D

30°

О

http://lapinagv.jimdo.com/

С