
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Преподаватель математики
ФГКОУ СПб КК МО РФ
Корнилова И.Ф.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.
Пример 1.
Пусть
- п. к.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.
Пример 2.
Пусть
-п.к.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.
Пример 1.
Пусть
-п.к.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.
Пример 2.
-решений нет

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.
Пример 1.
Пусть
-п.к.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ.
Пример 2.
Пусть

Решить уравнение:

Рассмотрим другой способ решения:

Однородным тригонометрическим уравнением первой степени называется уравнение вида:
ОДНОРОДНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
где
Однородным тригонометрическим уравнением
второй степени называется уравнение вида:
где

ОДНОРОДНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Пример 1

ОДНОРОДНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Пример 2
Пусть

ОДНОРОДНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Пример 3
Пусть

УРАВНЕНИЯ ВИДА Asinx+Bcosx=C
Способ 1. С помощью формул двойного аргумента и основного тригонометрического
тождества привести к однородному уравнению второй степени.
Раскрыв скобки и приведя подобные слагаемые получаем:
Если
то это однородное уравнение
второй степени.

УРАВНЕНИЯ ВИДА Asinx+Bcosx=C
Пример 1.

УРАВНЕНИЯ ВИДА Asinx+Bcosx=C
Пример 2.
Не является однородным
уравнением! Разложить на
множители!

УРАВНЕНИЯ ВИДА Asinx+Bcosx=C
Способ 2. Метод введения вспомогательного
аргумента
Вынесем за скобки

Рассмотрим прямоугольный треугольник с
катетами длиной А и В.
Тогда длина гипотенузы
В
отсюда,
А
где
т.о. метод введения вспомогательного аргумента
удобно применять, если

УРАВНЕНИЯ ВИДА Asinx+Bcosx=C
Пример 1.

МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
Применение формул преобразования суммы
тригонометрических функций в произведение

МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
Пример 1.

МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
Пример 2.
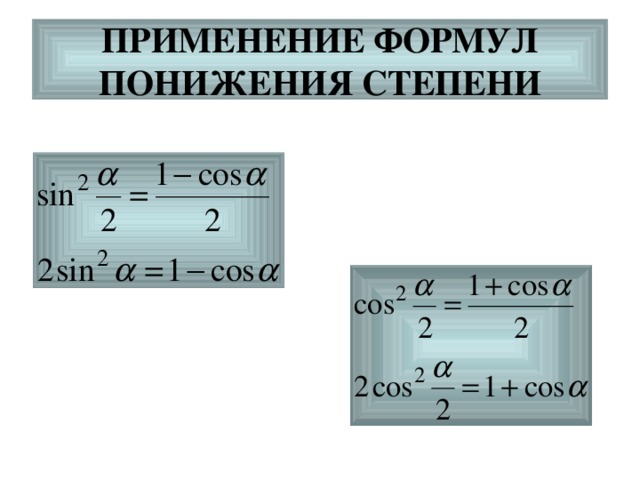
ПРИМЕНЕНИЕ ФОРМУЛ ПОНИЖЕНИЯ СТЕПЕНИ

ПРИМЕНЕНИЕ ФОРМУЛ ПОНИЖЕНИЯ СТЕПЕНИ
Пример 1.

ПРИМЕНЕНИЕ ФОРМУЛ ПОНИЖЕНИЯ СТЕПЕНИ
Пример 2

ПРИМЕНЕНИЕ СЛЕДСТВИЙ ИЗ ФОРМУЛ СЛОЖЕНИЯ

ПРИМЕНЕНИЕ СЛЕДСТВИЙ ИЗ ФОРМУЛ СЛОЖЕНИЯ
Пример 1.
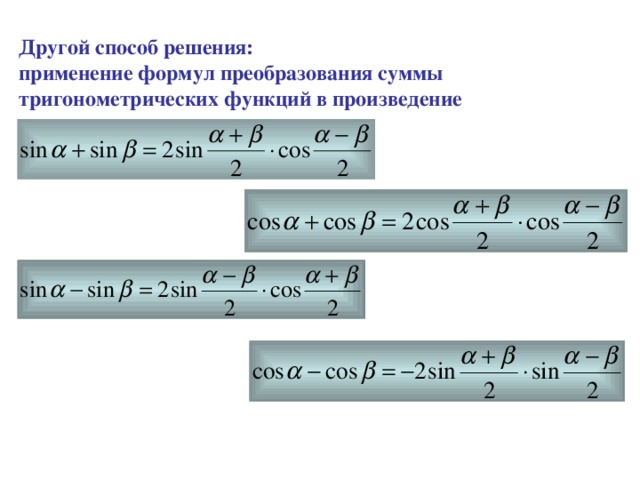
Другой способ решения:
применение формул преобразования суммы тригонометрических функций в произведение
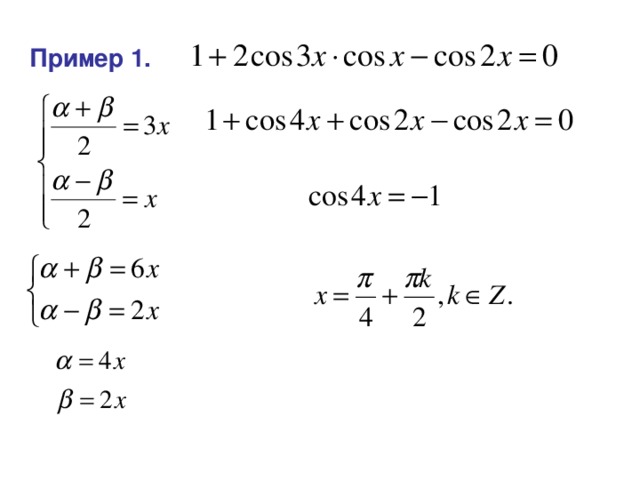
Пример 1.

Пример 2.
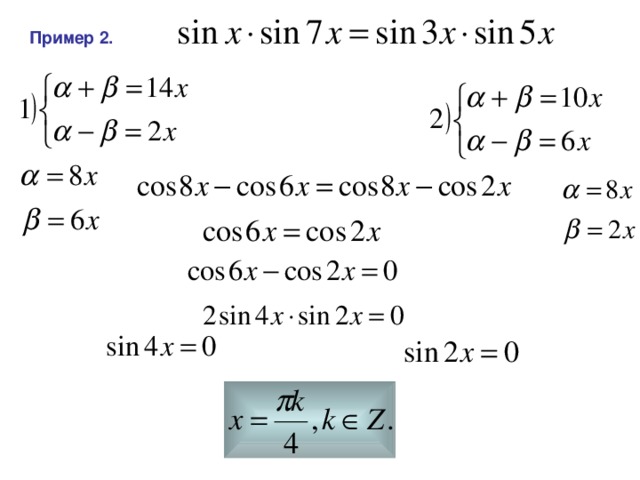
Пример 2.


 Получите свидетельство
Получите свидетельство Вход
Вход


































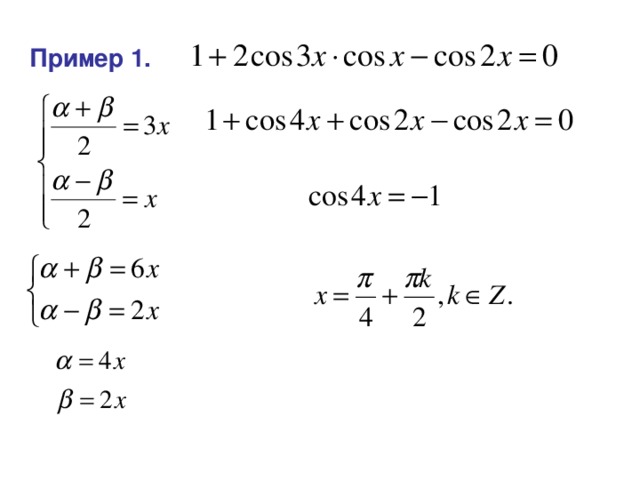

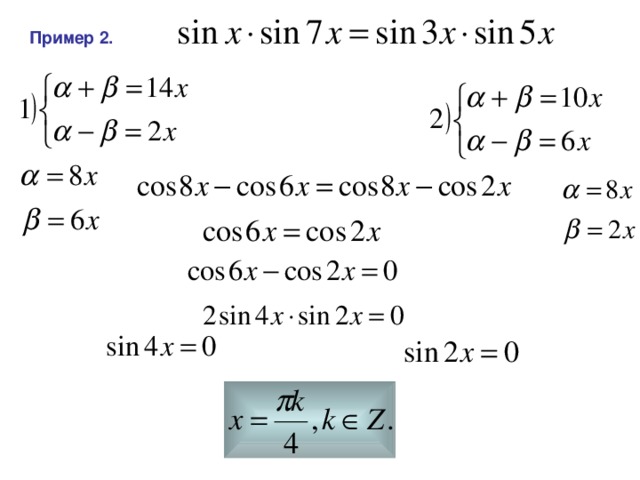









 Тригонометрические уравнения (0.81 MB)
Тригонометрические уравнения (0.81 MB)
 1
1 3032
3032 276
276 Нравится
0
Нравится
0




