
Работа выполнена
студенткой ГАПОУ КО «ОКТУ»
Группы ТУР-11-20
Зайцевой Александрой

Блез Паскаль – выдающийся математик, физик, механик, философ, литератор. Стоял у истоков основания математического анализа, теории вероятности и проективной геометрии, создал первую счетную машину, прототип современного калькулятора, сформулировал основной закон гидростатики, автор нескольких философских сочинений.
Разносторонний гений Блез Паскаль. Природа отвела ему всего 39 земных лет, большая часть из которых прошла в борьбе с болезнью, но он столько сделал для науки и литературы, сколько некоторым не удается за долгую жизнь. Он обладал уникальной способностью проникать в самую суть вещей, и благодаря этому стать одним из величайших мировых ученых. Его литературные творения бессмертны, в них содержатся его мысли, высказывания, цитаты. Паскаль твердо верил в бесконечность предмета познания, и утверждал, что познаниям нет конца.

Если числа
треугольника Паскаля
обладают особыми
свойствами,
то его
можно считать
волшебным.

" Треугольник Паскаля так прост,
что выписать его сможет даже
десятилетний ребенок.
В тоже время он таит в себе
неисчерпаемые сокровища и связывает
воедино различные аспекты математики,
не имеющие на первый взгляд между
собой ничего общего.
Столь необычные свойства позволяют
считать треугольник Паскаля одной из
наиболее изящных схем
во всей математике".
Мартин Гарднер
"Математические новеллы"
1974

ТРЕУГОЛЬНИК ПАСКАЛЯ
— это бесконечная числовая таблица
"треугольной формы", в которой по боковым
сторонам стоят единицы и всякое число,
кроме этих боковых единиц.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
. . . . . . . . . . . . . . .

Каждое число
равно сумме двух
расположенных
над ним чисел.
Треугольник можно продолжать неограниченно.
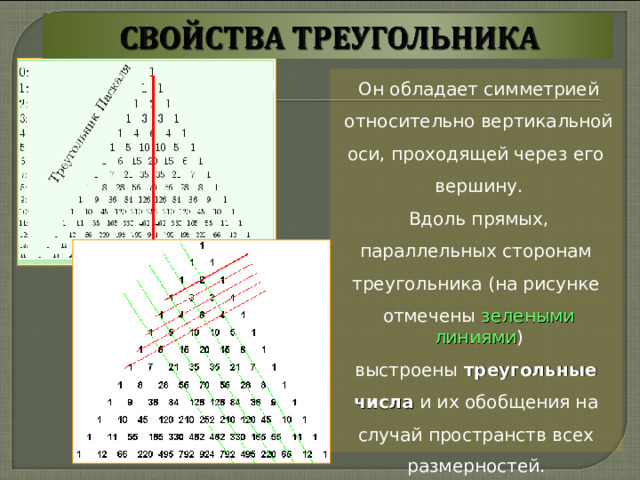
Он обладает симметрией
относительно вертикальной
оси, проходящей через его
вершину.
Вдоль прямых,
параллельных сторонам
треугольника (на рисунке
отмечены зелеными линиями )
выстроены треугольные
числа и их обобщения на
случай пространств всех
размерностей.

Треугольные числа показывают, сколько касающихся кружков можно расположить в виде треугольника
Классический пример начальная расстановка шаров в бильярде.
Треугольник Паскаля

Следующая зеленая
линия покажет нам
тетраэдральные числа
- один шар мы можем
положить на три –
итого четыре, под три
подложим шесть
- итого десять, и так
далее.

Следующая зеленая
линия продемонстрирует
попытку выкладывания
гипертетраэдра в
четырехмерном
пространстве - один шар
касается четырех, а
те, в свою очередь,
десяти...

Самая верхняя зелёная линия, на которой расположились числа натурального ряда - это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии - сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц - это тоже треугольные числа в нульмерном пространстве - сколько бы шаров мы не взяли - больше одного расположить не сможем, ибо просто негде - нет ни длины, ни ширины, ни высоты.

Заменим каждое число в
треугольнике Паскаля точкой.
Причем, нечетные точки
выведем контрастным цветом,
а четные - прозрачным, или
цветом фона.
Результат
окажется непредсказуемо-
удивительным: треугольник
Паскаля разобьется на более
мелкие треугольники,
образующие изящный узор.

Пусть, например, мы хотим
вычислить сумму чисел
натурального ряда от 1 до 9.
"Спустившись" по диагонали
До числа 9, мы увидим слева
снизу от него число 45 .
Оно то и дает искомую сумму.

Биномиальные коэффициенты есть
коэффициэнты разложения многочлена
по степеням x и y

Предположим , что некий шейх, следуя законам гостеприимства, решает отдать вам трех из семи своих жен. Сколько различных выборов вы можете сделать среди прекрасных обитательниц гарема ? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35.
Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не дает вам ошибиться!


 Получите свидетельство
Получите свидетельство Вход
Вход











 Треугольник паскаля (3.96 MB)
Треугольник паскаля (3.96 MB)
 0
0 1072
1072 54
54 Нравится
0
Нравится
0



