Урок №1. Тема: Выражения с переменными.
Цели урока:
Образовательные:
Развивающие:
развивать навыки устной и письменной речи, вычислительные навыки учащихся;
развивать у учащихся аккуратность оформления записей, интерес и любовь к предмету, память и мыслительные операции (анализ, синтез, обобщение, конкретизация и др.);
формировать умения чётко и ясно излагать свои мысли, задавать вопросы.
Воспитательные:
способствовать выявлению и раскрытию способностей учащихся;
воспитывать познавательную активность учащихся;
прививать самостоятельность и любознательность.
Ход урока:
Организационный момент.
Анализ контрольной работы.
Разобрать задания из контрольной работы, при решении которых было допущено наибольшее количество ошибок.
Изучение нового материала
Можно начать с небольшой лекции о развитии алгебры в различных частях света.
Вавилон. Истоки алгебры восходят к глубокой древности. Уже около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно - второй степени. С помощью таких уравнений решались разнообразные задачи землемерия, строительного искусства и военного дела.
Буквенные обозначения, применяемые нами в алгебре, не употреблялись вавилонянами; уравнения записывались в словесной форме.
Китай. За 2000 лет до нашего времени китайские ученые решали уравнения первой степени и их системы, а также квадратные уравнения. Им были знакомы отрицательные и иррациональные числа. Так как в китайском письме каждый знак изображает некоторое понятие, то в китайской алгебре не могло быть "сокращенных" обозначений.
В последующие эпохи китайская математика обогатилась новыми достижениями. Так в конце 13 века китайцы знали закон образования биноминальных коэффициентов, известный ныне под именем "треугольник Паскаля". В Западной Европе этот закон был открыт (Штифелем) на 250 лет позднее.
Страны арабского языка. Узбекистан. Таджикистан. У индийских авторов алгебраические вопросы излагались в астрономических сочинениях; самостоятельной дисциплиной алгебра становится у ученых, писавших на международном языке мусульманского мира - арабском. Основоположником алгебры, как особой науки нужно считать среднеазиатского ученого Мухаммеда из Хорезма, известного под арабским прозвищем Аль-Хоризми (Хорезмиенец). Его алгебраический труд, составленный в 9 в. н. э., носит название "Книга восстановления и противопоставления". "Восстановлением" Мухаммед называет перенос вычитаемого из одной части уравнения в другую, где оно становится слагаемым; "противопоставлением" - собирание неизвестных в одну сторону уравнения, а известных - в другую сторону. На арабском языке "восстановление" называется "ал-джебр". Отсюда и название "алгебра".
У Муххамеда Хорезмского и у последующих авторов алгебра широко применяется к купеческим и иным денежным расчетам. Ни он, ни другие математики, писавшие на арабском языке, не употребляли никаких сокращенных обозначений. (В них не было нужды, ибо арабское письмо очень кратко: гласные не обозначаются, согласные и полугласные буквы просты по начертанию и сливаются по нескольку в один знак.) Они не признавали и отрицательных чисел: учение об отрицательных числах, знакомое им из индийских источников, они считали плохо обоснованными. Это было справедливо, но зато индийские ученые могли ограничиться одним случаем полного квадратного уравнения, тогда как Мухаммед Хорезмский и его преемники должны были различать три случая (x2+px=q, x2+q=px, x2=px+q; p и q - положительные числа).
Средневековая Европа. В 12 веке "Алгебра" Аль-Хорезми стала известна в Европе и была переведена на латинский язык. С этого самого времени начинается развитие алгебры в европейских странах (сначала под сильным влиянием науки восточных народов). Появляются сокращенные обозначения неизвестных, решается ряд новых задач, связанных с потребностями торговли. Но существенного сдвига не было до 16 века. В первой трети 16 века итальянцы Дель-Ферро и Тарталья нашли правила для решения кубических уравнений вида x3=px+q; x3+px=q; x3+q=px. А Кардане в 1545 г. показал, что всякое кубическое уравнение сводится к одному из этих трех; в это же время Феррари, ученик Кардана, нашел решение уравнения четвертой степени.
Для объяснения новой темы на доске должны быть записаны выражения:
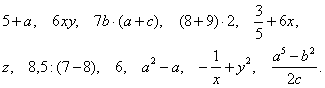
Ученики самостоятельно должны постараться выбрать из данных выражений буквенные. Те выражения, которые, по их мнению, не являются буквенными – зачеркиваются. Затем преподаватель дает определение буквенным выражениям и проверяет, насколько верно ученики выполнили задание. Так же вводится понятие переменной и рассказывается о сокращении записи в буквенных выражениях. После этого ученики по данным выражениям должны ответить на следующие вопросы.
Является ли данное выражение буквенным?
Сколько действий в данном выражении?
Сколько переменных содержится в данном выражении?
Какие переменные участвуют в записи?
Вычислить значение выражения, если вместо всех переменных подставить 2. (Для всех ли выражений достаточно замены одной переменной?)
Понятие рационального и целого выражения.
4. Закрепление нового материала.
Решить задания № 179, 180, 181, 182 (устно).
Решить письменно № 184, 185 (а), 186(а), 190 (а, б).
Самостоятельно №188.
Турист рухається зі швидкістю 5 км/год. Яку відстань він подолає за х годин?
На одній полиці лежить х зошитів, а на іншій на 3 зошити більше.
Скільки зошитів на другій полиці? На двох полицях разом?
Нотатник коштує х грн., а ручка — у грн. Купили 3 нотатники та
4 ручки. Скільки коштує ця покупка?
5. Итоги урока. Рефлексия.
6. Домашнее задание.
Прочитать, разобрать и выучить правила из § 5.
Решить задания № 185 (б), 186 (б), 189 (а, б), 187.
Урок №2. Тема: Числовое значение выражения.
Цели урока:
Образовательные
Развивающие
Воспитательные
Ход урока:
1. Организационный момент
Определение темы, целей и задач урока, плана работы на урок.
2. Мотивация урока.
Знаки «+» и « - » впервые употребил в записи немецкий математик Ян Видман.
Знаки « · » и « : » впервые использовал в 1684 году Готфрид Лейбниц.
Знак « = » ( равенства) был впервые введён английским математиком Робертом Рикордоном.
Как нет на свете без ножек столов,
Как нет на свете без рожек козлов,
Котов без усов и без панцирей раков,
Так нет в математике действий без знаков!
3. Актуализация опорных знаний. Проверка д/з.
Фронтальный опрос: Что называется буквенным выражением? Числовым выражением?
Какие выражения называются рациональными? Целыми? Привести примеры.
Как найти значение буквенного выражения?
Решить № 189 (б, г), 190 (в), 194, 196.
4. Нахождение числового значения выражений.
Решить №192, 197 (а, г), 196 (в), 203 (а).
5. Физкультминутка (выполнение упражнений для рук) .
Руки подняли и покачали –
Это деревья в лесу.
Руки нагнили, кисти встряхнули –
Ветер сбивает росу.
В сторону руки, плавно помашем –
Это к нам птицы летят.
Как они сели, тоже покажем –
Руки мы сложим – вот так.
6. Самостоятельная работа:
заполнить таблицу № 201.
7. Итоги урока.
8. Домашнее задание.
Решить: на 4 балла - №191, на 7 баллов - 198 (б, г), на 9 баллов - 203 (б), на 11 баллов - 204.
Урок №3. Тема: Тождества.
Цели урока:
Обучающая цель:
повторить определения уравнения, тождества;
научиться различать понятия уравнения и тождества;
выявить способы доказательства тождеств;
Развивающая цель:
развивать грамотную математическую речь учащихся (обогащать и усложнять словарный запас при использовании специальных математических терминов),
развивать мышление: умения сравнивать, анализировать, проводить аналогии, прогнозировать, делать выводы (при выборе способов доказательства тождеств);
Воспитательная цель:
Ход урока:
1. Организационный момент
Определение темы, целей и задач урока, плана работы на урок.
2. Мотивация урока.
3. Актуализация опорных знаний.
Дайте определение корня уравнения.
Что значит решить уравнение?
Что значит “равносильные уравнения”?
Сформулируйте свойства уравнений.
Дайте определение линейного уравнения.
Сколько корней может иметь линейное уравнение.
Сформулируйте переместительное, сочетательное, распределительное свойства действий над числами.
Какие выражения называются тождественно равными? Какое равенство называется тождеством? Приведи примеры.
4. Усвоение нового материала.
решить №214 (устно), 219, 221, 230 (б, г).
5. Самостоятельная работа.
Решить №222
6. Итоги урока. Рефлексия.
7. Домашнее задание.
Решить: выучить п.6, решить № 220, 227. 229.
Урок №4. Тема: Тождественные преобразования выражений.
Цели урока:
Обучающая цель:
повторить определения уравнения, тождества;
закрепить понятие тождества; способы доказательства тождеств;
Развивающая цель:
развивать грамотную математическую речь учащихся (обогащать и усложнять словарный запас при использовании специальных математических терминов), развивать мышление: умения сравнивать, анализировать, проводить аналогии, прогнозировать, делать выводы (при выборе способов доказательства тождеств);
Воспитательная цель:
Ход урока:
1. Организационный момент
Определение темы, целей и задач урока, плана работы на урок.
2. Мотивация урока.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте,
Все ль в порядке-
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Тут затеи и задачи,
Игры, шутки – все для вас!
Пожелаю всем удачи.
За работу, в добрый час!
3. Актуализация опорных знаний. Проверка домашнего задания.
Дайте определение корня уравнения.
Что значит решить уравнение?
Что значит “равносильные уравнения”?
Сформулируйте свойства уравнений.
Дайте определение линейного уравнения.
Сколько корней может иметь линейное уравнение.
Сформулируйте переместительное, сочетательное, распределительное свойства действий над числами.
Какие выражения называются тождественно равными? Какое равенство называется тождеством? Приведи примеры.
4. Закрепление навыков тождественных преобразований выражений.
решить №233, 235, 238.
5. Самостоятельная работа.
Вариант 1: № 236 (а)
Вариант 2: №2236 (б).
6. Итоги урока. Рефлексия.
7. Домашнее задание.
Решить: решить № 237, 234, 239.
Урок №5. Тема: Степень с натуральным показателем.
Цели урока:
изучить понятие степени и правила вычисления степени с натуральным показателем;
развивать у учащихся навыки вычисления степеней и решения примеров с использованием степени;
воспитывать ответственное отношение к учебному труду, учить преодолевать трудности, формировать навыки сотрудничества, расширение кругозора знаний.
Ход урока:
1. Организационный момент.
2. Мотивация урока.
Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя. А начать наш урок я хотела бы с выяснения вопроса: встречался кто-нибудь из вас в повседневной жизни со словом «степень»? Давайте приведем примеры словосочетаний из жизни, в которых оно используется, и попытаемся с их помощью разобраться, что же в жизни означает слово «степень».
точности
Степень усвоения
качества
знаний
Каким же близким по смыслу словом можно заменить слово “степень”?
А где мы можем уточнить его значение? (в толковом словаре)
Степень – это мера, сравнительная величина; уровень чего-нибудь.
Слово “степень” находит широкое применение и в математике.
3.Актуализация опорных знаний.
Пригадаємо відоме українське прислів’я : «Знання збираються по краплині, як вода в долині.» И соберём по капельке всё, что учили по теме: «Степень» в младших класах.
Дайте определение степени с натуральным показателем. (Степенью числа а с натуральным показателем п, большим 1, называется произведение п множителей, каждый из которых равен а.)
Как называется число, которое возводим в степень? (Число, которое возводим в степень, называют основанием)
Как называется число, в которое возводим степень? (Число, в которое возводим степень, называют показателем)
Какое число получаем при возведении в степень положительного числа? (При возведении в степень положительного числа получаем положительное число)
Какое число получаем при возведении отрицательного числа с четным показателем? (При возведении отрицательного числа с четным показателем получаем положительное число)
Какое число получаем при возведении отрицательного числа с нечетным показателем? (При возведении отрицательного числа с нечетным показателем получаем отрицательное число)
Также устно, с полным объяснением, вычислить:
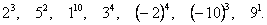
4. Изучение нового материал.
Изучить п.7, ответить на вопросы 1-5, с.61.
5. Историческая пауза.
Первыми в списке арифметических действий идут сложение, вычитание, умножение и деление. Представление о возведении в степень как о самостоятельной операции у математиков сложилось не сразу, хотя задачи на вычисление степеней встречаются в самых древних математических текстах Древнего Египта и Междуречья.
Своеобразно описывает первые натуральные степени чисел Диофант Александрийский в своей знаменитой «Арифметике»:
«Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато - квадраты — от умножения квадратов самих на себя, далее квадрато - кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо - кубы — от умножения кубов самих на себя».
6. Закрепление нового материала.
Решить № 257. 259, 262 (а, б)
7. Подведение итогов. Рефлексия.
8. Домашнее задание.
Прочитать, разобрать и выучить правила из § 7.
Решить задания № 258, 260, 262 (а, б).
Урок №6. Тема: Степень с натуральным показателем. Стандартный вид числа.
Цели урока:
изучить правило записи числа в стандартном виде и закрепить понятие степени, правила вычисления степени с натуральным показателем;
развивать у учащихся навыки вычисления степеней и решения примеров с использованием степени;
воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Ход урока:
1. Организационный момент.
2. Мотивация урока.
3.Актуализация опорных знаний. Проверка д/з.
1) Сформулируйте определение степени с натуральным показателем.
2) Каким числом является:
а) степень положительного числа
б) степень отрицательного числа с четным показателем
в) степень отрицательного числа с нечетным показателем
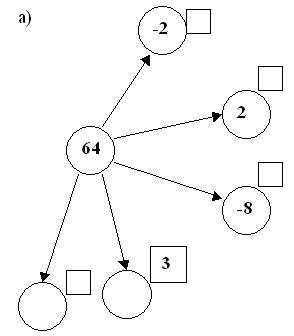
Представьте 64 в виде степени с основанием 2; -2; -8. Куб какого числа равен 64? Существует ли еще какой-нибудь способ представления 64 в виде степени с натуральным показателем? Если да, то назовите его.
б)Найдите ошибку:
3*3*3*3*3=53; (-2)2= -2*2= -4; 81 = 1; 00= 1
4. Выполнение упражнений на вычисление степеней с натуральным показателем.
Решить № 266(а- в), 267 (а, в), 268.
Изучение правила записи числа в стандартном виде.
a ∙ 10 n , где 1≤аn – натуральное число
решить №270.
Физкультурная пауза.
Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давай
Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3—4 раза.
Медленно наклоняйте голову: вперед—влево— вправо - назад. Повторите 3-4 раза.
Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.
6. Самостоятельная работа
Вариант 1: № 269 (а), 273 (а), 274 (а, б).
Вариант 2: № 269 (б), 273 (б), 275 (а, б).
7. Подведение итогов. Рефлексия.
8. Домашнее задание.
Повторить правила из § 7.
Решить задания № 266 (г, е), 267 (г), 268, 271.
Урок №7. Тема: Свойства степени с натуральным показателем.
Цели урока:
Изучить свойства степени с натуральным показателем;
развивать у учащихся навыки вычисления степеней и решения примеров с использованием свойств степени;
воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Ход урока:
1. Организационный момент.
2. Мотивация урока.
Здравствуйте ребята! Садитесь. Мы с вами продолжаем тему «Степень» и на сегодняшнем уроке познакомимся со «Свойствами степени». Урок проведем в форме деловой игры. Класс разобьем на группы, каждая группа это научно-производственное объединение, которое займется изучением свойств степени самостоятельно, используя литературу по данной теме, а затем исследует применение этих свойств.
3.Актуализация опорных знаний.
Чтобы проверить вашу готовность к усвоению новых знаний проведем устный счет.
Математический диктант.
1) Запишите в виде произведения а .
.
2) Запишите в виде степени xxx.
3) Запишите в виде степени число 8.
4) Запишите число 25 в виде степени числа 5.
5) Найдите числовое значение выражения (-11)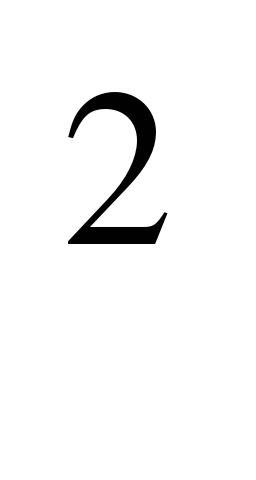 .
.
6) Найдите числовое значение квадрата числа 2/3.
7) Найдите числовое значение куба числа 0,1.
8) Может ли шестая степень какого-нибудь числа быть отрицательной?
9) Может ли пятая степень числа быть отрицательной?
10) Какое натуральное число в любой степени равно самому себе?
Вычисли устно.
0,32
(- 2)3
(- 0,2)1
62 + 82
– 92
(- 10)2∙260
– 42 + 42
4∙52
26
10) - 42 + 460
11) 52
12) 43
13) (32)2
14) (0,4 – 0,1)2
15) - 82
16) - 49 + 72
17) 0,53
Сравнить с 0:
а) (-2)³
б) (-1)²
в) -1²
г) -8²
д) 0,5³
Решить № 274 (в - е).
4. Изучение нового материал.
Каждой группе, входящей в Н.П.О. ставим одинаковую задачу: Ознакомиться с литературой по данной теме, руководителей групп или инструкторов сегодня заранее я не назначаю, по ходу урока первые в группах сдавшие мне теоретическую часть сделают опрос в своих группах остальных участников. Так как все одновременно не подготовятся к ответу я буду подходить к каждой группе поочередно. Защита теоретического материала состоится в виде заполнения пропусков на плакатах, делегата определит группа. Защиту практических навыков мы с вами проведем в виде соревнований на карточках обучающего характера и узнаем, чья же группа подготовилась лучше. Каждая группа состоит из четырех человек и получает конверт с заданием.
Сформулируйте правило умножения степеней с одинаковыми показателями
Сформулируйте правило деления степеней с одинаковыми показателями
Сформулируйте правило возведения степени в степень
Сформулируйте правило возведения в степень произведения
Сформулируйте правило возведения в степень дроби
5.Закрепление нового материала.
Отчет групп.
1012 : (24 . 54)
Представить в виде степени:
(-3)8 . (-3)4
(0,1)20 : (0,1)6
(хn)2
Найти значение выражения:
(1014 . 107) : 1019
53 . 23
Решить № 298. 300, 302, 308.
6. Самостоятельная работа
I Вариант: II Вариант:
а4 а15= а12а4=
а12:а4= а18:а9=
(а2)5= (а4)8=
(а2в3)6= (а6в4)3=
а0= в0=
7. Подведение итогов. Рефлексия.
8. Домашнее задание.
Прочитать, разобрать и выучить правила из § 8.
Решить задания № 303, 305, 309.
Урок №8. Тема: Нахождение значений выражений с использованием свойств степени с натуральным показателем.
Цели урока:
Закрепить свойства степени с натуральным показателем при нахождении значений выражений;
развивать у учащихся навыки вычисления степеней и решения примеров с использованием свойств степени;
воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Ход урока:
1. Организационный момент.
2. Мотивация урока.
«Пусть кто-нибудь попробует вычеркнуть из математики
степени, и он увидит, что без них далеко не уедешь»
М.В. Ломоносов
3.Актуализация опорных знаний. Проверка д/з.
Устная работа.
В следующих утверждениях заполните пропуски.
“При возведении в степень положительного числа получается… число”.
“При возведении в степень нуля получается …”.
“Степень отрицательного числа с четным показателем есть … число”.
“Степень отрицательного числа с … показателем есть число отрицательное”.
“Квадрат любого числа есть … число”.
“Куб … числа является положительным числом”.
“Куб … числа является отрицательным числом”.
Выполняя задания, ученик допустил ошибки. Какие свойства, правила не знает ученик?
35 . 38=340
81=1
24 + 22=26
(2а)5=2а5
(х2)3=х8
35*38=340; 52* 53=105; 24+22=26; 310:32=55
(2а)5=2а5; (х2)3 = х8; (а)3*(а2)4 = а14.
Сформулируйте правило умножения степеней с одинаковыми показателями
Сформулируйте правило деления степеней с одинаковыми показателями
Сформулируйте правило возведения степени в степень
Сформулируйте правило возведения в степень произведения
Сформулируйте правило возведения в степень дроби
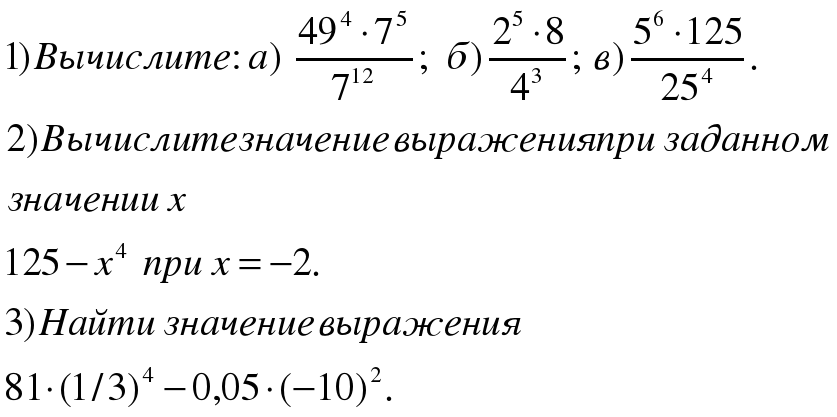
4.Нахождение значений выражений с использованием свойств степени с натуральным показателем.
Решить устно № 301, 307, письменно № 313, 319 (а- г), 322 (а, в).
Закрепить правила возведения в степень произведения и возведения в степень дроби.
Решить №311, 316 ( а- г), 325 (а, б).
5. Подведение итогов. Рефлексия.
6. Домашнее задание.
Повторить правила из § 8.
Решить задания № 310, 312, 318 (а- в), 325 (г, д).
Тема: Одночлен и его стандартный вид.
Цели:
ввести понятие одночлена, его стандартного вида, понятие коэффициента одночлена и степени одночлена; закрепить эти понятия в ходе упражнений; повторить определение и свойства степени;
развивать сообразительность, смекалку учащихся, развивать культуру их речи; развивать познавательную активность учащихся;
воспитывать целеустремленность, ответственность, организованность, формировать интерес к изучению математики
Ход урока:
1. Организационный момент.
2.Мотивация.
Назовите тему урока, разгадав ребус.

Сегодня наука алгебра поведет вас в лабораторию “Одночлены”, в которой вы узнаете, что такое одночлены, одночлены стандартного вида, коэффициент и степень одночлена.
3. Математический диктант
Ответьте письменно на следующие вопросы:
Сколько месяцев в t годах?
Сколько минут в n часах?
Сколько метров в километре?
Площадь прямоугольника со сторонами а и в равна…
Длина окружности равна…
Произведение пятой степени переменной x и четвертой степени y?
Удвоенное предыдущее выражение.
Произведение удвоенного квадрата переменной x на утроенный куб этой переменной.
Площадь квадрата со стороной c.
Любая отметка.
Записав ответы, можете проконтролировать, так как ответы для всех заданий находятся среди выражений, записанных на доске.
Все выражения перечисленные здесь, в том числе и ваши ответы, имеют общее название – одночлены или мономы.
4. Изучение нового материала.
Проанализируем строение всех этих выражений, попробуем дать определение одночлена.
Какие выражения могут быть одночленами?
Работа с учебником п.5.
Вставьте пропущенные слова в следующие определения:
Одночлен, представленный в виде произведения числового множителя, стоящего на первом месте, и степеней различных переменных называют одночленом ____________ вида.
Числовой множитель одночлена, записанного в стандартном виде, называют ________________ одночлена.
Сумму показателей степеней всех входящих в него переменной называют ____________________ одночлена.
Можете проверить себя, вставленные слова должны находиться среди следующих слов: стандартного, нулевого, дробью, коэффициентом, степенью.
5. Закрепление нового материала.
Решить устно № 88 с.45, письменно № 89, 90. 91(чет).
6. Самостоятельная работа.
№ 92. 1 вариант-нечетные, 2 вариант- четные
7. Историческая пауза.
О коэффициенте.
Термин «коэффициент», от латинского сoefficiens – содействующий (подразумевается множитель), ввёл Виет, однако в современном смысле его употребляли систематически лишь в 17 веке английские математики Оутред и Валлис, французский математик Дешаль и другие.
Коэффициентом пользовались и древнеиндийские учёные. Многие европейские математики 16- 17 веков не пользовались постоянным термином для понятия коэффициента. Так, например,
Декарт говорил об «известной величине» в члене уравнения, другой французский математик, Лопиталь (1661 – 1704), - об «умножающей величине», Ньютон писал то «предстоящее число», то «известная величина», то «член». Диофант называл коэффициент «множеством».
8. Итог урока.
Фронтальный опрос:
1) Является ли выражение 6ху одночленом?
2) Можно ли назвать одночленами -8, х, у3?
3) Что значит стандартный вид одночлена?
СИНКВЕЙ
(от англ. “путь мысли”)
Одно слово. Существительное или местоимение, обозначающие предмет, о котором идёт речь Одночлен
Два слова. Прилагательные или причастия, описывающие признаки и свойства выбранного предмета. Красивый, порядочный
Три слова. Глаголы, описывающие совершаемые предметом или объектом действия. Думай, упрощай, используй свойства степеней
Фраза из четырёх слов. Выражает личное отношение автора к предмету или объекту. Ура! Все получилось правильно!
Одно слово. Характеризует суть предмета или объекта. Произведение
Д/з: выучить п.5, решить № 94, 95 (чет).
Урок №10. Тема: Умножение одночленов. Возведение одночлена в степень.
Цели:
Выработка умений и навыков умножения одночленов, возведение одночленов в степень, применяя свойства степеней.
Развитие познавательной деятельности и активности учащихся на уроке.
воспитывать целеустремленность, ответственность, организованность, формировать интерес к изучению математики
Ход урока:
1. Организационный момент.
2.Мотивация урока.
Чтобы узнать тему урока решим анаграмму.
( Найти исходное слово).
| ОДЧЛНОЕН одночлен ЖЕНИЕУМНО умножение ПЕНЬСТЕ степень ЗАКОПАТЕЛЬ показатель |
Значит тема урока: « Умножение одночленов. Возведение одночлена в степень»
3.Актуализация опорных знаний.
1) Верно ли утверждение, определение, свойство?
Одночленом называют сумму числовых и буквенных множителей.
Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
Целое выражение, которое содержит произведение чисел и букв, называют одночленом
Сумма показателей степеней всех букв входящих в одночлен называется степенью одночлена.
Одинаковые или отличающиеся друг от друга только коэффициентами, называют подобными членами.
Алгебраическая сумма нескольких одночленов называется одночленом.
Степень одночлена не может быть равна нулю
5 это одночлен
2х2 + у3 - одночлен
Ученики осуществляют самопроверку по выведенным ответам.
Приведите одночлен к стандартному виду:
4ав2авв4а·(-5) 3а2вав4а2·(-4)
Решить устно.
Возведите в степень:
а) (ав)3; б) (а3)5; в) ( 2х3)3; г) (-4а7)2; д) (- 10х2у4)3
Вычислить:
а) (65+29)0 · (-2)3;
б) 56·52
(52)3
в) 23·16
25
4. Изучение нового материала.
«Подумай и сделай открытие»
Еще древние мудрецы считали, что «Величие человека в его способности мыслить». Нам сегодня предстоит на основании имеющихся у нас знаний получить новое знание.
- Как мы отличаем одночлен стандартного вида от одночлена нестандартного вида?
- Как привести одночлен к стандартному виду?
- Сравните выражения: (-23ав)(2а) и -46а²в
- Как их можно назвать?
- Чем они отличаются?
- Поставим цель урока. Выполнять операцию умножения одночленов через применения алгоритма приведения одночлена к стандартному виду.
- 2 а
а =(2а)
=(2а) ; 3
; 3 х
х у
у =(3ху)
=(3ху)
- назовите одночлены в правой части этих равенств.
- дайте определение одночлена.
Сравните выражения: (3ху) и 81х
и 81х у
у
- Можно ли получить второе выражение из первого?
- Какое правило можно использовать?
-Чему еще мы должны научиться? Возведению одночлена в степень.
-А удобно ли использовать формулу: а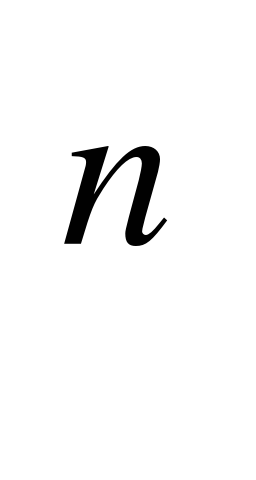 в
в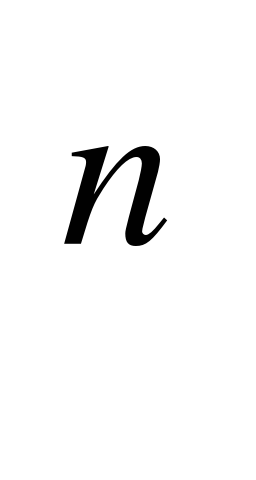 =(ав)
=(ав)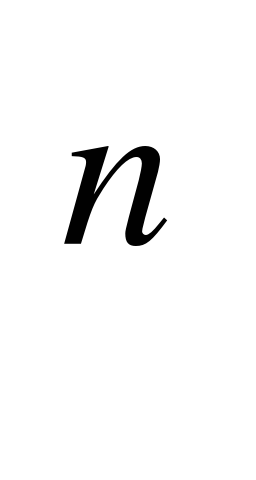 ?
?
-Как можно применить ее в новой ситуации, т.е. для возведения одночлена в степень?
Плакат с формулами вывешиваем на доске.
5. Закрепление нового материала.
А сейчас применяем данные правила при выполнении заданий.
Решить № 340, 342, 344, 352.
6. Самостоятельная работа.
Используя полученные знания, найдите верные равенства и угадайте слово. Карточки с заданиями получает каждый ученик.
5,1р q
q *(-2pq
*(-2pq )=-10,2p
)=-10,2p q С
q С
-2,5z *2zx=-5xz
*2zx=-5xz Ф
Ф
(7а²в)²=49а в² Т
в² Т
(-0,1ху )²=0,01х²у Е
)²=0,01х²у Е
(-5хус) =-125ху
=-125ху с
с Р
Р
(1/2а) =1/32а П
=1/32а П
17р²*2р 34р Ш
34р Ш
0,6х²у *2ху=1,2х
*2ху=1,2х у Е
у Е
(-10х²у )²=100х
)²=100х у Н
у Н
(1/5ec)²=1/25e²c Ь
Ответ: степень
7. Итоги урока. Д/з.
«Момент истины»
Какая была сегодня тема урока?
Какие открытия мы сделали?
Сформулируем открытые правила? Ученики дают ответы.
Решить №341, 343, 353.
Урок №11. Тема: Обобщение и систематизация знаний по теме « Степень. Одночлены».
Цели:
Обобщить и систематизировать знания учащихся по теме « Степень. Одночлены».
Развитие познавательной деятельности и активности учащихся на уроке.
воспитывать целеустремленность, ответственность, организованность, формировать интерес к изучению математики
Ход урока:
1. Организационный момент.
2.Мотивация урока.
3.Актуализация опорных знаний.
Устный опрос:
Как умножить степени с одинаковыми основаниями?
Как разделить степени с одинаковыми основаниями?
Как возвести степень в степень?
Как возвести в степень произведение? Частное?
Какие операции можно выполнять над одночленами?
При выполнении каких операций над одночленами получают одночлен, многочлен, алгебраическую дробь?
Как сложить или вычесть одночлены?
Как умножить одночлены?
Как возвести одночлен в степень?
Соедините линиями выражения, соответствующие друг другу:
| 57 53 | 53·7 | 32 35 | 32·5 |
|
| 57: 53 | 57+3 | 35: 32 | 35 · 75· |
| (2·5)7 | 23 : 53 | ( 3·7)5 | 35 : 75 |
| (57)3 | 27 · 57 | (32)5 | 32+5 |
| ()3 | 57-3 | ()5 | 35-2 |
Укажите верно выполненное сравнение степеней.
| а) (-4,8)2 3 | а) (-7.6)5 |
| б) (-6)4 | б) (-4,9)7 4 |
| в) (-3,5)4 = -3,54 | в) (-5.3)10 8 |
| г) (-8,5)3 = -8,53 | г) (-9)12 = -912 |
| д) 0 7 | д) 0 6 |
| е) (-5,1)4 (-5,1)7 | е) -1,43 = (-1,4)3 |
| Ответ: | Ответ: |
Решить устно.
Возведите в степень:
а) (а в)3; б) (а3)5; в) (2х3)3; г) (-4а7)2; д) (- 10х2у4)3
Перемножьте одночлены:
а) 3ху и 2х3у4; б) 3ху4 и х2у6
в) 4а2 и 0,5а3в г) 2,5а2в и 2а2в6
Вычислить:
а) (65+29)0 · (-2)3;
б) 56·52
(52)3
в) 23·16
25
4. Обобщение и систематизация знаний по теме « Степень. Одночлены».
Решить № 347 (а, б), 348, 354 (а, б, в, г), 356(а, б), 357.
5. Самостоятельная работа.
КВАДРАТ или КУБ?
Представьте, если возможно, в виде квадрата или куба одночлена
| 16а2 в4 | -125 с3 у9 | 1000х12у6 |
| 64 а6 в12 | -100 х4 у2 | -1х6у12 |
| -27 а3 в6 | 36 х 8у2 | 4а4в3 |
7. Итоги урока. Д/з.
Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).
Вам для этого помогут слова:
-Я узнал…
-Я почувствовал…
-Я увидел…
-Я сначала испугался, а потом…
-Я заметил, что …
-Я сейчас слушаю и думаю…
-Мне интересно следить за…
Решить №347(в, г), 349, 354(д, е), 358.
Урок № 11. Тема: Контрольная работа по теме «Степень. Одночлены».
Цели:
Проверить знания, умения и навыки учащихся по теме «Степень. Одночлены».
Развивать внимание, логическое мышление, письменную математическую речь;
Воспитывать самостоятельность, трудолюбие.
Ход урока
1.Организационный момент.
2.Мотивация урока.
3. Контрольная работа
4. Итоги урока.
Повторить п.5-9.
26

 Получите свидетельство
Получите свидетельство Вход
Вход


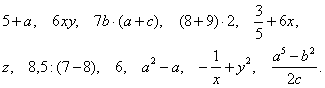

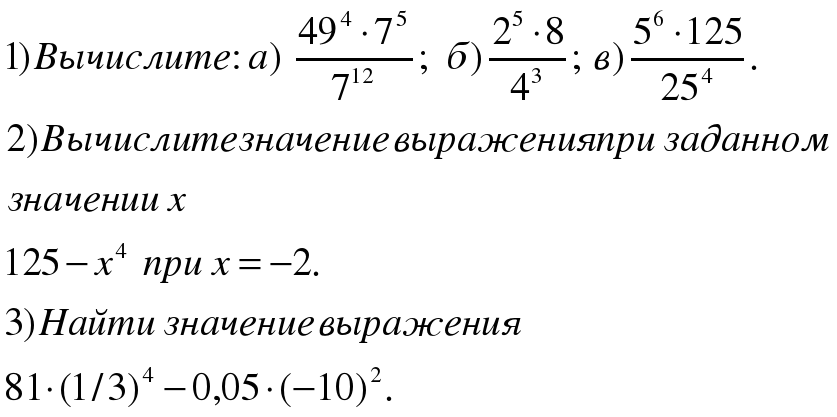










 Разработка уроков по математике по теме "Одночлены" (0.24 MB)
Разработка уроков по математике по теме "Одночлены" (0.24 MB)
 0
0 1476
1476 100
100 Нравится
0
Нравится
0


