Треугольник Паскаля

развивать сознательное использование свойств комбинаций при решении различных математических задач,

дать понятия треугольника Паскаля,

познакомить учащихся с биномом Ньютона,

формировать у учащихся комбинаторный стиль мышления, философское восприятие случайного в окружающем мире, прививать чувство прекрасного в мире математики.

Ход урока.

І.Орг. момент.

ІІ.Проверка дом. задания.

Как же решить задачу по комбинаторике?

(работа с алгоритмом: собрать его на доске с помощью готовых блоков, остальные собирают алгоритм из этих же блоков на картонке, работая в паре, затем сравнивают с доской)

Что означают символы на блоках?

С помощью какой формулы рассчитывают количество комбинаций?

Открываем тетради, записываем число, классная работа.

Решить задачу:

№1.

Сколькими способами можно разместить на полке 5 томов одного писателя так, чтобы они не были расположены один за другим в последовательности возрастания их номеров?(Р₅-1)

№2.

На плоскости выбраны 10 точек. Сколько существует треугольников с вершинами в этих точках?

№3.

Сколько различных целых трёхзначных чисел можно составить из цифр 1,2,3,4,5,6,7,8,9 так, чтобы цифры в числе не повторялись?

    ІІІ.Историческая справка.

Как сказал один из известных математиков 16 в. Стевин : «Среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью».

            Еще в Древнем Китае и Древней Греции увлекались тем, что составляли магические квадраты из чисел. В 16-17 веках, когда происходило зарождение и становление комбинаторики как науки, к этому опять обратились ученые и вот об одном из их произведений мы сегодня и поговорим. Названо оно в честь одного из авторов Блеза Паскаля (историческая справка дается учениками).

    ІV.Актуализация опорных знаний.

 Смотрите документ

       VІ.Дом.задание: Выучить теоретические сведения по конспекту, продолжить треугольник Паскаля до n=12.

       VІІ.Итог урока.

С чем мы сегодня познакомились?

Какие новые формулы получили?

Что нового узнали?

Тема урока: Решение задач. Треугольник Паскаля.

Цель и задачи урока:

• развивать сознательное использование свойств комбинаций при решении различных математических задач,

• дать понятия треугольника Паскаля,

• познакомить учащихся с биномом Ньютона,

• формировать у учащихся комбинаторный стиль мышления, философское восприятие случайного в окружающем мире, прививать чувство прекрасного в мире математики.

Ход урока.

І.Орг. момент.

ІІ.Проверка дом. задания.

• Как же решить задачу по комбинаторике?

(работа с алгоритмом: собрать его на доске с помощью готовых блоков, остальные собирают алгоритм из этих же блоков на картонке, работая в паре, затем сравнивают с доской)

• Что означают символы на блоках?

• С помощью какой формулы рассчитывают количество комбинаций?

• Открываем тетради, записываем число, классная работа.

Решить задачу:

• №1.

Сколькими способами можно разместить на полке 5 томов одного писателя так, чтобы они не были расположены один за другим в последовательности возрастания их номеров?(Р₅-1)

• №2.

На плоскости выбраны 10 точек. Сколько существует треугольников с вершинами в этих точках?()

• №3.

Сколько различных целых трёхзначных чисел можно составить из цифр 1,2,3,4,5,6,7,8,9 так, чтобы цифры в числе не повторялись?(2)

ІІІ.Историческая справка.

Как сказал один из известных математиков 16 в. Стевин : «Среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью».

Еще в Древнем Китае и Древней Греции увлекались тем, что составляли магические квадраты из чисел. В 16-17 веках, когда происходило зарождение и становление комбинаторики как науки, к этому опять обратились ученые и вот об одном из их произведений мы сегодня и поговорим. Названо оно в честь одного из авторов Блеза Паскаля (историческая справка дается учениками).

ІV.Актуализация опорных знаний.

Вычислить:

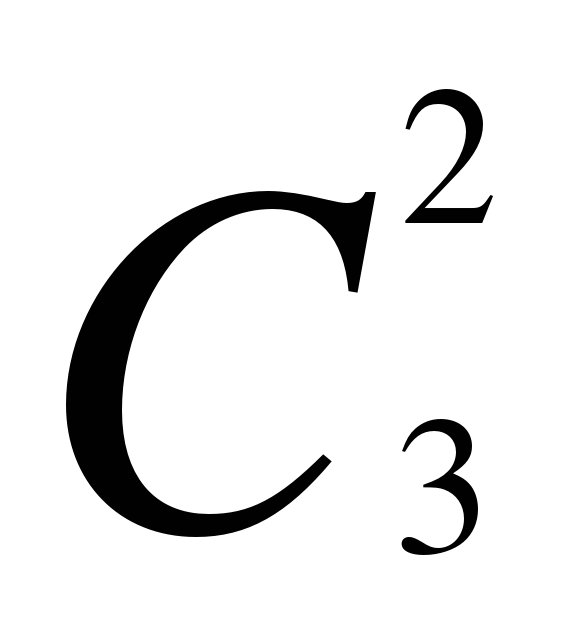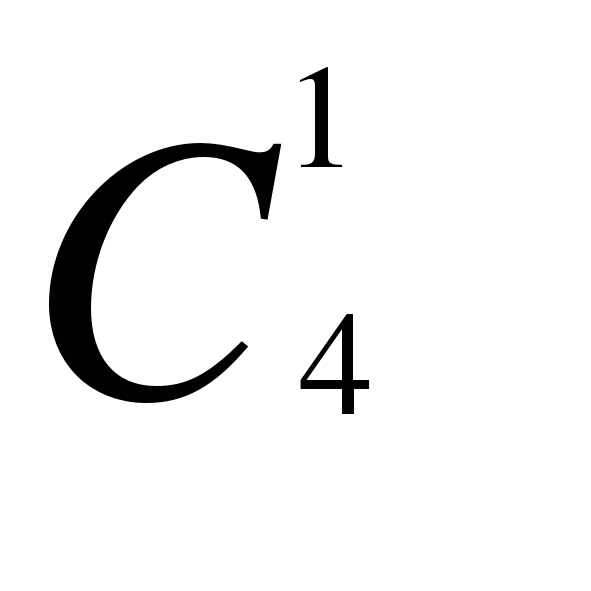и ; и ; и .

Про какую формулу-свойство нам здесь напомнили?

• =

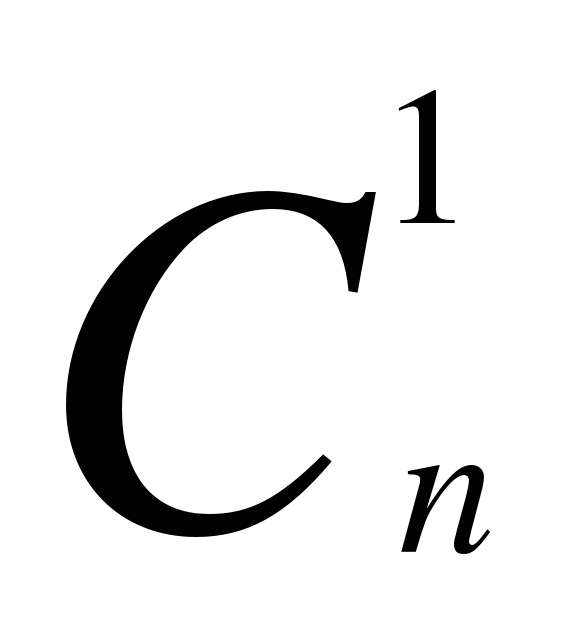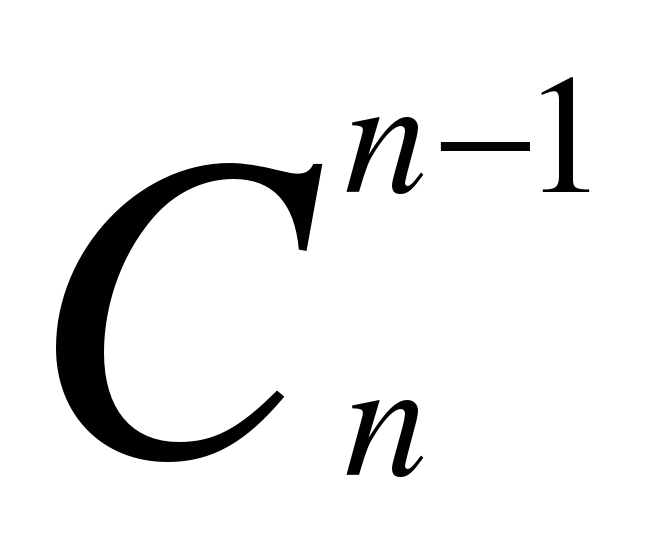
V.Новый материал (излагается в виде беседы).

Давайте сравним, например, предварительно выполнив вычисления.

и ; и ; и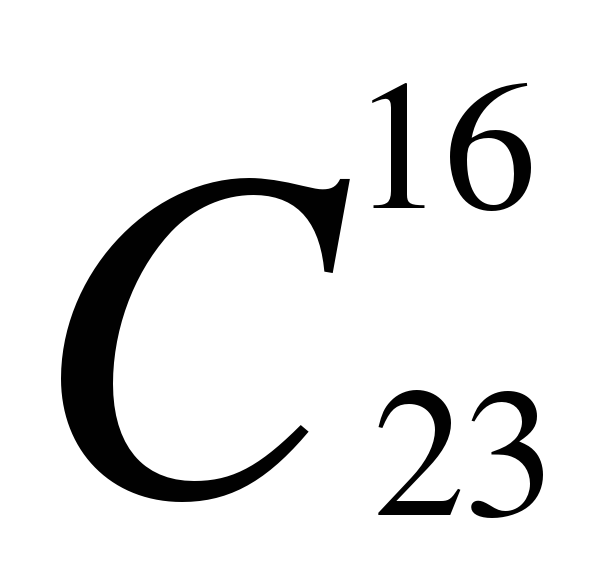

Какой вывод можно сделать?

• =

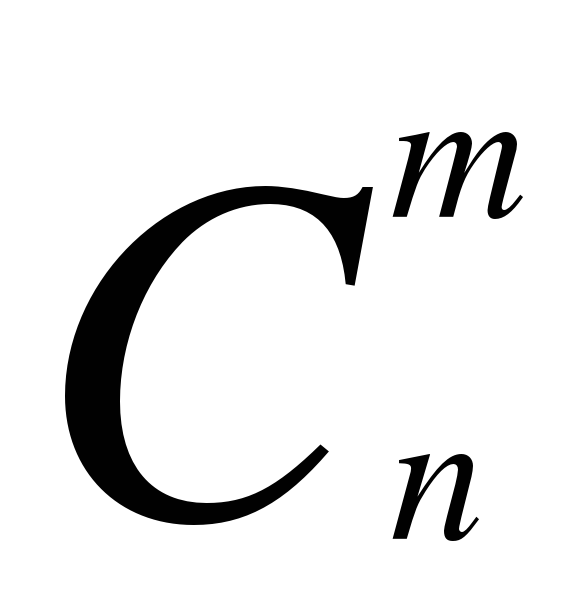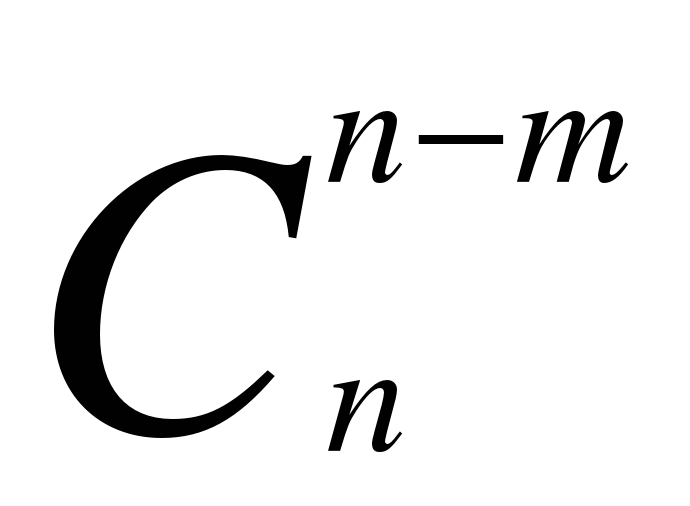
  • Если не заметили закономерности, то можно задать вопрос:

  • Что общего у С слева и справа?

  • Чем они отличаются?

  • Как связаны числа верхнего индекса?

А теперь я вам предлагаю записать это несколько иначе, вычислив устно:

n=0 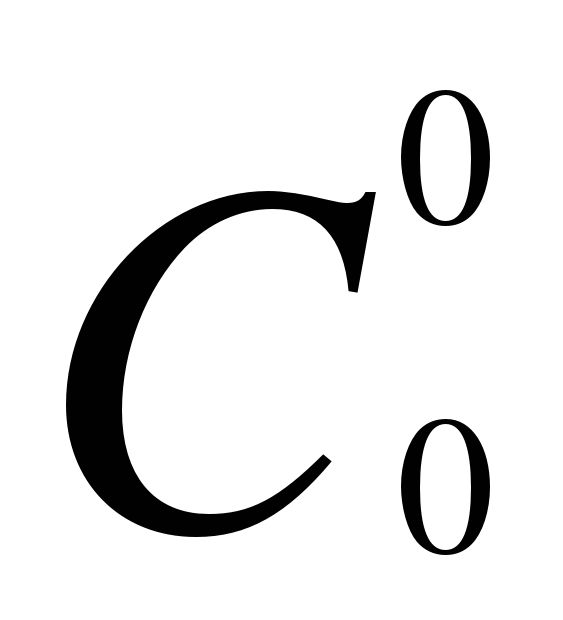1

n=1 1 1

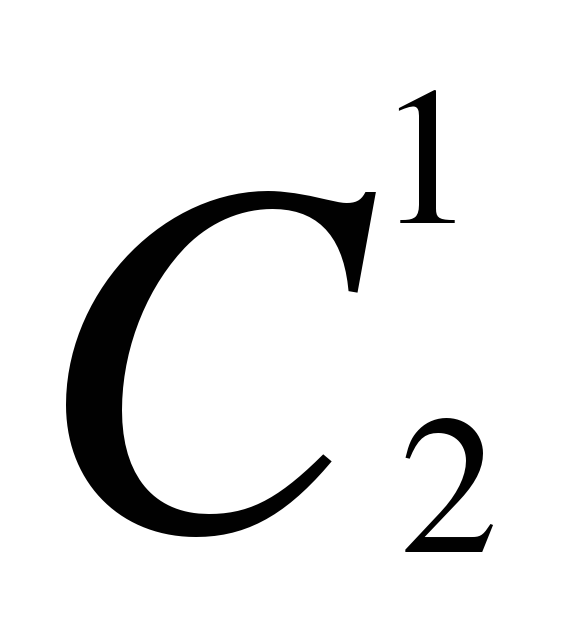
n=2 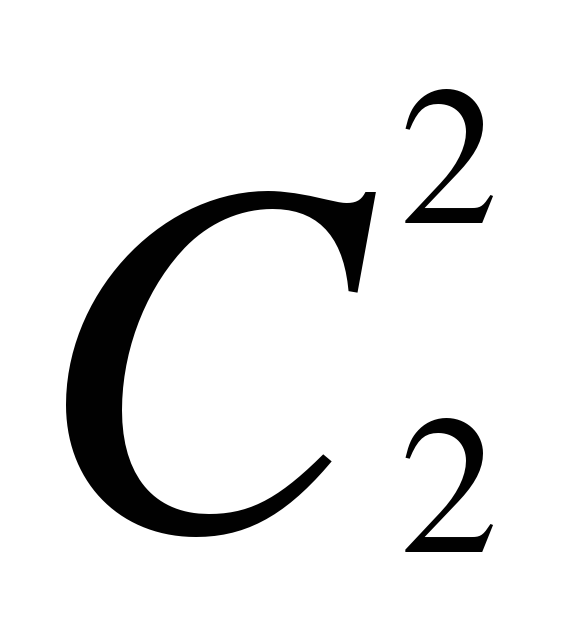1 2 1

n=3 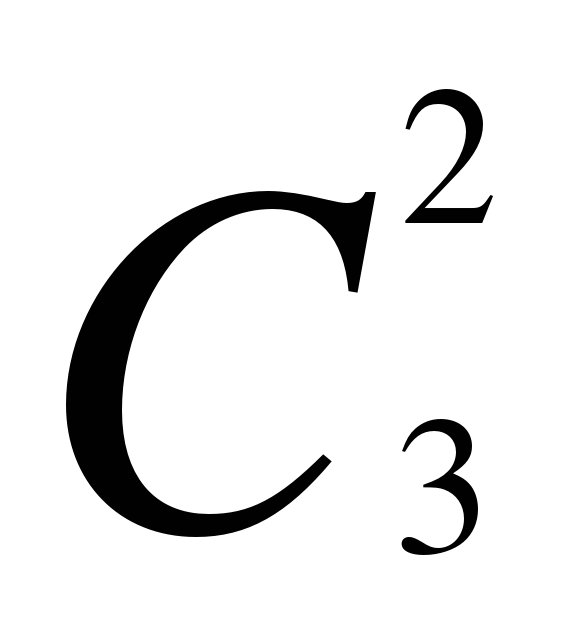1 3 3 1

На что похожа наша запись? Правильно на треугольник, который и назвали в честь Паскаля - треугольник Паскаля, так как большую известность он получим после работ этого ученого. Но частично этот треугольник был известен еще во 2 веке до нашей эры в Индии, до n=8 он приводится в трактате «Зеркало четырех элементов» китайского математика Чжу Ши-цзе 13-14 век, а в Европе до Паскаля он фигурирует в трудах Апиана (1527г.) и Штифеля (1544г.) А какая будет в нем следующая строка?

n=4 1 4 6 4 1

Записать её очень просто, заметив, что нижнее число равно сумме двух стоящих над ним чисел.

А если я предложу вам записать свойство для n-ой строки, вы сумеете записать его в общем виде?

• =+

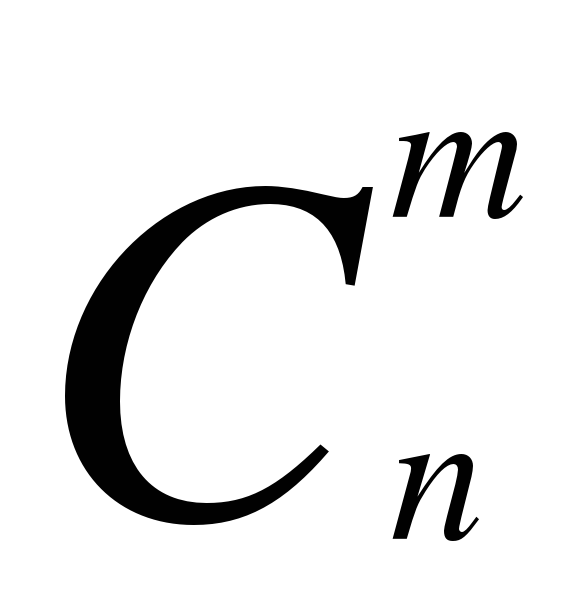А теперь обратимся на ненадолго к алгебре? Учили тему «Формулы сокращенного умножения»?

А если выписать числовые коэффициенты в них, что мы получим?

(a+b)⁰=1 1

(a+b)¹=a+b 1 1

(a+b)²=a²+2ab+b² 1 2 1

Вновь появляется треугольник Паскаля.

Проверим для n=3 (раскрываем скобки у доски). Получили

(a+b)³=a³+3a²b+3аb² +b³ 1 3 3 1

Так вот этот треугольник Паскаля помогает возвести (а+в) в любую степень, а увидел это Ньютон. Поэтому бином Ньютона – это формула сокращенного умножения для любой степени. Кстати, об этом задолго до Ньютона знал азиатский ученый и поэт Омар Хайям, еще в 12 веке. С его литературным наследием вы познакомитесь на уроках литературы, а его подробное описание бинома не сохранилось. В 1265 г. другой ученый Азии Ат-Туси написал книгу, которая дошла до наших дней где приведены формулы до n=12 включительно.

VІ.Дом.задание: Выучить теоретические сведения по конспекту, продолжить треугольник Паскаля до n=12.

VІІ.Итог урока.

С чем мы сегодня познакомились?

Какие новые формулы получили?

Что нового узнали?