МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КОМИ
КОМИ РЕСПУБЛИКАСА ЙÖЗÖС ВЕЛÖДАН МИНИСТЕРСТВО
Государственное образовательное учреждение
начального профессионального образования
профессиональное училище № 15 г. Сыктывкара
УДЖИКАСÖ ВЕЛÖДАН СЫКТЫВКАРСА 15 №-А УЧИЛИЩЕ
УЛЫС ТШУПÖДА УДЖИКАСÖ ВЕЛÖДАН ГОСУДАРТСВЕННÖЙ УЧРЕЖДЕНИЕ
Методические указания по проведению самостоятельной аудиторной и внеаудиторной работы по учебной дисциплине математика
Тема: Комбинаторика. Элементы статистики и теории вероятности
Рассмотрено методической комиссией
преподавателей естественнонаучного цикла
протокол № от « « 2013
председатель МК
Одобрено
Методист
Сыктывкар
2013
Составлено
В соответствии с требованиями Федерального государственного стандарта к минимуму содержания и уровню подготовки выпусников, утвержденного приказом Министерства образования РФ от 17.12.2010 31897
Автор: М.Г. Копецкая, преподаватель математики высшей квалификационной категории
Одобрено на заседании предметно-цикловой комиссии преподавателей естественнонаучного цикла
Рецензент:З.Ю. Елькина, заместитель директора по ТО
Редактор: М. А. Арцер. методист ГОУ НПО №15
АННОТАЦИЯ
Разработанные методические указания предназначены для обучающихся образовательных учреждений начального и среднего профессионального образования, изучающих математику на ступени основного общего образования, в частности для студентов ГОУ НПО ПУ №15 по специальностям:
190631.01 Автомеханик;
250401.07 Машинист машин по производству бумаги и картона;
150709.02 Сварщик (электросварочные и газосварочные работы);
220703.02 Слесарь по контрольно-измерительным приборам и автоматике;
140446.03 Электромонтер по ремонту и обслуживанию электрооборудования;
151013.01 машинист лесозаготовительных и трелевочных машин.
Цель методических указаний – обеспечение поддержки учебного процесса по технологиям открытого образования. Они могут применяться для различных форм обучения (аудиторной и внеаудиторной). Также пособие предназначено для обучающихся, которые не имеют возможности прослушать весь курс в полном объеме (например, по состоянию здоровья). Пособие включает в себя информационный блок, примеры решения задач, вопросы для самонтроля и задания для самостоятельного решения. Методические указания разработаны на основе технологии модульного обучения и содержит основные сведения, необходимые для организации и выполнения учебных действий обучающимися как на уроках, так и во внеаудиторное время.
Содержание пособия соответствует общедидактическим принципам организации обучения: научности, систематичности, последовательности. Наличие теоретического материала и компонентов, адресованных учащимся с различным уровнем способностей способствует формированию знаний, умений и навыков по теме «Элементы комбинаторики, математической статистики и теории вероятности»
Структурирование пособия поможет преподавателям и обучающимся преобразовать учебный процесс так, что обучающийся самостоятельно (полностью или частично) сможет обучаться по целевой индивидуализированной программе, а это создаст предпосылки не только для освоения конкретных предметных знаний и навыков в рамках отдельной дисциплины, но и для формирования совокупности “универсальных учебных действий”, обеспечивающих компетенцию “научить учиться”.
Учебное пособие может быть использовано преподавателями математики и обучающимися, которые изучают математику на базовом уровне.
Содержание:
1.Основные понятия и законы комбинаторики.
1.1 Перестановки.
1.2 Размещения.
1.3 Сочетания.
1.4 Бином Ньютона, биноминальные коэффициенты,
треугольник Паскаля.
2.Статистика.
2.1 Статистические характеристики.
2.2 Примеры решения задач.
3. Элементы теории вероятности.
3.1. Вероятность случайного события.
3.2 Примеры решения задач.
4. Вопросы для самоконтроля.
5. Задания для самостоятельного решения.
Информационный блок
Основные понятия и законы комбинаторики
Общим термином «соединения» мы будем называть три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.).
1.1Перестановки. Возьмём n различных элементов: a1 , a2 , a3 , …, an . Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается Pn . Это число равно произведению всех целых чисел от 1 до n :
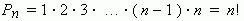
Символ n! ( называется факториал ) - сокращённая запись произведения: 1 · 2 · 3 · … · ( n – 1 ) · n .
Пример . Найти число перестановок из трёх элементов: a, b, c.
Р е ш е н и е . В соответствии с приведенной формулой: P3 = 1 · 2 · 3 = 6.
Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.
1.2 Размещения. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются размещениями из n элементов по m .
Их общее количество обозначается: 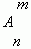 и равно произведению:
и равно произведению:
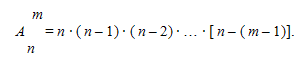
Пример. Найти число размещений из четырёх элементов a, b, c, d по два.
Решение. В соответствии с формулой получим:
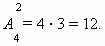
Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.
1.3 Сочетания. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, не принимая во внимание порядок расположения этих m элементов. Тогда мы получим сочетания из n элементов по m .
Их общее количество обозначается 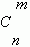 и может быть вычислено по формуле:
и может быть вычислено по формуле:
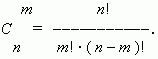
Из этой формулы ясно, что
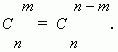
Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все n элементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1, что является определением 0! .
В соответствии с этим определением получим:
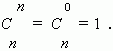
Общее число сочетаний можно вычислить, пользуясь и другим выражением:
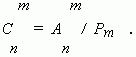
Пример. Найти число сочетаний из пяти элементов: a, b, c, d, e по три.
Решение :
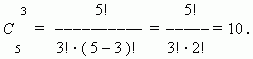
Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.
1.4 Бином Ньютона. Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:

Заметим, что сумма показателей степеней для a и b постоянна и равна n.
Пример 1.
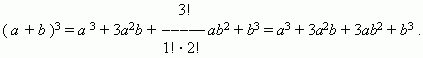
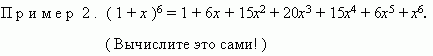
Числа 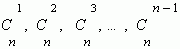 называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:
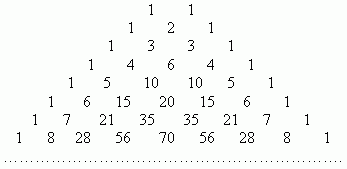
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:
( a + b )7 ,
мы можем получить результат моментально, используя таблицу:
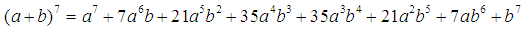
Свойства биномиальных коэффициентов.
1. Сумма коэффициентов разложения ( a + b ) n равна 2 n .
Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:
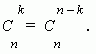
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
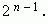
Для доказательства воспользуемся биномом: 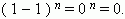 Здесь чётные члены имеют знак « + » , а нечётные - « ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна:
Здесь чётные члены имеют знак « + » , а нечётные - « ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна: 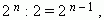 что и требовалось доказать.
что и требовалось доказать.
2.Статистика
Статистика (от лат. Status – состояние) – наука, изучающая, обрабатывающая и анализирующая количественные данные о самых разнообразных массовых явлениях в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления.
Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
Есть еще статистика финансовая, налоговая, биологическая и т.д.
Математическая статистика – наука, основанная на законах теории вероятностей. Статистические методы обработки данных из самых разных областей жизни имеют много общего. Это позволило создать универсальные научно обоснованные методы статистических исследований и проверки статистических гипотез.
2.1 Статистические характеристики – это математические понятия, с помощью которых описываются отличительные особенности и свойства совокупности данных, полученных с помощью наблюдений или каким-то другим способом. Значение характеристик состоит еще и в том, что они «подсказывают», с каких позиций целесообразно анализировать имеющуюся совокупность данных.
К статистическим характеристикам относятся: среднее арифметическое, размах, мода, медиана.
Среднее арифметическое n чисел – это частное от деления на n суммы всех этих чисел.
Размах ряда чисел – это разность между наибольшим и наименьшим числом в ряде.
Мода ряда чисел – это число, наиболее часто встречающееся в ряду.
Медианой ряда, состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить (по возрастанию или убыванию).
Медианой ряда, состоящего из четного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда, если этот ряд упорядочить (по возрастанию или убыванию).
Статистические характеристики: среднее арифметическое, мода, медиана называются средние результатов измерения
2.2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. За четверть Оля получила по геометрии пять «двоек», четыре «четверки» и две «пятерки». Ее мама считает, что за четверть Оле надо ставить «двойку», папа считает, что надо ставить «тройку», а сама Оля считает, что надо ставить «четверку». Попробуйте привести аргументы в пользу каждой точки зрения (какие статистические характеристики вычисляет каждый член семьи?). Какую бы оценку вы поставили Оле?
Решение: числовой ряд отметок Оли содержит 11 членов. Мама вычисляет моду этого ряда – отметка «2», папа – среднее арифметическое – это «3», а Оля находит медиану – это «4». При выставлении отметки за четверть прав был папа: 2 * 5 + 4 * 4 + 5 * 2 = 36/11 ~ 3,3.
Задача 2. В течение четверти Петя получил следующие отметки по математике: одну «пятерку», пять «четверок» и четыре «тройки». На сколько среднее арифметическое оценок Пети отличается от медианы этого ряда чисел?
Решение: Ряд отметок Пети по математике состоит из четного количества членов – 10 отметок. Для нахождения медианы нужно взять два элемента, стоящие посередине ряда и найти их среднее арифметическое – это получится 4. Среднее арифметическое всего ряда равно: 5 + 4 * 5 + 3 * 4 = 37/10 ~ 3,7. Значит, среднее арифметическое оценок Пети отличается от медианы ряда на 0,3.
Ответ: на 0,3.
Элементы теории вероятностей
Случайным называется событие, которое в одних и тех же условиях может произойти, а может и не произойти.
Равновозможными или равновероятными событиями называют события возможности наступления, которых одинаковы.
Маловероятные (более вероятные) события – события возможность наступления, которых мала (велика).
3.1 Вероятность случайного события
Вероятность случайного события приближенно равна частоте этого события при проведении большого числа случайных экспериментов.
Иногда вероятность выражают в процентах.
Вероятность события обозначается большой латинской буквой Р (от французского слова probabilite, что означает – возможность, вероятность).
По вероятности события можно прогнозировать частоту его появления в будущем.
Вероятностные оценки широко используют в физике и биологии, социологии и демографии, экономике и политике, спорте и т. д.
Задача 1. По статистике, на каждые 1 000 лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку?
Ответ: 0,997.
Задача 2. Какова вероятность того, что число, составленное из нечетных цифр, будет четным?
Ответ: 0.
Задача 3. Известно, что среди 1000 выпущенных лотерейных билетов 100 выигрышных. Какое наименьшее количество билетов надо купить, чтобы выиграть с вероятностью равной 1?
Ответ: 901 билет.
Задача 4. Из кошелька в темноте вынимали монетку. Известно, что-то, что вытащена, будет рублевая монета, являлось достоверным событием. Однако этот же исход при повторной попытке оказался невозможным. Сколько и каких монет было в кошельке?
Ответ: одна монета, рублевая.
Вероятностью P наступления случайного события A называется отношение  , где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:
, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: 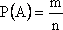 .
.
3.2 Примеры решения задач.
Пример 1. На экзамене по информатике в 9 классе – 20 билетов. Сергей не разобрался в одном билете и очень боится его вытянуть. Какова вероятность, что Сергею достанется несчастливый билет?
Решение: Всего у данного эксперимента «вытянуть наугад один билет» 20 исходов, все они равновероятны. У Сергея только один шанс из 20 вытянуть несчастливый билет. Поэтому вероятность того, что ему достанется несчастливый билет, равна 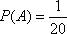 .
.
Ответ: 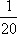 .
.
Пример 2. В лотерее 10 выигрышных билетов и 240 билетов без выигрыша. Какова вероятность выиграть в эту лотерею, купив один билет?
Решение: В лотерее разыгрывается всего 240 + 10 = 250 билетов, любой из них можно купить с одинаково вероятностью. Есть 10 шансов из 250 выиграть, и, следовательно, вероятность выигрыша равна  .
.
Ответ:  .
.
Задача 3. В вазочке перемешаны 15 конфет «Чародейка» и 5 конфет «Белочка». Когда из-за аварии погас свет, Маша наугад схватила одну конфету. Какова вероятность, что ей досталась «Белочка»?
Ответ:  .
.
Задача 4. Наудачу выбрано двузначное число. Какова вероятность того, что оно окажется:
1) четным;
2) меньшим 12?
Ответ: 1)  ; 2)
; 2)  .
.
Задача 5. В классе 30 человек. Вероятность того, что при случайном выборе одного ученика по номеру в журнале выбранным окажется мальчик, равна  . Сколько в этом классе девочек?
. Сколько в этом классе девочек?
Ответ: 20 девочек.
Задача 6. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение:
Возможен такой вариант решения.
Какие возможны исходы двух бросаний монеты?
1) Решка, решка.
2) Решка, орел.
3) Орел, решка.
4) Орел, орел.
Это все возможные события, других нет. Нас интересует вероятность 2-го или 3-го события.
Всего возможных исходов 4.
Благоприятных иcходов – 2.
Отношение 2/4 = 0,5.
Достоверные события – события, которые в обычных условиях происходят всегда, обязательно.
Невозможные события – события, которые в данных условиях никогда не происходят.
Достоверные и невозможные события встречаются в жизни сравнительно редко, можно сказать, что мы живем в мире случайных событий.
Теория вероятностей – это наука, которая изучает закономерности наступления случайных событий, что позволяет оценить шансы наступления случайного события.
Возможность наступления случайного события зависит от условий, в которых оно рассматривается.
Умение оценивать вероятность наступления события очень полезно при принятии обоснованного решения, на пример стоит участвовать в лотерее или игре.
Вопросы для самоконтроля
Перечислите основные понятия комбинаторики.
Что такое перестановки ?
Дайте определение понятию размещения
Что такое сочетание?
Какова формула для числа сочетаний?
Как строится треугольник Паскаля?
Перечислите свойства биноминальных коэффициентов.
Назовите статистические характеристики
Что называется вероятностью события?
Приведите примеры событий, вероятность которых равна 1,  ;
;  ;
;  ; 0.
; 0.
5. Задачи для самостоятельного решения.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа  так, чтобы числа
так, чтобы числа  стояли рядом и притом шли в порядке возрастания?
стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 5, 7, 8, если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа 4:
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы  и
и  оказались рядом?
оказались рядом?
16.  девочек и
девочек и  мальчиков рассаживаются произвольным образом в ряду из
мальчиков рассаживаются произвольным образом в ряду из  мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17.  девочек и
девочек и  мальчиков рассаживаются произвольным образом в ряду из
мальчиков рассаживаются произвольным образом в ряду из  мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
18.Определите моду, среднее арифметическое и размах ряда: 5, 6, 11, 11, – 1.
19.Группу детского сада (20 человек) ведут на прогулку. Сколько существует способов поставить детей в пары в колонне?
20.Костя сдает экзамен по биологии. Ему нужно выучить 21 билет. Он знает 11 билетов, а два только прочитал. Какова вероятность того, что на экзамене он вытащит билет, который даже не читал?
21 .Определите моду, среднее арифметическое и размах ряда:15, 4, 12, – 3, 15.
22. В отряде 25 бойцов. Двоих надо отправить в разведку. Сколько существует вариантов это сделать?
23. Наташа выучила 12 билетов по информатике из 20. На три билета у неё нет ответов. Какова вероятность, что на экзамене по информатике ей попадется билет, которого она не знает?
24. В чемпионате по гимнастике участвуют 50 спортсменок: 15 из Норвегии, 18 из Дании, остальные — из Швеции. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Швеции.
25. Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится четыре сумки со скрытыми дефектами. Найдите вероятность того что купленная сумка окажется качественной. Результат округлите до сотых.
26. Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 20 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
27. В сборнике билетов по физике всего 40 билетов, в 8 из них встречается вопрос по электростатике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по электростатике.
28. На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 5 прыгунов из Швеции и 3 прыгуна из Мексики. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что сорок четвертым будет выступать прыгун из Мексики.
29.
Научная конференция проводится в 3 дня. Всего запланировано 75 докладов — в первый день 27 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? 30.На семинар приехали 4 ученых из Швеции, 4 из России и 2 из Италии. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что четвертым окажется доклад ученого из Швеции.
31. В соревнованиях по толканию ядра участвуют 3 спортсмена из Японии, 9 спортсменов из Кореи, 7 спортсменов из Китая и 6 — из Индии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Индии.
32. На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 4 прыгуна из Италии и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что девятым будет выступать прыгун из Парагвая.
33. Конкурс исполнителей проводится в 5 дней. Всего заявлено 60 выступлений — по одному от каждой страны. В первый день 24 выступления, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
34. В сборнике билетов по философии всего 20 билетов, в 19 из них встречается вопрос по Пифагору. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по Пифагору
35. На семинар приехали 5 ученых из Австрии, 4 из Германии и 6 из Сербии. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что десятым окажется доклад ученого из Сербии.
36. Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 27 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
37. В среднем из 2000 садовых насосов, поступивших в продажу, 14 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
38. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 3 очка. Результат округлите до сотых.
39. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.
40. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
41. Катя дважды бросает игральный кубик. В сумме у нее выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.
42. Лена четырежды бросает игральный кубик. В сумме у неё выпало 7 очков. Найдите вероятность того, что при втором броске выпало 4 очка.
43. Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при одном из бросков выпало 2 очка.
44. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что три раза выпадет решка.
45. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
46. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз.
47. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет ровно один раз.
48. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
49. В кармане лежат 10 ключей, из которых к данному замку подходит лишь один, но неизвестно, какой. Из кармана извлекаются ключи случайным образом один за другим, и делается попытка открыть замок. Найти вероятность того, что замок будет открыт с 7-й попытки.
50. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.

 Получите свидетельство
Получите свидетельство Вход
Вход



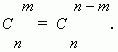
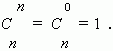
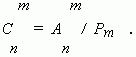
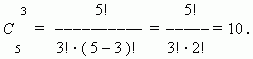

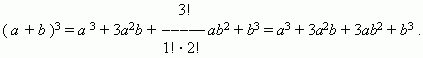
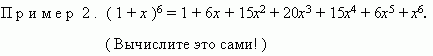
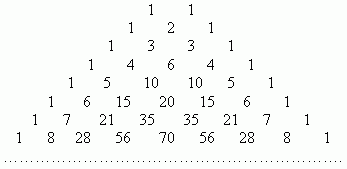
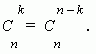









 Методические указания по самостоятельной работе по математике по теме "Комбинаторика. Элементы статистики и теории вероятности" (68.83 КB)
Методические указания по самостоятельной работе по математике по теме "Комбинаторика. Элементы статистики и теории вероятности" (68.83 КB)
 0
0 1204
1204 86
86 Нравится
0
Нравится
0


