В нашей системе образования математика до недавнего времени занимала приоритетную роль. Интерес к этой дисциплине был высок. В последнее время в связи с профилизацией школ наблюдается усиление интереса к гуманитарным дисциплинам: история, общество и т. д. Появилось значительно число профильных гуманитарных школ и классов. Характерными особенностями таких школ и классов является: увеличение числа часов, отводимых на изучение дисциплин гуманитарного цикла; сокращение времени на изучение естественно - математических предметов.
Как показывает мой педагогический опыт основной проблемой работы в классах с гуманитарным профилем – это преподавания учебного предмета на профильном уровне, т. е отбор содержания и обеспеченность учебной литературой. При преподавании математики в классах гуманитарного профиля у учащихся возникают проблемы «Что учить? Как учить?». С 2005 года на всей территории РФ вводится экзамен по математике за курс средней школы в форме ЕГЭ, в том числе в школах Республики Тыва. Наряду с другими профилями учащиеся гуманитарных классов должны овладеть знаниями, умениями и навыками, достаточными для сдачи ЕГЭ. Поэтому в настоящее время перед учителем ставится сложная задача в преподавании математики в гуманитарных классах.
Вопрос об особенностях познавательной деятельности учащихся в классах гуманитарного профиля на сегодняшний день мало разработан. Можно указать лишь на исследования В. А. Крутецкого, С. И. Шапиро, Н. А. Берулава, касающихся учеников гуманитарных классов. Исследования психологов указывают на некоторые особенности у детей - гуманитариев. Они строят свои рассуждения развернуто, наблюдается очень слабая связь между прямыми и обратными понятиями [2, c. 10].
В процессе изучения математического содержания они прежде всего запоминают конкретную формулу, учат почти наизусть доказательства теоремы. Они забывают, то затрудняются при восстановлении доказательства.
При решении задач они обращают внимание на соответствие условия задачи реальной действительности. Первоначальное осмысление задачи проходит именно здесь, а затем только они переводят ее на математический язык. У них вызывают интерес исторические сведения и факты. В процессе преподавания математики в классах гуманитарного профиля необходимо учесть эти особенности. Важным этапом для формирования интереса к математике у учащихся гуманитарного профиля является предпрофильная подготовка, одним из направлений которой могут быть спецкурсы. Они направлены на то, чтобы развить интерес школьников к предмету, познакомить их с новыми идеями и методами, расширить представления об изучаемом в основном материале, прорешать интересные задачи. Материал подбирается таким образом, чтобы можно было проиллюстрировать применение математики на практике, показать связь математики с другими областями знаний [3, с. 12].
Мной были разработаны и апробированы в школе методические материалы для предпрофильной подготовки, которые включали следующие разделы:
- Процентные вычисления и пропорции в жизненных ситуациях
- Функции и графики вокруг нас
- Золотое сечение
- Вариации на тему «Сказки про аксиомы геометрии»
- Треугольник Паскаля
Остановлюсь на некоторых примерах из этих разделов.
Пример 1. Калорийность шоколадных конфеток относится к калорийности вареного мяса как 5:1, а калорийность вишни, как 25:1. Каков будет вес мяса или вишни, эквивалентный по калорийности 3 шоколада по 100 граммов каждая?
Ответ: 1, 5 мяса, 7, 5 кг вишни.
Пример 2. Минимальный необходимый 12 - летнему школьнику объем молочных продуктов относится ко всему выпиваемому за день объему жидкости, как 3:20. Сколько молока, кефир а или жидкости должен выпивать шестиклассник, если всего в день в его рацион входит 2 литра жидкости?
Ответ: 300 г.
Учитывая интенсивную скорость роста в этом возрасте, надо помнить, что потребность в жидкости очень высока. Дефицит кальция ведет к нарушению формирования костей и зубов, задержке роста. Молоко можно кефиром, кефир - йогуртом.
Пример 3. Из 550 учащихся школы в референдуме по вопросу о введении Ученического совета участвовали 88% учащихся. На вопрос референдума 75% принявших участие в голосовании ответили «да». Какой процент от числа всех учащихся школы составили те, кто ответил положительно?
Решение: Выразим проценты дробями и вычислим число учащихся, утвердительно ответивших вопрос референдума: 550*0, 88*0, 75=363 (чел. ). Теперь найдем ответ на вопрос задачи: 363:550=0, 66 - это 66%.
Основная цель таких задач – показать широту применения в жизни такого простого и известного учащимся математического аппарата, как процентные вычисления и пропорции.
Функциональная линия является одной из основных в школьном курсе математики, пропедевтика которой начинается еще в начальной школе.
Ученики с удовольствием решают задачи на построение графиков функций, в результате которого получаются различные рисунки «Зайчик», «Лебедь», «Зонтик» и другие.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



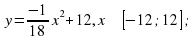
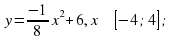
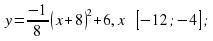
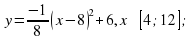
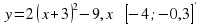
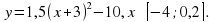










 Некоторые особенности преподавания математики в гуманитарных классах (29.84 КB)
Некоторые особенности преподавания математики в гуманитарных классах (29.84 КB)
 0
0 942
942 90
90 Нравится
0
Нравится
0


