Тестовые задания

Вариант № 1

1.  Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.

2. Площадь пря­мо­уголь­но­го тре­уголь­ни­ка равна  Один из ост­рых углов равен 60°. Най­ди­те длину катета, ле­жа­ще­го на­про­тив этого угла.

3. 

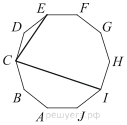ABCDEFGHIJ — правильный десятиугольник. Найдите угол ECI. Ответ дайте в градусах.

4. Основания тра­пе­ции равны 4 см и 10 см. Диа­го­наль трапеции делит сред­нюю линию на два отрезка. Най­ди­те длину боль­ше­го из них.

5. 

Найдите больший угол равнобедренной трапеции , если диагональ  образует с основанием  и боковой стороной  углы, равные 36° и 19° соответственно. Ответ дайте в градусах.

6. 

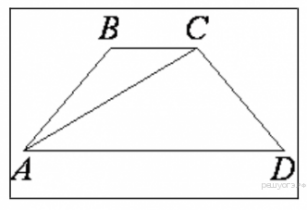
Основания рав­но­бед­рен­ной тра­пе­ции равны 4 и 14, бо­ко­вая сто­ро­на равна 13. Най­ди­те длину диа­го­на­ли трапеции.

7. 

Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

8. 

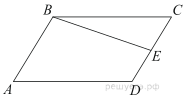
Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 120. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции ABED.

9. 

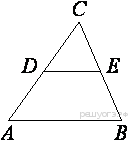В тре­уголь­ни­ке ABC известно, что DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 76. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

10. Основания тра­пе­ции равны 7 и 63, одна из бо­ко­вых сторон равна 18, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те площадь трапеции.

11. Один из углов равнобедренной трапеции равен 113°. Найдите меньший угол этой трапеции. Ответ дайте 
в градусах.

12. Какие из следующих утверждений верны?

1) Сумма углов выпуклого четырехугольника равна 180°.

2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

3) Диагонали квадрата делят его углы пополам.

4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

Если утверждений несколько, запишите их номера в порядке возрастания.

13 Какие из следующих утверждений верны?

1) Каждая сторона треугольника меньше разности двух других сторон.

2) В равнобедренном треугольнике имеется не более двух равных углов.

3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.

4) В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.

14. Какие из данных утверждений верны? Запишите их номера.

1) Вокруг любого треугольника можно описать окружность.

2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180° , то эти прямые параллельны.

3) Площадь треугольника не превышает произведения двух его сторон.

15. Какие из следующих утверждений верны?

1. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2. В тупоугольном треугольнике все углы тупые.

3. Любой квадрат является прямоугольником.

Вариант № 2

1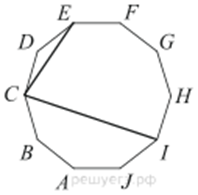 ABCDEFGHIJ — правильный десятиугольник. Найдите угол ECI. Ответ дайте в градусах.

2. 

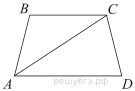В трапеции  известно, что ,  и . Найдите угол . Ответ дайте в градусах.

3. В па­рал­ле­ло­грамм впи­са­на окруж­ность. Най­ди­те пе­ри­метр па­рал­ле­ло­грам­ма, если одна из его сто­рон равна 6.

4. 

В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.

5. Пло­щадь ромба равна 27, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.

6. 

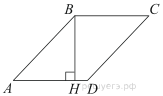Высота  ромба  делит его сторону  на отрезки  и . Найдите площадь ромба.

7. 

В трапеции ABCD известно, что AD=4, BC=2, а её площадь равна 69. Найдите площадь треугольника ABC.

8. В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, а угол, ле­жа­щий напротив основания, равен 120°. Най­ди­те площадь треугольника, делённую на 

9. Площадь прямоугольного треугольника равна  Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.

10. 

В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC соответственно. Пло­щадь тре­уголь­ни­ка CNM равна 94. Най­ди­те пло­щадь четырёхугольника ABMN.

11. Один из углов прямоугольной трапеции равен 82°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

12. Укажите номера верных утверждений.

1) Если угол острый, то смежный с ним угол также является острым.

2) Диагонали квадрата взаимно перпендикулярны.

3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

13Какое из следующих утверждений верно?

1) Сумма острых углов прямоугольного треугольника равна 90 градусам.

2) Средняя линия трапеции равна сумме её оснований.

3) В любой четырёхугольник можно вписать окружность.

14Какие из данных утверждений верны? Запишите их номера.

1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) У равностороннего треугольника есть центр симметрии.

15 Какое из следующих утверждений верно?

1. Площадь квадрата равна произведению двух его смежных сторон.

2. Диагональ трапеции делит её на два равных треугольника.

3. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

В ответ запишите номер выбранного утверждения.

Вариант № 3

1. 

В треугольнике два угла равны 57° и 86°. Найдите его третий угол. Ответ дайте в градусах.

2. 

Четырёхугольник  вписан в окружность. Угол  равен 51°, угол  равен 42°. Найдите угол . Ответ дайте в градусах.

3. Диагональ BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 65° и 50°. Най­ди­те мень­ший угол параллелограмма.

4. 

Прямые m и n параллельны. Найдите ∠3, если ∠1 = 22°, ∠2 = 138°. Ответ дайте в градусах.

5. Найдите мень­ший угол рав­но­бед­рен­ной трапеции, если два ее угла от­но­сят­ся как 1:2. Ответ дайте в градусах.

6. 

Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 216, а бо­ко­вая сто­ро­на — 78. Най­ди­те пло­щадь тре­уголь­ни­ка.

7. 

В тре­уголь­ни­ке ABC известно, что DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 35. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

8.

Сторона рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на .

9. Основания тра­пе­ции равны 4 и 14, одна из бо­ко­вых сторон равна , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те площадь трапеции.

10. 

В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, основание — , а угол, ле­жа­щий напротив основания, равен 120°. Най­ди­те площадь треугольника, деленную на 

11. Один из углов прямоугольной трапеции равен 64°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

12. Укажите номера верных утверждений.

1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

12.Какое из следующих утверждений верно?

1) Внешний угол треугольника равен сумме его внутренних углов.

2) Диагонали ромба точкой пересечения делятся пополам.

3) Касательная к окружности параллельна радиусу, проведённому в точку касания.

13.Какое из следующих утверждений верно?

1) Точка пересечения двух окружностей равноудалена от центров этих окружностей.

2) В параллелограмме есть два равных угла.

3) Площадь прямоугольного треугольника равна произведению длин его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

14.Какие из данных утверждений верны? Запишите их номера.

1) Площадь квадрата равна произведению его диагоналей.

2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Вокруг любого параллелограмма можно описать окружность.

15. Какое из следующих утверждений верно?

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Диагонали ромба равны.

3) Тангенс любого острого угла меньше единицы.

.

Вариант № 4

1.  В выпуклом четырёхугольнике  известно, что , , , . Найдите угол . Ответ дайте в градусах.

2.  Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен   Най­ди­те её боль­шее основание, если мень­шее ос­но­ва­ние равно вы­со­те и равно 8.

3.  Найдите величину острого угла параллелограмма , если биссектриса угла  образует со стороной  угол, равный 31°. Ответ дайте в градусах.

4.  Тангенс острого угла прямоугольной трапеции равен . Найдите её большее основание, если меньшее основание равно высоте и равно 14.

5.  Найдите больший угол равнобедренной трапеции , если диагональ  образует с основанием  и боковой стороной углы, равные 11° и 63° соответственно. Ответ дайте в градусах.

6. 

Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

7.  Площадь прямоугольного треугольника равна  Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.

8.  В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, основание — , а угол, ле­жа­щий напротив основания, равен 120°. Най­ди­те площадь треугольника, деленную на 

9. Основания тра­пе­ции равны 9 и 54, одна из бо­ко­вых сторон равна 27, а си­нус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те площадь трапеции.

10. Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

11. Один из углов прямоугольной трапеции равен 51°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

12Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Если утверждений несколько, запишите их номера в порядке возрастания.

13. Какие из следующих утверждений верны?

1) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.

2) Площадь трапеции равна произведению суммы оснований на высоту.

3) Площадь трапеции не превосходит произведения средней линии на высоту.

4) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.

14Укажите номера верных утверждений.

1) Если угол острый, то смежный с ним угол также является острым.

2) Диагонали квадрата взаимно перпендикулярны.

3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

15. Укажите номера верных утверждений.

1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.