Получите свидетельство
Вход
Вариант 1
1. Жизненная ёмкость лёгких – это:
А) максимальный объём воздуха, вентилируемый в течение 1 минуты
Б) объём воздух, остающегося в лёгких после спокойного выдоха
В) максимальный объём воздуха, который можно вдохнуть после спокойного выдоха
2. Величина резервного объёма выдоха у взрослого человека составляет:
А) 1,2 – 1,4 л
Б) 1,2 – 1,5 л
В) 1,3 – 1,6 л
3. По какой формуле нужно рассчитывать количество молока, необходимое ребёнку в сутки, если его масса больше 3200гр?
А) МП = n . 80
Б) МП = n . 70
В) МП = n . 100
4. Суточная калорийность пищевого рациона ребёнка определяется по формуле:
А) Q = 100+100 . n
Б) Q = 1000+150 . n
В) Q = 1000+100 . n
5. Минутный объём кровообращения равен:
А) 4-8 л/мин
Б) 6-4 л/мин
В) 4-6 л/мин
Г) 8-4 л/мин
6. Пульсовое давление равно:
А) СД+ДД
Б) СД-ДД
В) СД . ДД
Г) ДД-СД
7. Сколько пределов может иметь одна функция?
А) 2
Б) зависит от самой функции
В) 1
8. Чему равен предел суммы конечного числа, если существуют конечные пределы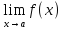 
и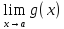 
А)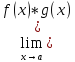 
Б) 0
В)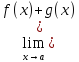 
11. Каким способом нельзя задать числовую последовательность?
А) изображение
Б) числовой
В) аналитический
Г) реккурентный
12. Найдите х3, если х1 = 1, формула хn+1 = ( n + 1 ) xn , х3 = :
А) 6
Б) 3
В) 1
Г) 0
13. Найдите х3, если хn =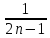 
, n Є N, x3 = :
А) 1
Б)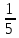 
В)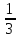 
Г) 2
14. Критические точки – это внутренние точки области определения, в которой…
А) F’(x) = 0 и существует
Б) F’(x) ≠ 1 и существует
В) F’(x) = 0 или не существует
Г) F’(x) = 1 и не существует
15. Найдите наибольшее значение функции у = 2х2 на [ 0; 2 ]
А) 2
Б) 0
В) 4
Г) 8
16. Если F’(x) 0 на каком-то промежутке, то функция на этом интервале..
А) убывает
Б) прерывается
В) возрастает
Г) не существует
17. Разность f(x0 + ∆x) – f(x0) функции f в точке х0 называется:
А) приращением аргумента
Б) приращением функции
В) производной функции
18. Приращение показывает изменение ординаты и абсциссы:
А) прямой
Б) касательной
В) точки
19. Найти приращение аргумента ∆х и приращение функции ∆f в точке х0, если f(x) = x2,
Х0 = 2; х = 1.9
А) 0,39
Б) – 0,39
В) 39
20. Исследовать функцию у = х3 на монотонность на всей числовой прямой
А) функция убывает
Б) функция возрастает
В) функция прерывается
Ответы:
В
А
А
В
В
Б
Б
Б
А
Б
Б
А
Б
В
Г
В
Б
Вариант 2
1.Точки минимума и максимума называются точками…
А) экстремума
Б) производной
В) предела функции
2. Точку х0 называют точкой… функции у = f(x), если для всех х из её окрестности справедливо неравенство f(x0)≥f(x)
А) нечётности
Б) минимума
В) максимума
3. Какой вид будет иметь уравнение касательной к графику функции у = х2-3 в точке с абсциссой х0=1?
А) у = х+3
Б) у = 2х+4
В)у = х-2
Г) у = 2х-4
4. При нахождении f′(x0) мы находим:
А) значение самой функции
Б) значение производной в точке х0
В) значение производной в точке х
Г) значение f(x0)
5. Равенство, которое выполняется для первообразной
А) F′(x) = F(x)
Б) F(x) = f′(x)
В) F′(x) = f(x)
6. Основное свойство первообразной:
А) любая первообразная для f(x) на промежутке i может быть записана в виде F(x)+C
Б) любая первообразная для f(x) на промежутке i может быть записана в виде F(x) – C+1
В) любая первообразная для f(x) на промежутке i может быть записана в виде F(x) + C-1
7. Функция ⅟х, х 0 является первообразной
А) 2х + С
Б) Inx + C
В) –Inx + C
8. Что называют монотонностью функции?
А) функция, меняющаяся в одном и том же направлении
Б) функция имеет точку разрыва
В) функция обращается в ноль
9. Линейная функция y=kx + m будет возрастать, если
А) k0
Б) k
В) k=0
10. Если функция y=g(x) возрастает на любом отрезке, а функция y=f(x) убывает, то уравнение f(x)=g(x) имеет
А) не более двух корней
Б) не более одного корня
В) не меньше трёх корней
11. Ребёнок от 6 недель до 4 месяцев должен получать молоко в размере:
А) ⅛ массы своего тела
Б) ⅙ массы своего тела
В) ⅕ массы своего тела
12. Формула для детей старше 2-х месяцев:
А) 800 + 50*(n-2)
Б) 800+ 50*(n+2)
В) 800 +50*n
13. Жизненный объём лёгких у мужчин составляет:
А) 3,4-4,5л
Б) 3,0 – 4,0л
В) 3,5 – 5,0л
14. Дыхательным альвеолярным объёмом называется:
А) объём воздуха, который проходит через лёгкие за 1 минуту во время максимальных по частоте и глубине движений
Б) часть дыхательного объёма, которая участвует в газообмене с лёгочной кровью
В) максимальный объём воздуха, который способен вдохнуть человек после спокойного вдоха
15. Разность f(x+∆x) – f(x0) функции f в точке х0 называется:
А) приращением аргумента
Б) приращением функции
В) производной функции
16. Для наименьшего значения функции y=F(x) справедливо неравенство
А) F(x) F(x0)
Б) F(x) ≥ F(x0)
В) F(x) ≤ F(x0)
Г) F(x) = F(x0)
17. Найдите наибольшее значение функции у=х на [ 1; 2]
А) 2
Б) 1
В) 0
Г) -1
18. Чему равен предел lim x/x+1 (при х→∞)
А) 0
Б) 1
В) 2
19. Какой формулой определяется длина дуги кривой?
А) L= интеграл корень 1+(f (x) )^2dx
Б) V= интеграл S(x)dx
20. Когда определённый интеграл меняет знак на противоположный?
А) при перестановке пределов интегрирования
Б) при постоянном множестве
В) если существуют интегралы для любых чисел а, в, с
Ответы:
А
В
Г
Б
В
А
Б
А
А
Б
Б
А
В
Б
Б
Б
А
В
А
А
Тест по математике (23.73 KB)
0
92
0
Нравится
0
