Получите свидетельство
Вход
Параллельность прямых и плоскостей
Вариант I
Две прямые в пространстве называются параллельными, если они не пересекаются.
Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в этой плоскости.
Если средняя линия трапеции лежит в плоскости
, то основания трапеции пересекают эту плоскость.Если прямая
параллельна линии пересечения плоскостей и 
, то прямая 
параллельна плоскости .Прямая и плоскость называются параллельными, если они не имеют общих точек.
Через данную точку пространства можно провести только одну прямую, параллельную данной плоскости.
Если стороны АВ и ВС параллелограмма
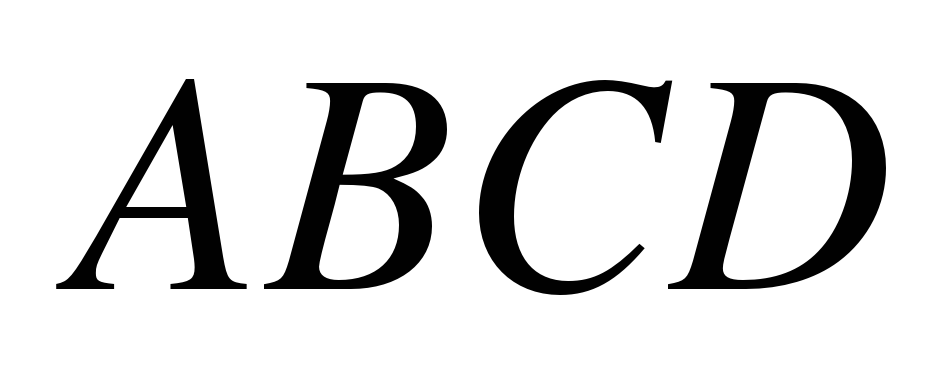пересекают некоторую плоскость, то прямые 
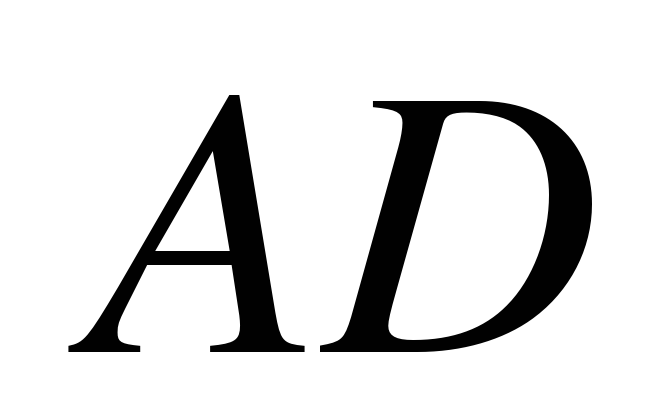и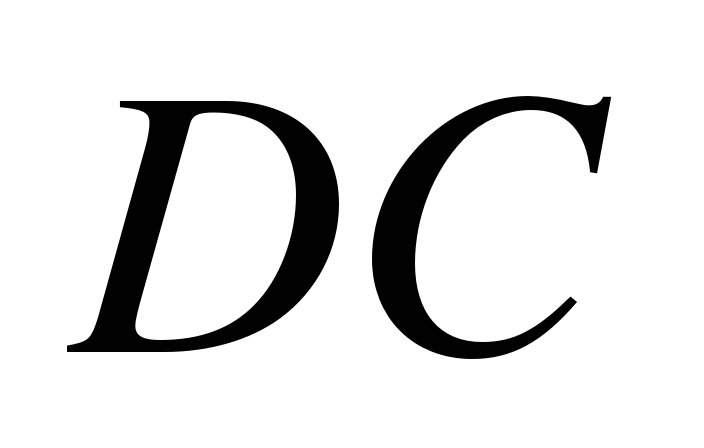 
также пересекают эту плоскость.Если плоскость
параллельна одной из двух параллельных прямых, то она параллельна и другой прямой.Если прямая пересекает некоторую плоскость, то в этой плоскости можно провести прямую, параллельную данной прямой.
Две прямые, параллельные одной плоскости, пересекаются.
Параллельность прямых и плоскостей
Вариант II
Две прямые в пространстве называются параллельными, если они не имеют общих точек.
Если прямая параллельна плоскости, то она пересекает какую-либо прямую, лежащую в плоскости.
Если средняя линия треугольника параллельна плоскости
, то основание треугольника также параллельно этой плоскости.Если прямая
параллельна линии пересечения плоскостей и , то прямая пересекает плоскость Через данную точку пространства можно провести только одну плоскость, параллельную данной прямой.
Если основание ВС трапеции АВСD пересекает некоторую плоскость, то и основание АD также пересекает эту плоскость.
Если две прямые параллельны третьей прямой, то они параллельны.
Две прямые, параллельные одной плоскости, параллельны.
В плоскости
невозможно провести прямую, параллельную прямой , пересекающей плоскость ,Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Тест "Параллельность прямых и плоскостей" (45 KB)
0
849
44
Нравится
0
