Теорема Пифагора

Теорема Пифагора

(разработка урока)

Подготовлена учителем математики ГБОУ ООШ с.Жигули.

Клоковой Татьяной Анатольевной.

Слайд №1

Тип урока – комбинированный.

Слайд №2

Цели урока:

• Познакомить учащихся с теоремой Пифагора и следствиями из нее.

• Научить доказывать теорема Пифагора, применять ее при решении задач.

• Развивать и совершенствовать у учащихся умение применять знания в измененной ситуации.

• Формировать информационно- коммуникативные компетенции.

Оборудование урока:

Интерактивная доска или проектор, инструменты, плакаты с другими доказательствами теоремы Пифагора, карточка №1 (для практической работы) ,

№2 (для первичного закрепления материала).

Ход урока.

1. Организационный момент

Задача: подготовить учащихся к работе. Взаимное приветствие; проверка подготовленности учащихся к работе (рабочее место, внешний вид); концентрация внимания.

2. Актуализация опорных знаний учащихся. Учитель: Сегодня у нас необычный урок, а урок исследования. Нам предстоит измерить длину лестницы, например школьной, зная, что один конец отстоит от стены на 4 м, а второй на стыки стены и крыши. Высота стены 8м.

Слайд № 3

Задаются вопросы классу:

-с какой геометрической фигурой придется работать при решении данной задачи?

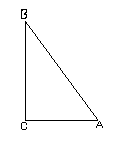
( прямоугольным треугольником)Обозначим его АВС.

- каким отрезком представлена длина лестницы в треугольнике АВС? (гипотенузой АВ).

Перед классом ставится задача:

1) Выполнив чертёж треугольника АВС в тетради и ,работа в парах, в течении 1 мин, вычислить длину лестницы ( отрезк АВ).

2) Проверка полученного результата.

Учитель:

-почему вы не смогли решить данную задачу? (звучат разные ответы) А вот если бы вы знали теорему Пифагора, то смогли бы справиться не только с этой задачей, но и со многими другими. Следовательно основная цель нашего урока – изучение теоремы Пифагора.

Прежде чем приступать к доказательству теоремы вам предстоит в течение трех минут выполнить лабораторную работу.

У вас на столах находится карточка с заданием №1 (задание выполняется письменно, ответы фиксируются в тетрадке.)(карточки в 2 вариантах)

Учитель:

- к какому выводу вы пришли выполняя задания?

Ответы учеников.

( 1вариант. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равно сумме площадей квадратов, построенных на его катетах.

2 вариант. Квадрат гипотенузы равен сумме квадратов катетов )

Учитель:

Вы в результате выполнения лабораторной работы сформулировали теорему Пифагора. Причем 1 вариант сформулировал ее так как она звучала во времена Пифагора.

А 2 вариант сформулировал её в современном варианте.

Слайд №4

Но чтобы теорему Пифагора доказать, нужно все о косинусе знать!

3. Изучение новой темы.

Учитель:

Обратимся снова к треугольнику АВС, который начерчен в тетради.

-как называются отрезки АС и СВ? (катеты)

-чему ровно отношение АС/АВ? СВ/АВ? ( cos A; cos B)

Учитель формулирует теорему и проводит её доказательство на доске. Учащиеся фиксируют доказательство в тетради.

Учитель:

Пифагор- древнегреческий ученый доказал теорему в 6 веке до нашей эры. Теорема была известна еще в древнем Египте и Вавилоне. В настоящее время известно более 100 ее доказательств. Сегодня вы узнаете об еще одном доказательстве( один из учеников заранее готовит сообщение о доказательстве теоремы предложенном индийскими математиками и знакомит с ними класс).

Слайд №5

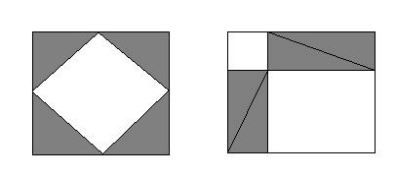
Ученик:

Здесь один и тот - же большой квадрат разрезан на части двумя разными способами. Треугольники слева одни и те же поэтому не заштрихованный квадрат слева равновелик двум не заштрихованным квадратами справа, но квадрат слева построен на гипотенузе, а квадрат справа на катетах этого же треугольника

Учитель:-какие еще открытия совершил Пифагор?

( Доказательство теоремы о сумме углов треугольника. Геометрический способ решения квадратных уравнении. Задача о делении плоскости на правильные многоугольники).

Слайд №6

4.Закрепление изученного.

1) Задание классу:

Вам дана карточка с задание №2. Необходимо заполнить пустые клеточки, причем задание выполняется в тетради, затем ответ заносится в карточку( после выполнения работы проводится взаимопроверка. )

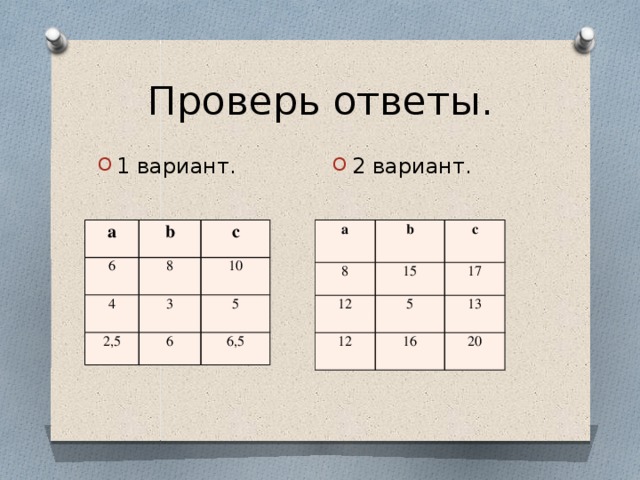
Ответы представлены на слайде.

Слайд № 7

2)Вернемся к задаче, которая не была решена нами ранее « Найти длину лестницы…». Все работают самостоятельно, один ученик у доски решает задачу.

Затем решение задач №6(1), 7 тетради.

Два ученика работают у доски.

5.Итоги урока.

1) Подводя итоги урока еще раз проговаривается формулировка теоремы.

Учитель:Значение теоремы состоит в том, что с её помощью выводятся все теоремы, касающиеся связи сторон и углов в треугольнике. Все треугольники, у которых стороны пропорциональны числам 3,4,5 называются пифагоровыми, а треугольник со сторонами 3м,4м,5м называют Египетским, потому что его модель из бечевы египтяне применяли для построения прямого угла на плоскости.

Слайд №7

2)Предлагается вернуться к цели урока и каждому ответить на вопрос:

-чему я научился сегодня?

- что нового я узнал ?

Учащимся сообщается домашнее задание с кратким инструктажем по его выполнению параграф 7 п. 63,64 воп. стр. 93 №3,4 задачи №2(1),3(1),10

Учитель:

В заключение я хочу познакомить вас с некоторыми заповедями учеников пифагорейской школы:

1) Делай лишь то, что впоследствии не осиротит тебя и не заставит раскаиваться;

2) Не делай никогда то, чего не знаешь, но научись всему, что нужно знать;

3) Не пренебрегай здоровьем своего тела;

4) Либо молчи, либо говори то, что ценнее молчания;

Слайд №8

Слайд №9

И еще: Измеряй свои желания, взвешивай свои мысли, исчисляй свои слова!

Слайд №10

До свидания!

Карточка №1

1 вариант.

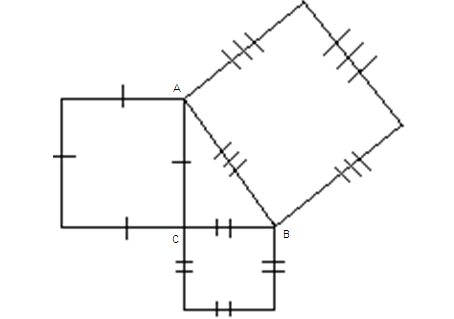
Катеты прямоугольного треугольника равны 8см., 15см. Гипотенуза равна 17 см.

Задание.

1.Найдите площади квадратов, построенных на катетах и на гипотенузе.

2. Найдите сумму площадей квадратов.

Карточка №1

2 вариант

Катеты прямоугольного треугольника равны 2,5см., 6см. Гипотенуза равна 6,5 см.

Задание.

1.Найди квадраты гипотенузы, катетов.

2.Найди сумму квадратов катетов, и сравни это значение с квадратом гипотенузы.

3.Запиши вывод.

3.Запиши вывод

Карточка №2.

1 вариант.

Задание.

Заполни пустые клеточки таблицы.

Карточка №2.

2 вариант.

Задание.

Заполни пустые клеточки таблицы.

Теорема Пифагора.

Пифагор Самосский (лат. Pythagoras; 570 - 490 гг. до н. э.) - древнегреческий философ и математик .

Цели урока:

• Познакомиться с теоремой Пифагора и следствиями из нее.
• Научиться доказывать теорему Пифагора, применять ее при решении задач.

Задача.

• Измерить длину лестницы зная, что один конец отстоит от стены на 4 м, а второй на стыки стены и крыши. Высота стены 8м .

Формулировка теоремы .

звучала во времена Пифагора

в современном варианте.

• Площадь квадрата, построенный на гипотенузе прямоугольного треугольника, равно сумме площадей квадратов, построенных на его катетах.

• Квадрат гипотенузы равен сумме квадратов катетов

Доказательстве теоремы предложенное индийскими математиками

• Здесь один и тот - же большой квадрат разрезан на части двумя разными способами. Треугольники слева одни и те же поэтому не заштрихованный квадрат слева равновелик двум не заштрихованным квадратами справа, но квадрат слева построен на гипотенузе, а квадраты справа на катетах этого же треугольника

Проверь ответы.

• 2 вариант.

• 1 вариант.

a

a

6

8

b

b

15

c

12

8

4

c

2,5

12

10

17

5

3

16

6

13

5

6,5

20

Открытия Пифагора

• Доказательство теоремы о сумме углов треугольника.
• Геометрический способ решения квадратных уравнении.
• Задача о делении плоскости на правильные многоугольники.

Заповеди учеников Пифагорейской школы:

• 1) Делай лишь то, что впоследствии не осиротит тебя и не заставит раскаиваться;
• 2) Не делай никогда то, чего не знаешь, но научись всему, что нужно знать;
• 3) Не пренебрегай здоровьем своего тела;
• 4) Либо молчи, либо говори то, что ценнее молчания.

Мои пожелания .

Измеряй свои желания, взвешивай свои мысли, исчисляй свои слова!

До свидания!