"Теорема Пифагора" презентация

Подготовила учитель математики МБОУ-СОШ №2 им.А.И.Герцена г.Клинцы Гетун Т.А.

Пифагор Самосский

Пифагор Самосский

• Пифагорейцами было сделано много важных открытий в арифметике и геометрии.

«Ослиный мост»

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum «ослиный мост» или elefuga - «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.

Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.

Вопросы

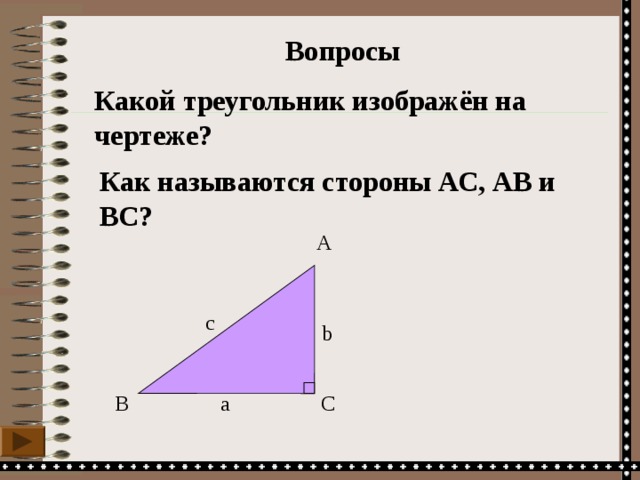
Какой треугольник изображён на чертеже?

Как называются стороны АС, АВ и ВС?

A

с

b

B

a

C

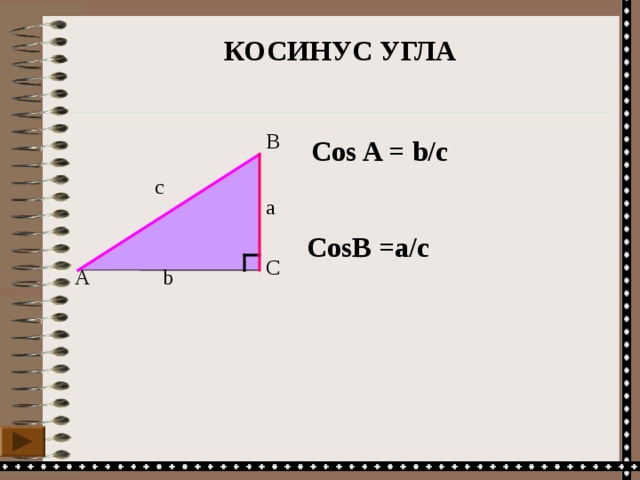
КОСИНУС УГЛА

B

C os A = b/c

c

a

CosB =a/c

C

A b

5

Площадь квадрата

S= a ²

a

a

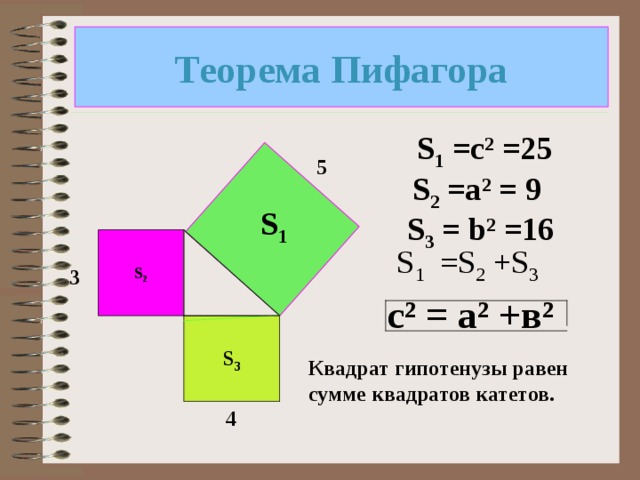
Теорема Пифагора

S 1 =c ² =25

5

S 2 =a ² = 9

S 1

S 3 = b ² =16

S 2

S 1 =S 2 +S 3

3

с ² = а ² +в ²

S 3

Квадрат гипотенузы равен сумме квадратов катетов.

4

Итак,

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим -

И таким простым путем

К результату мы придем.

Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же “ветряной мельницей”, составляли стихи вроде “Пифагоровы штаны на все стороны равны”, рисовали карикатуры.

Шаржи из учебника XVI века

Ученический шарж XIX века

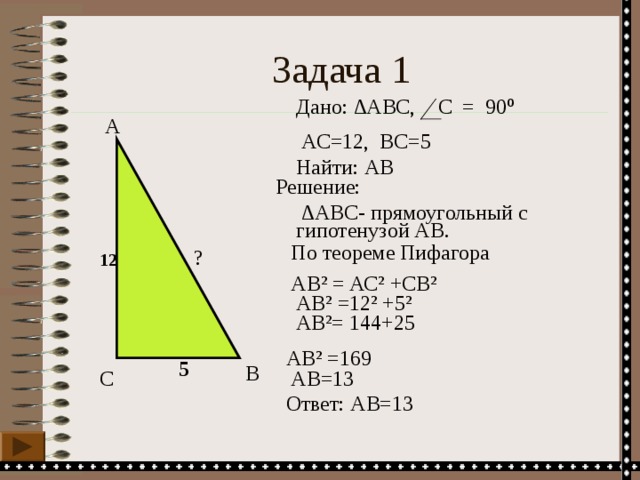
Задача 1

Дано: ∆АВС,

C = 90 º

А

AC=12, BC=5

Найти: АВ

Решение:

∆ АВС - прямоугольный с гипотенузой АВ.

По теореме Пифагора

АВ ² = АС ² +СВ ²

?

12

АВ ² =12 ² +5 ²

АВ²= 144+25

АВ ² =169

5

В

АВ=13

С

Ответ: АВ=13

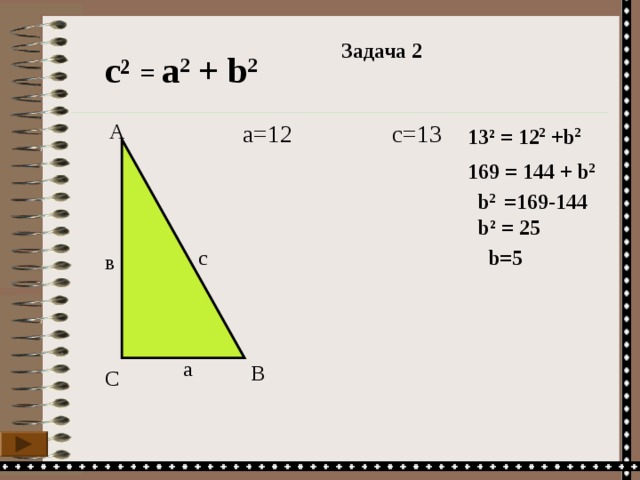
Задача 2

с ² = а 2 + b 2

а=12

А

с= 13

13 ² = 12 2 + b 2

169 = 144 + b 2

b 2 =169-144

b ² = 25

с

b=5

в

а

В

С

Часто математики записывали свои задачи в стихотворной форме. Вот одна из задач индийского математика XII века Бхаскары :

2. На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в том месте река

В четыре лишь фута была широка.

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?

Решение:

3 ² + 4² = x²

X² = 25

X = 5 (футов) – длина отломленной части ствола;

3 + 5 = 8(футов) – высота тополя.

?

3

4

Домашнее задание:

• п. 63
• «5» - задача №6
• «4» - задача №7
• «3» -задача №2(3),3(3).

Итог урока

• «Сегодня на уроке я повторил…»
• «Сегодня на уроке я узнал…»

• «Сегодня на уроке я научился…»