
Группы 11Ф, 12Ф, 13Ф
Преподаватель Князева С.Е.

2
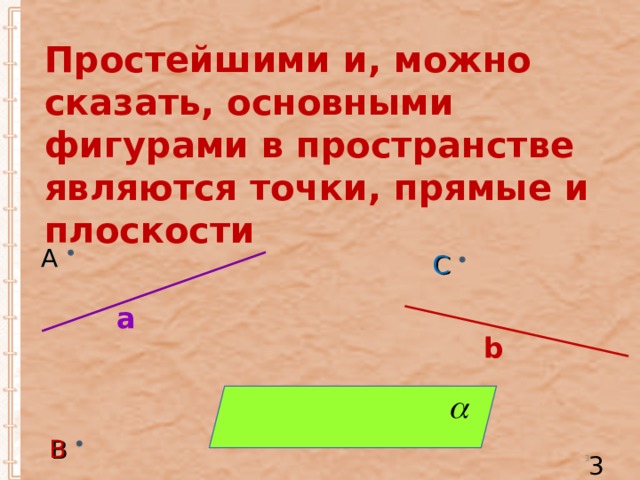
Простейшими и, можно сказать, основными фигурами в пространстве являются точки, прямые и плоскости
А
С
а
b
В
3
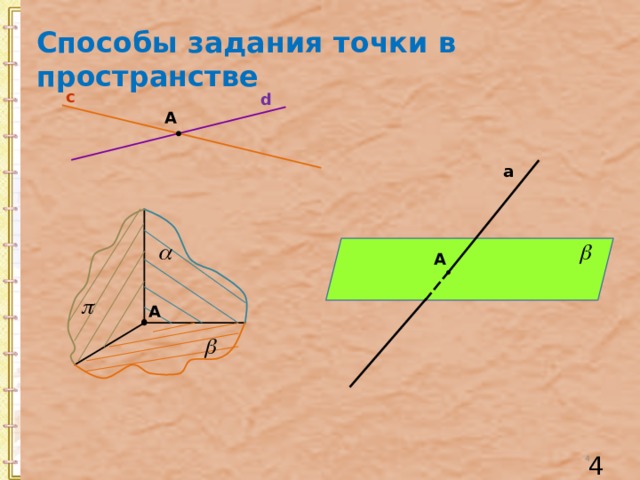
Способы задания точки в пространстве
с
d
А
a
А
А
4
4
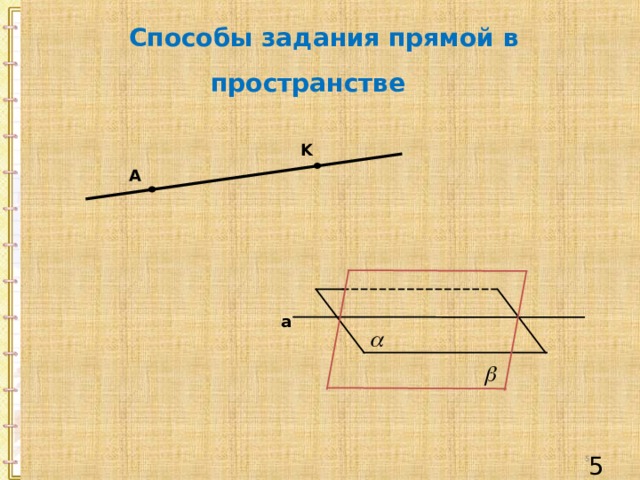
Способы задания прямой в пространстве
K
А
а
5
5
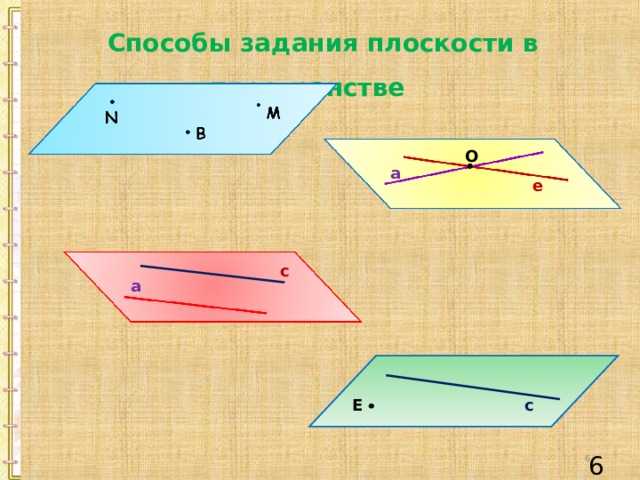
Способы задания плоскости в пространстве
O
a
e
c
a
c
E
6
6

6

Координатной прямой называется прямая, на которой выбрано начало отсчета (т. О ) – начало координат, единичный вектор, указывающий положительное направление координатной прямой и школу деления.
-1
x
O
1
8
7
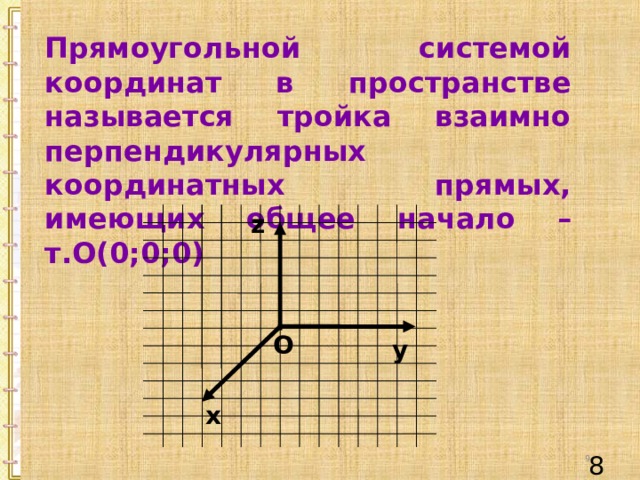
Прямоугольной системой координат в пространстве называется тройка взаимно перпендикулярных координатных прямых, имеющих общее начало – т.О(0;0;0)
z
O
y
х
9
8
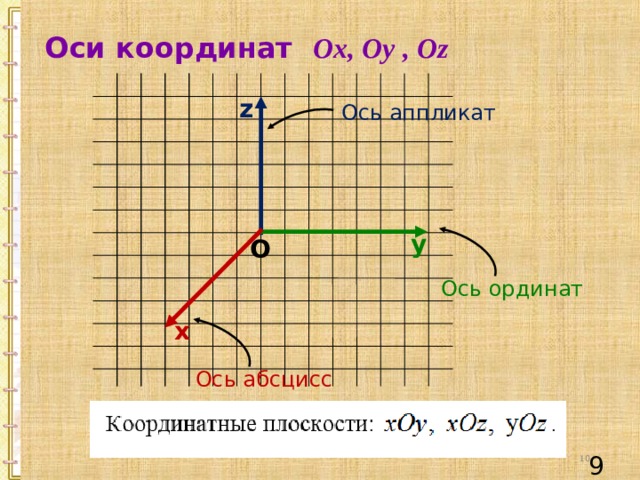
Оси координат Ox, Oy , Oz
z
Ось аппликат
y
O
Ось ординат
х
Ось абсцисс
10
9
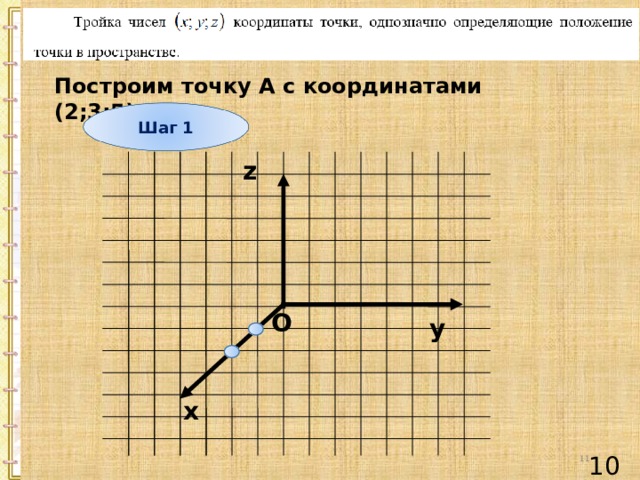
Построим точку А с координатами (2;3;5)
Шаг 1
z
O
y
х
11
10
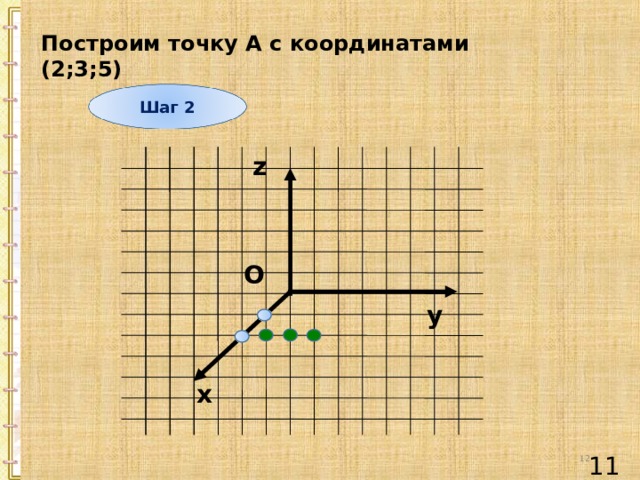
Построим точку А с координатами (2;3;5)
Шаг 2
z
O
y
х
12
11
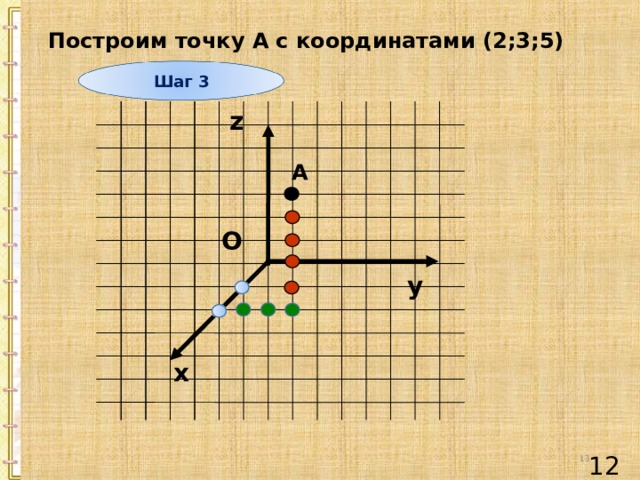
Построим точку А с координатами (2;3;5)
Шаг 3
z
А
O
y
х
13
12
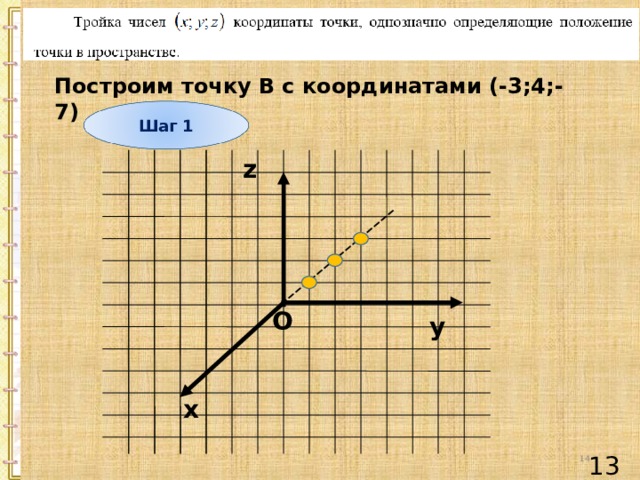
Построим точку В с координатами (-3;4;-7)
Шаг 1
z
O
y
х
14
13
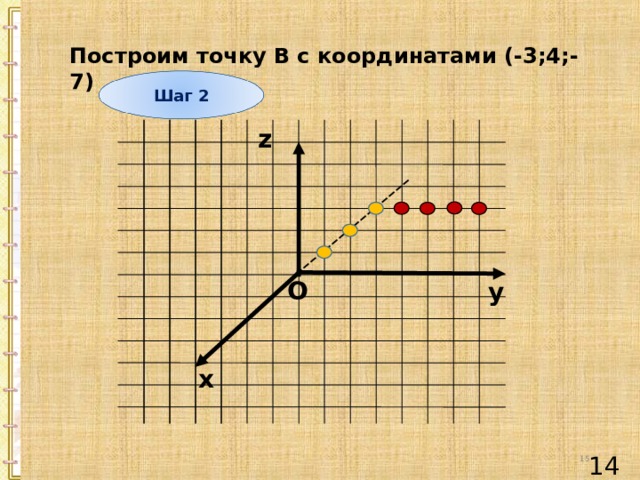
Построим точку В с координатами (-3;4;-7)
Шаг 2
z
O
y
х
15
14
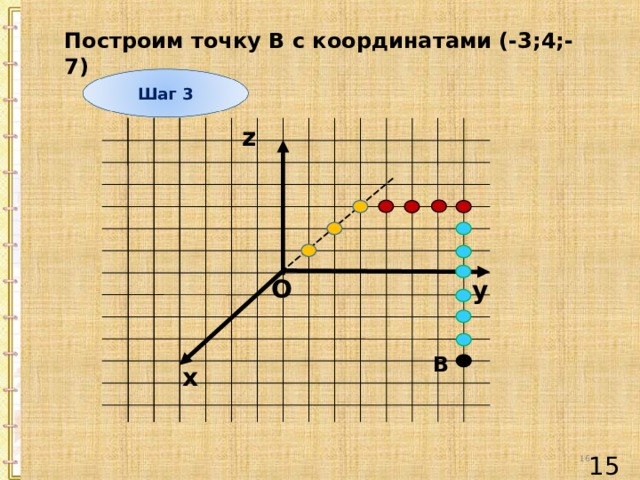
Построим точку В с координатами (-3;4;-7)
Шаг 3
z
O
y
В
х
16
15

16
16

Термин вектор (от лат. Vector - “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона
Уи́льям Ро́уэн Га́мильтон
1805 — 1865
выдающийся ирландский математик и физик XIX века.
17
16
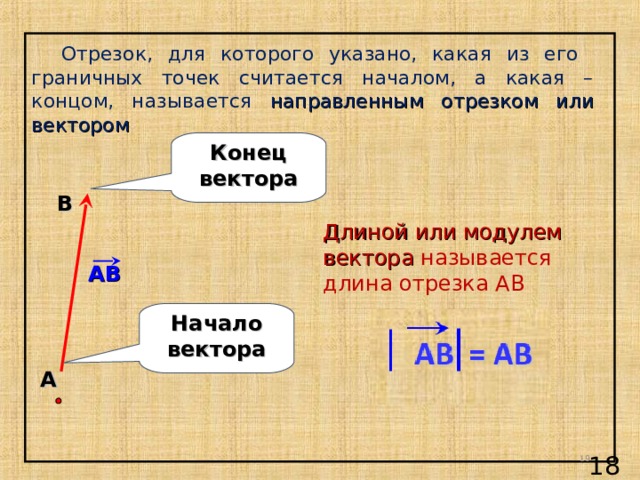
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором
Конец вектора
В
Длиной или модулем вектора называется длина отрезка АВ
АВ
Начало вектора
А
19
18
19
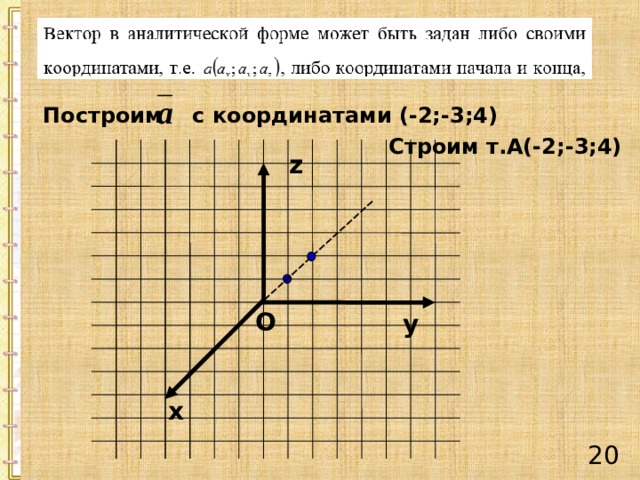
Построим с координатами (-2;-3;4)
Строим т.А(-2;-3;4)
z
O
y
х
19
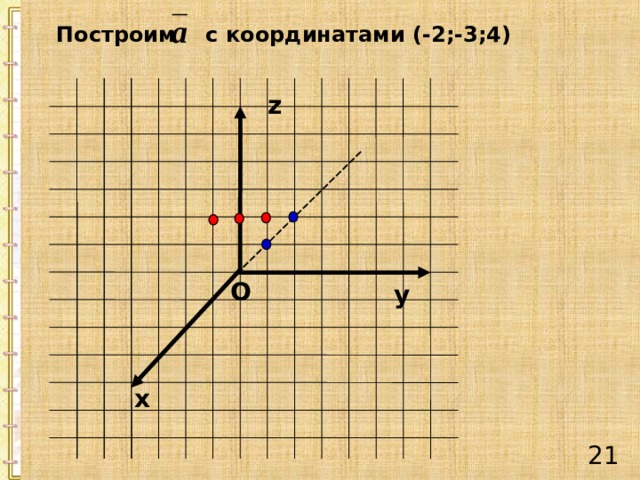
Построим с координатами (-2;-3;4)
z
O
y
х
20
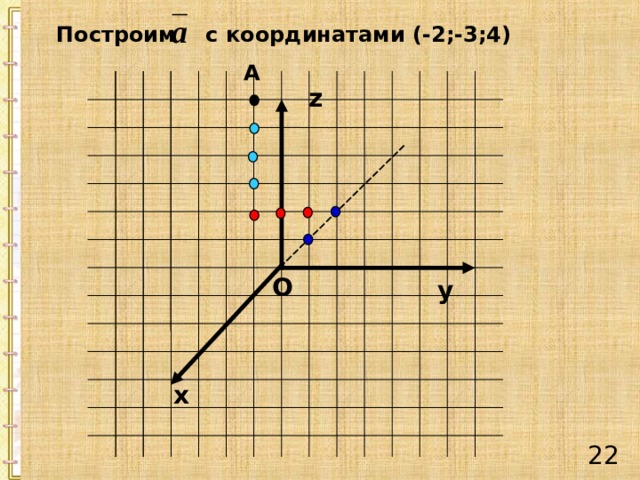
Построим с координатами (-2;-3;4)
А
z
O
y
х
21
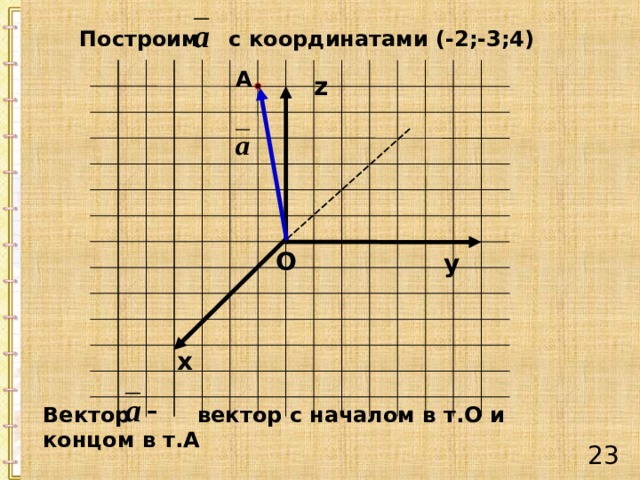
Построим с координатами (-2;-3;4)
А
z
O
y
х
Вектор вектор с началом в т.О и концом в т.А
22
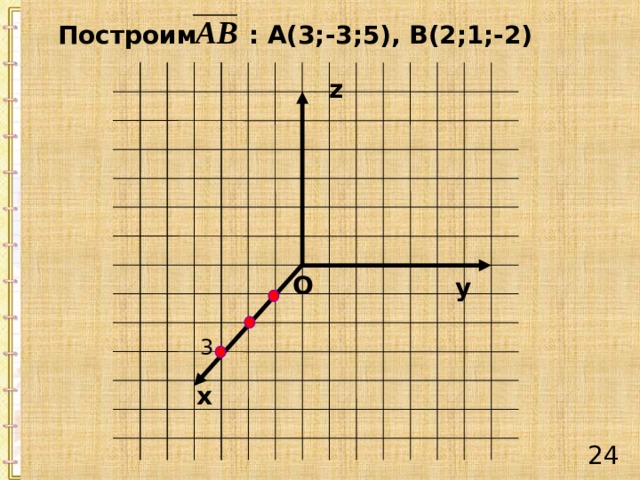
Построим : А(3;-3;5), В(2;1;-2)
z
O
y
3
х
23
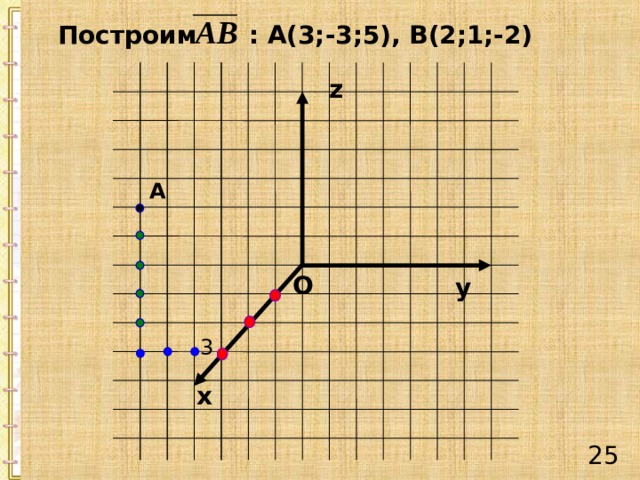
Построим : А(3;-3;5), В(2;1;-2)
z
А
O
y
3
х
24
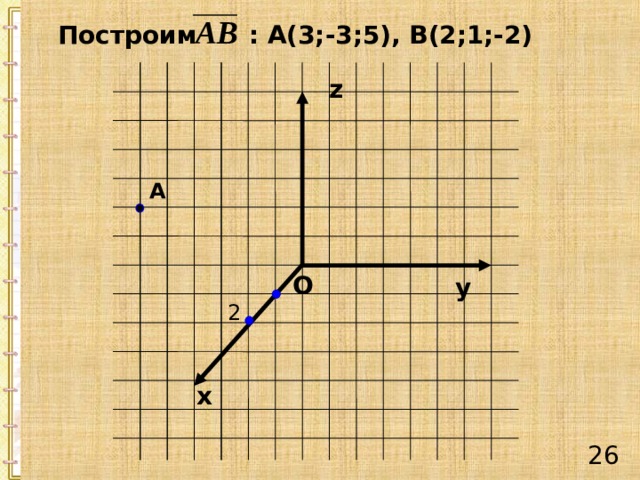
Построим : А(3;-3;5), В(2;1;-2)
z
А
O
y
2
х
25
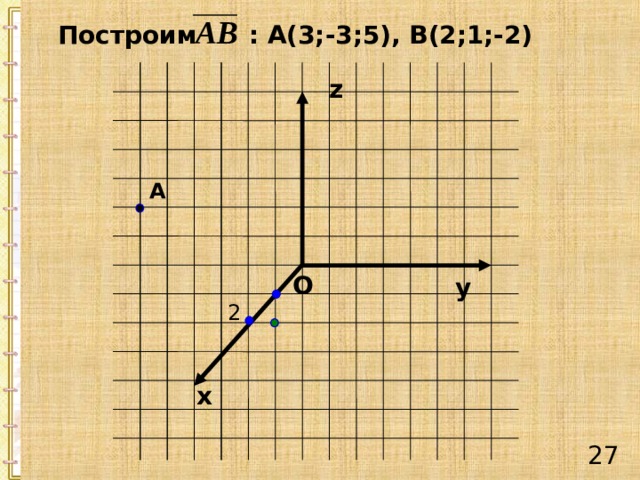
Построим : А(3;-3;5), В(2;1;-2)
z
А
O
y
2
х
26
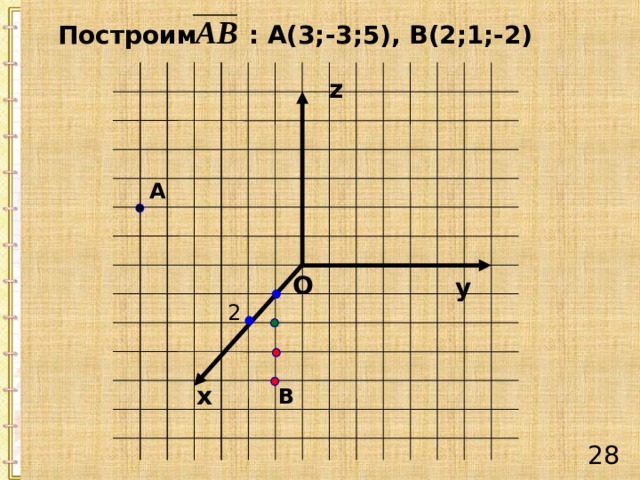
Построим : А(3;-3;5), В(2;1;-2)
z
А
O
y
2
х
В
27
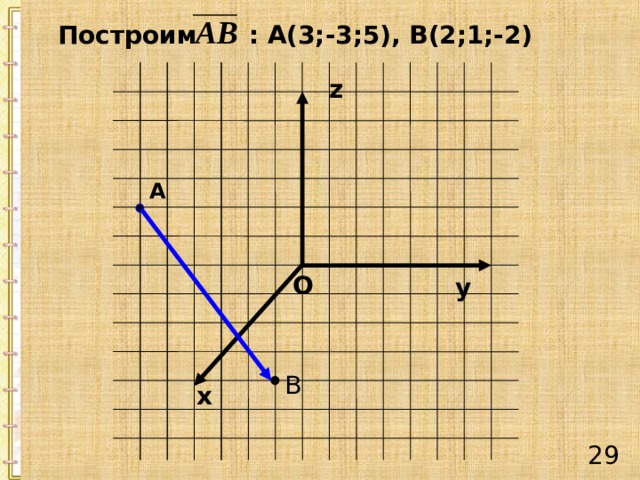
Построим : А(3;-3;5), В(2;1;-2)
z
А
O
y
В
х
28

29

Любая точка плоскости также является вектором. В этом случае вектор называется нулевым
Вектор
MM
M
0
Вектор
Длина нулевого считается равной нулю
«Геометрия 7-9» Л.С. Атанасян и др.
MM = 0
31

Единичный вектор – это вектор, длина которого равна одному
О M = 1
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
31
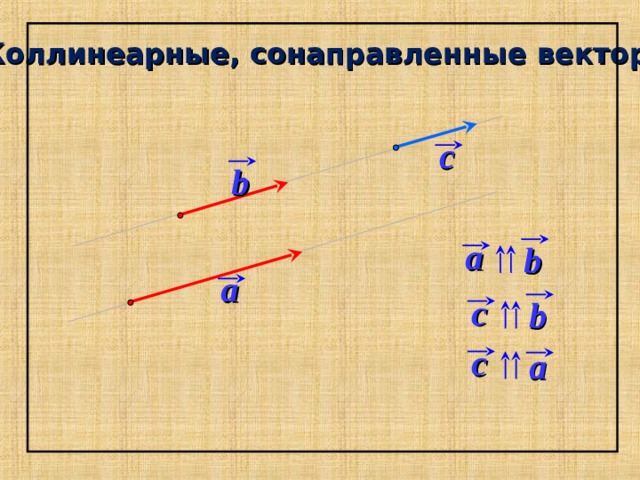
Коллинеарные, сонаправленные векторы
c
b
a
b
a
c
b
«Геометрия 7-9» Л.С. Атанасян и др.
c
a
33
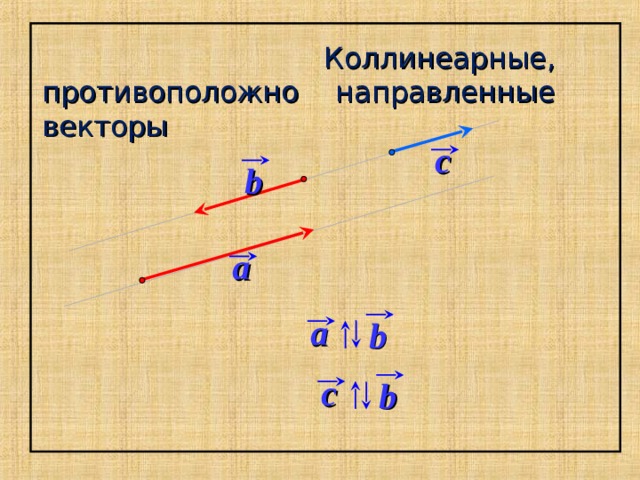
Коллинеарные, противоположно направленные векторы
c
b
a
a
«Геометрия 7-9» Л.С. Атанасян и др.
b
c
b
34

Нулевой вектор считается коллинеарным, сонаправленным и противоположно направленным с любым вектором.
o
o
o
a
c
b
Равные вектора – это сонаправленные вектора, имеющие равную длину
«Геометрия 7-9» Л.С. Атанасян и др.
a
b
a
b
=
a
b
=
35
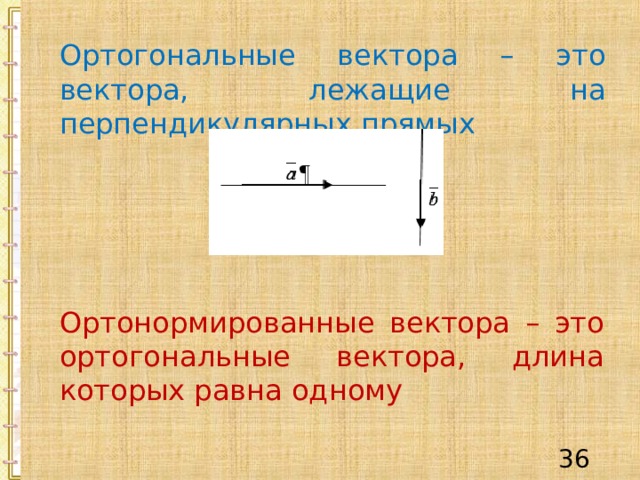
Ортогональные вектора – это вектора, лежащие на перпендикулярных прямых
Ортонормированные вектора – это ортогональные вектора, длина которых равна одному
35
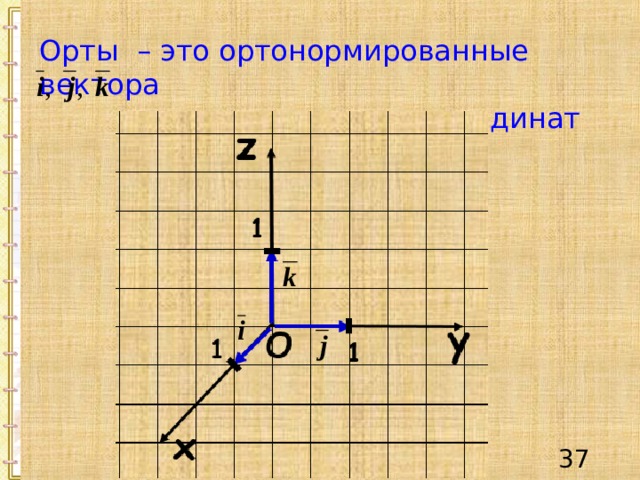
Орты – это ортонормированные вектора
, лежащие на осях координат
35

Если вектор задан своими координатами
, то
Например,
, тогда
В этом случае говорят, что вектор записан в ортах
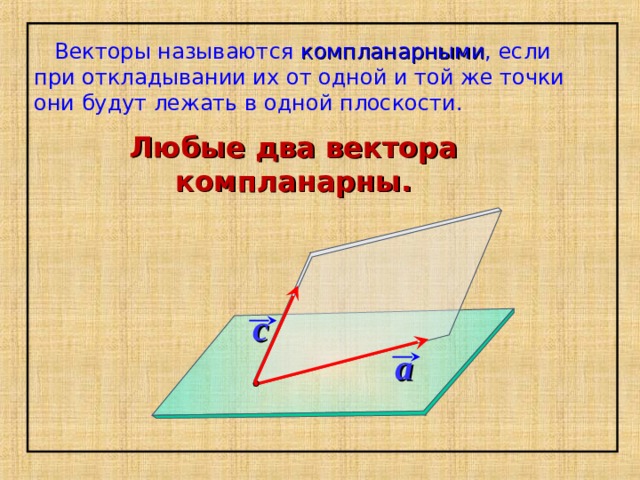
Векторы называются компланарными , если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Любые два вектора компланарны.
c
«Геометрия 10-11» Л.С. Атанасян и др.
a
39
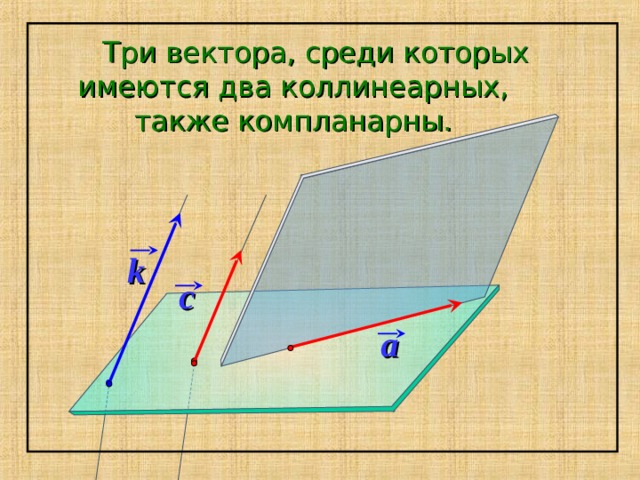
Три вектора, среди которых имеются два коллинеарных, также компланарны.
k
c
«Геометрия 10-11» Л.С. Атанасян и др.
a
40

40

Умножение вектора на число
1
40
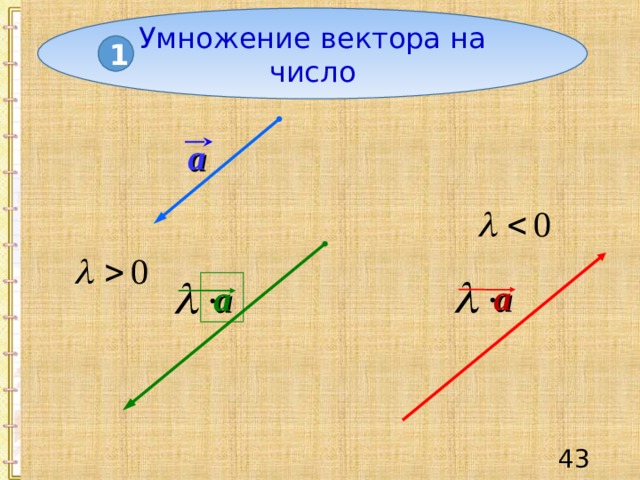
Умножение вектора на число
1
a
a
a
42

Сложение векторов
2
43

Сложение векторов
Правило треугольника
2
b
a
44
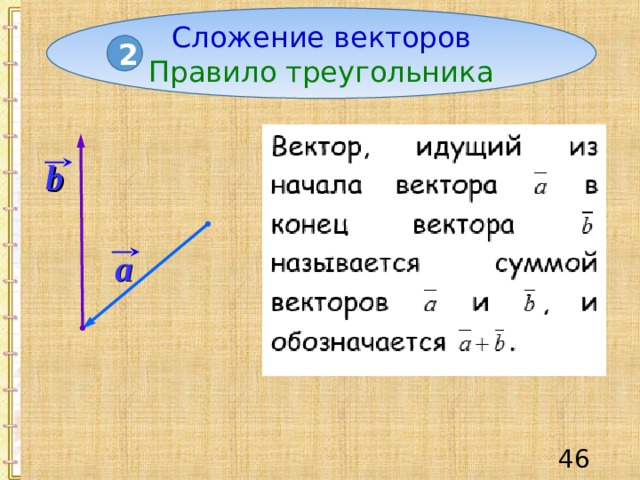
Сложение векторов
Правило треугольника
2
b
a
45
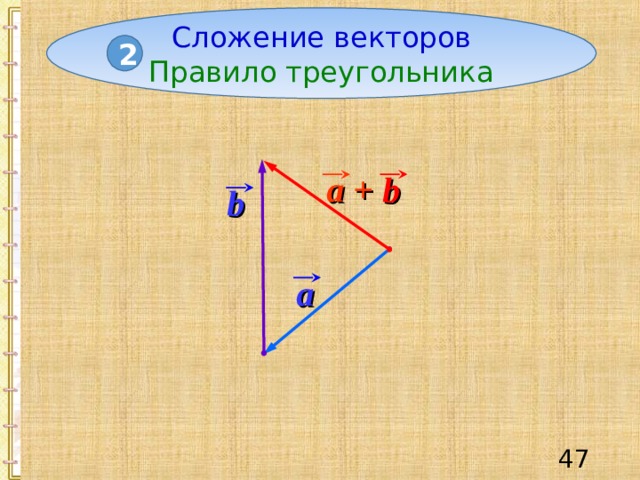
Сложение векторов
Правило треугольника
2
a +
b
b
a
46
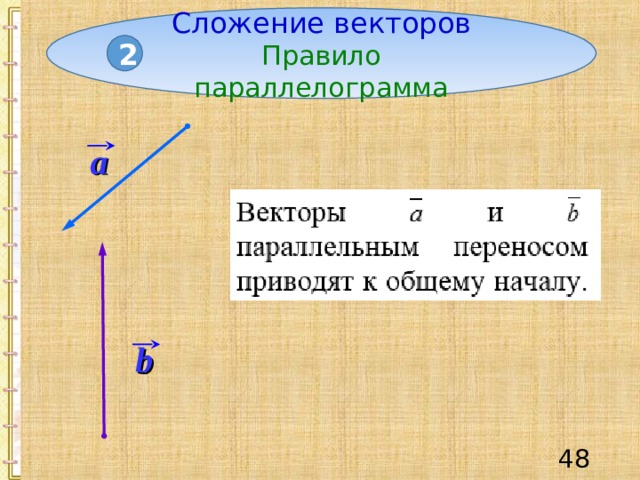
Сложение векторов
Правило параллелограмма
2
a
b
47
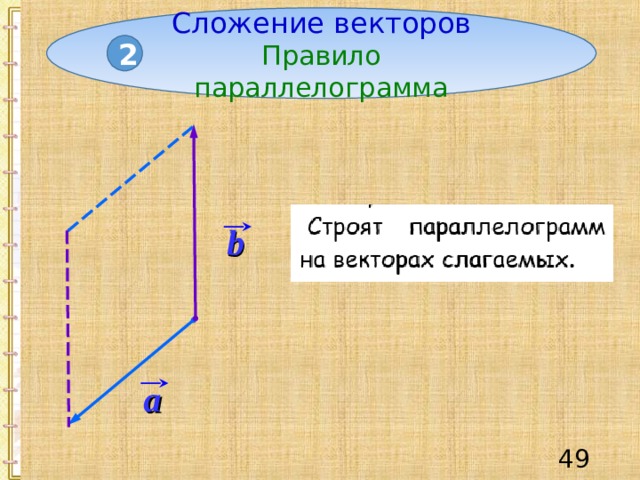
Сложение векторов
Правило параллелограмма
2
b
a
48
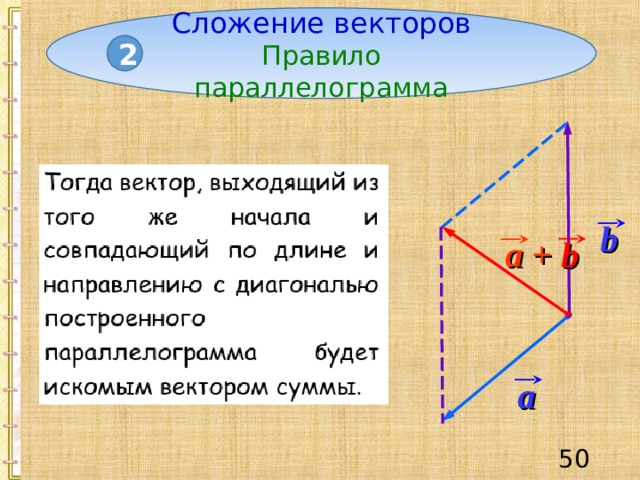
Сложение векторов
Правило параллелограмма
2
b
a +
b
a
49
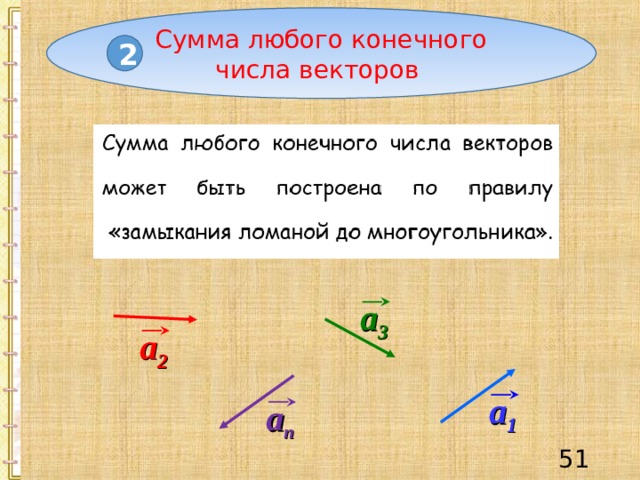
Сумма любого конечного числа векторов
2
a 3
a 2
a 1
a n
50
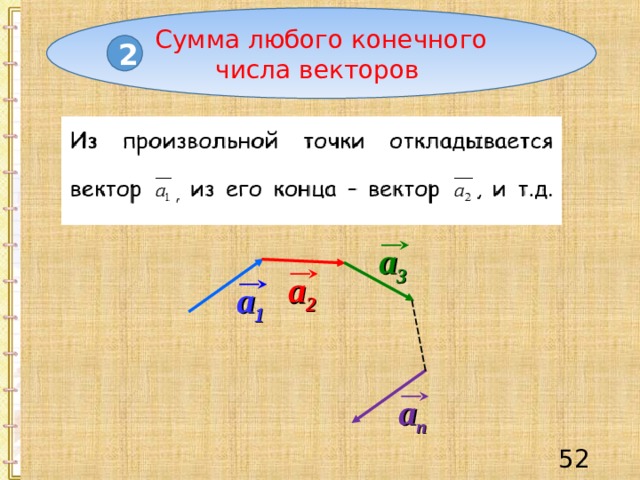
Сумма любого конечного числа векторов
2
a 3
a 2
a 1
a n
51
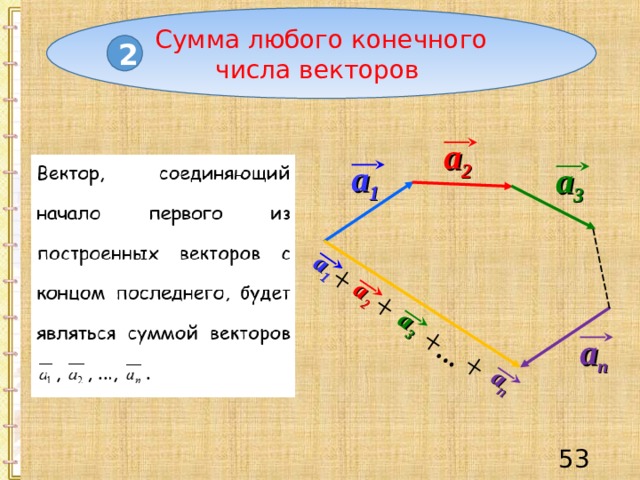
a n
a 2
a 1
a 3
Сумма любого конечного числа векторов
2
a 2
a 1
a 3
a n
52

Вычитание векторов
3
53
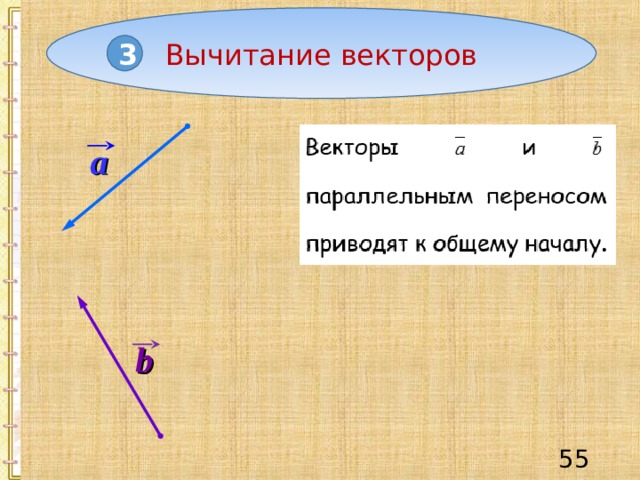
Вычитание векторов
3
a
b
53
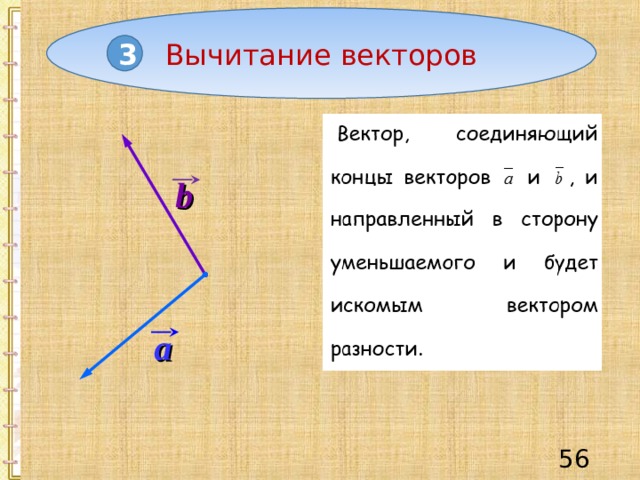
Вычитание векторов
3
b
a
55
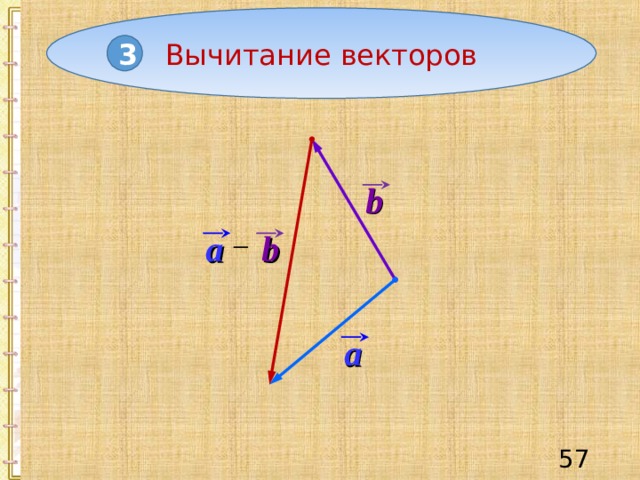
Вычитание векторов
3
b
b
a
a
56

Пример 1
57
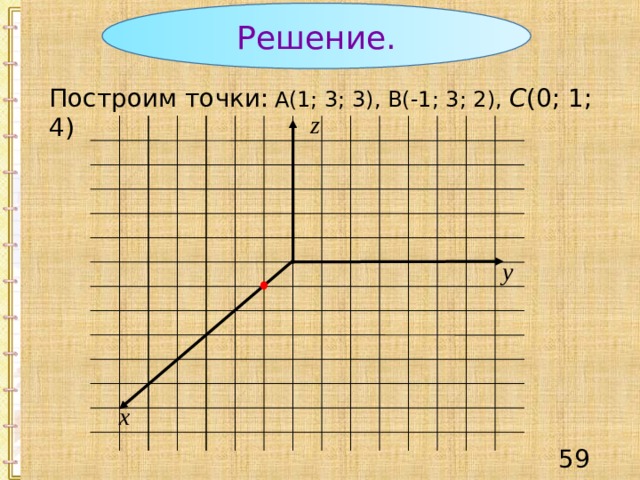
Решение.
Построим точки: А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
y
x
57
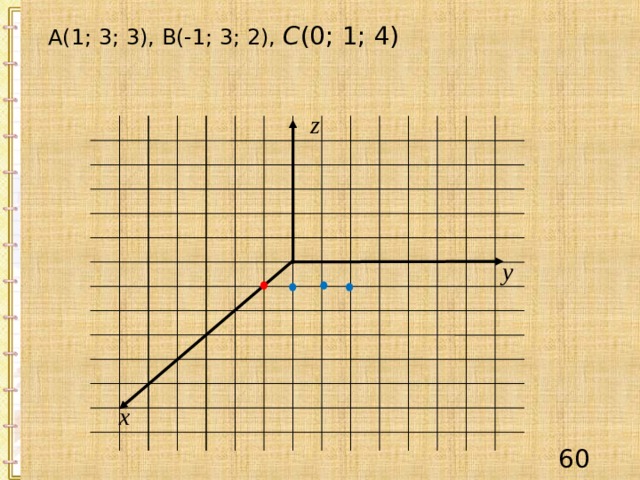
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
y
x
57
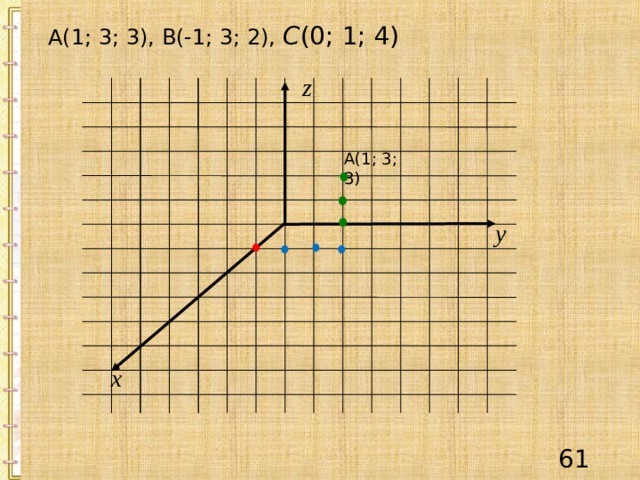
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
А(1; 3; 3)
y
x
57
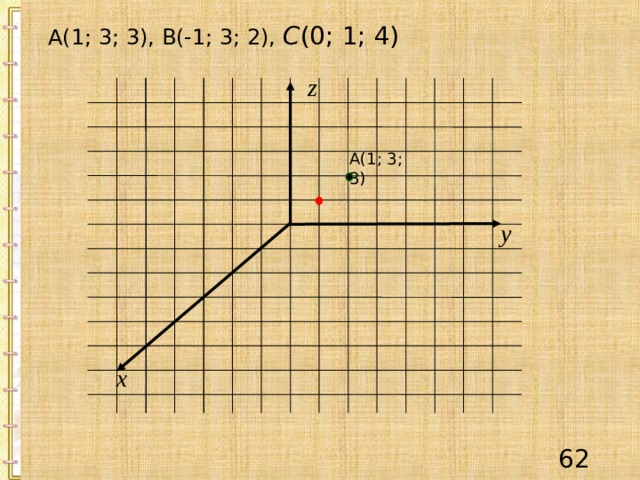
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
А(1; 3; 3)
y
x
61
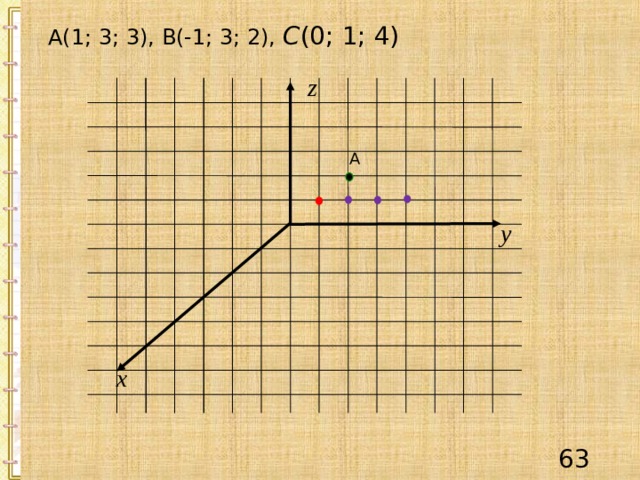
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
А
y
x
62
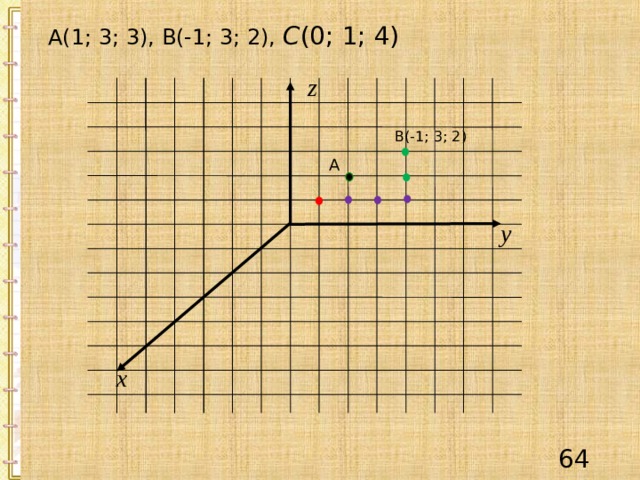
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
В(-1; 3; 2)
А
y
x
63
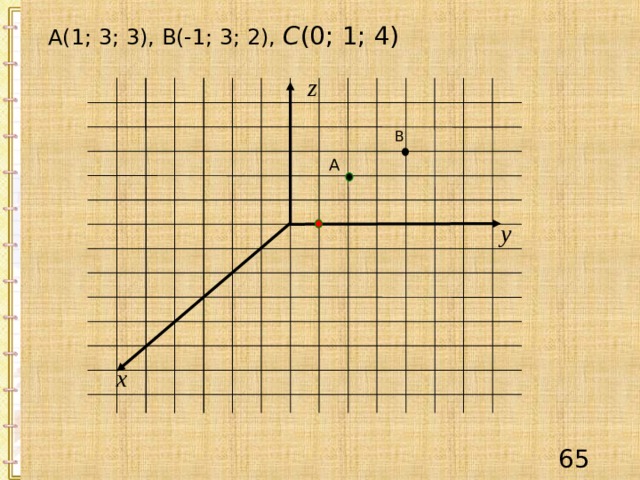
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
В
А
y
x
64
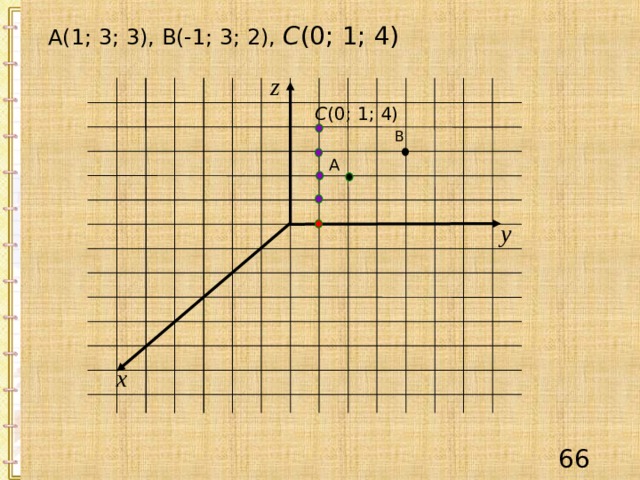
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
z
С (0; 1; 4)
В
А
y
x
65
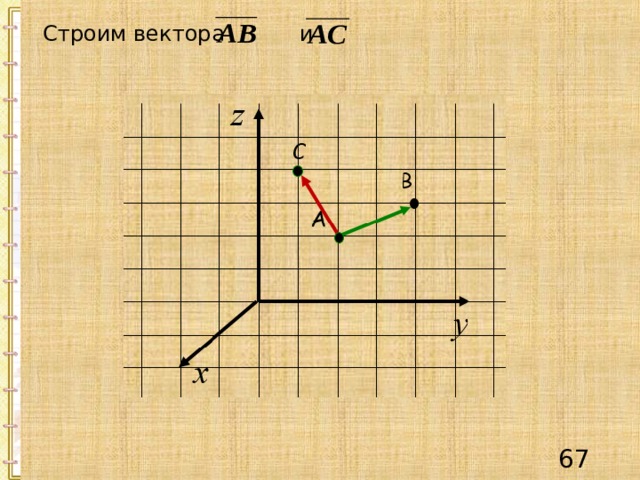
Строим вектора и
66

Запишем вектора и в системе орт.
А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
67

А(1; 3; 3), В(-1; 3; 2), С (0; 1; 4)
67

67

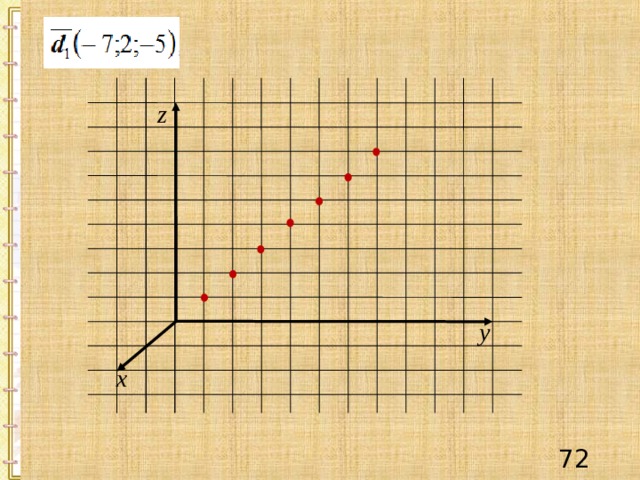
z
y
x
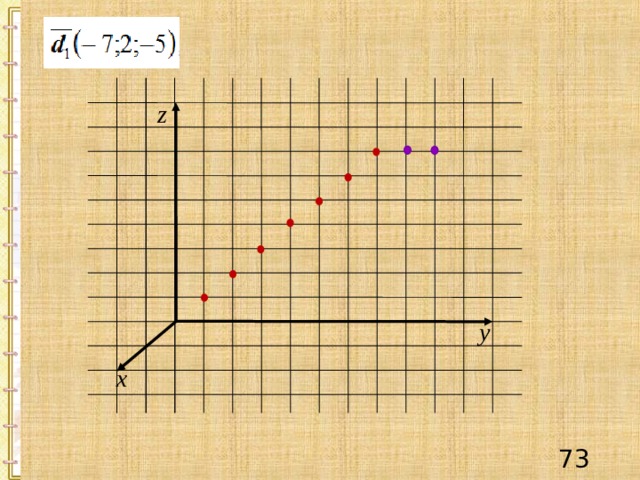
z
y
x
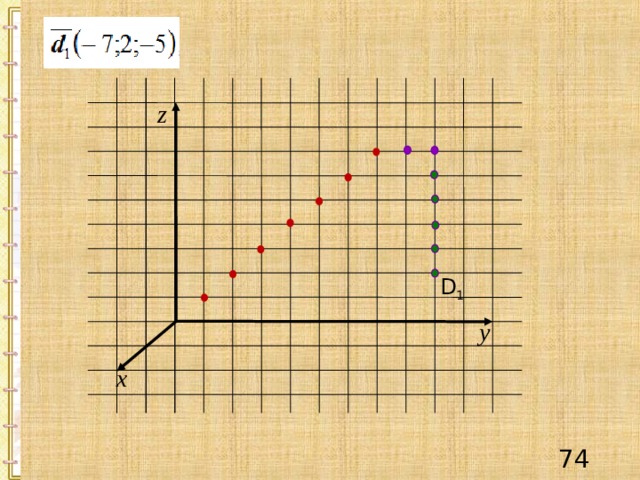
z
D 1
y
x
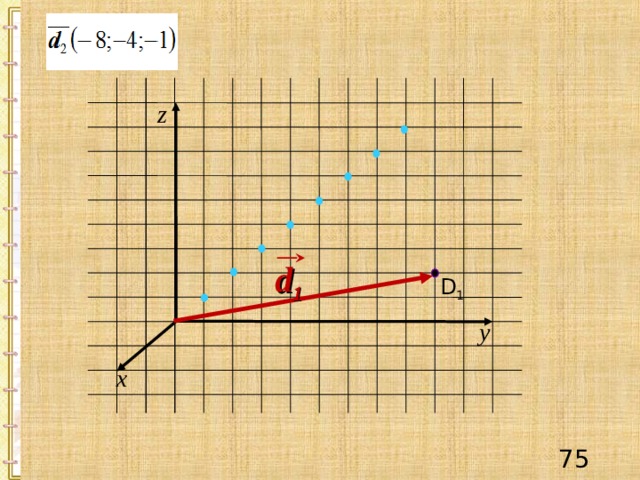
z
d 1
D 1
y
x
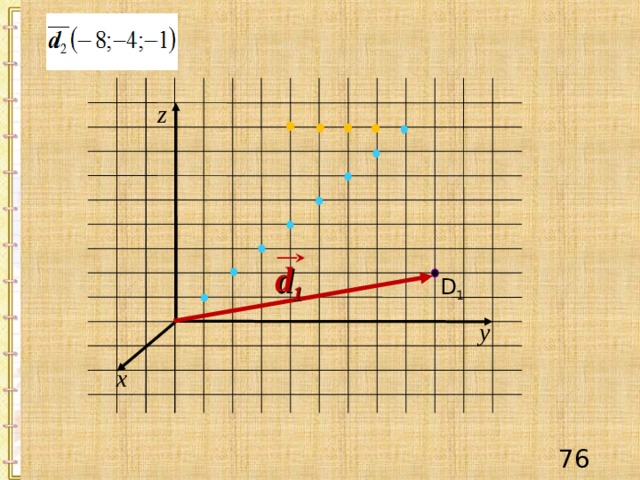
z
d 1
D 1
y
x
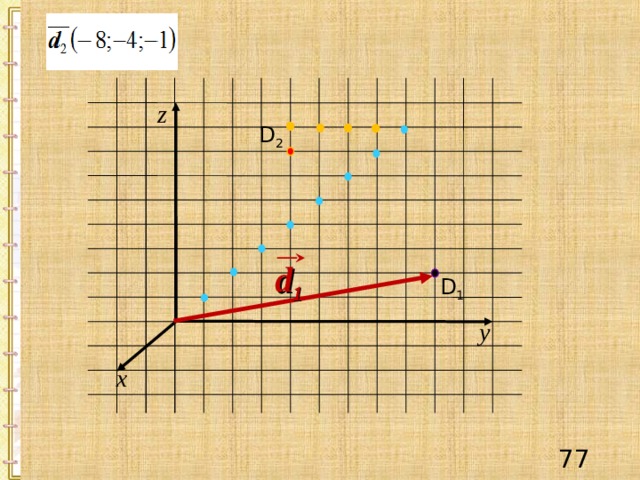
z
D 2
d 1
D 1
y
x
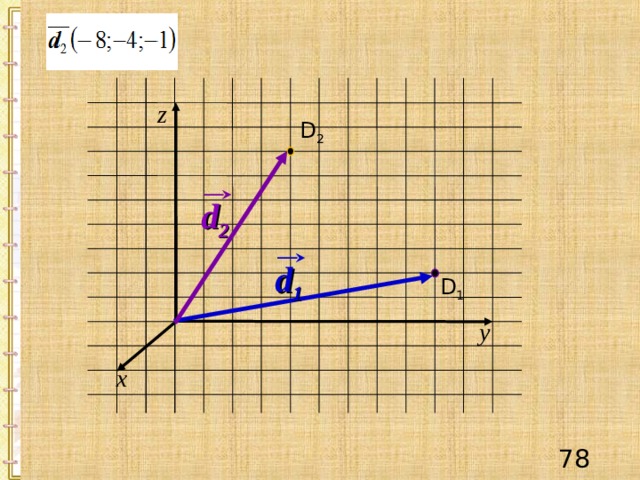
z
D 2
d 2
d 1
D 1
y
x
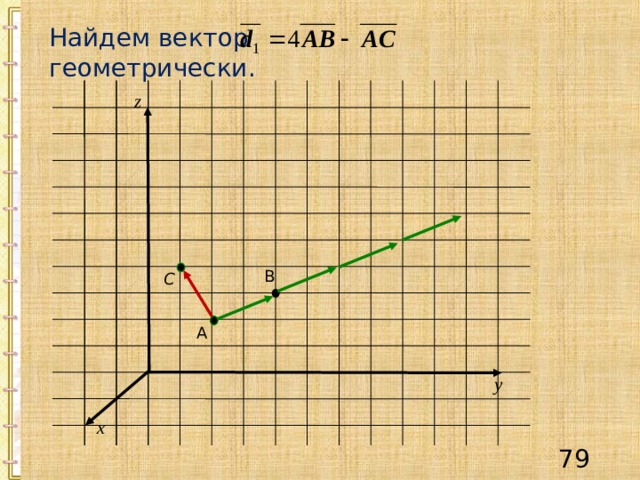
Найдем вектор геометрически.
z
В
С
А
y
x
78
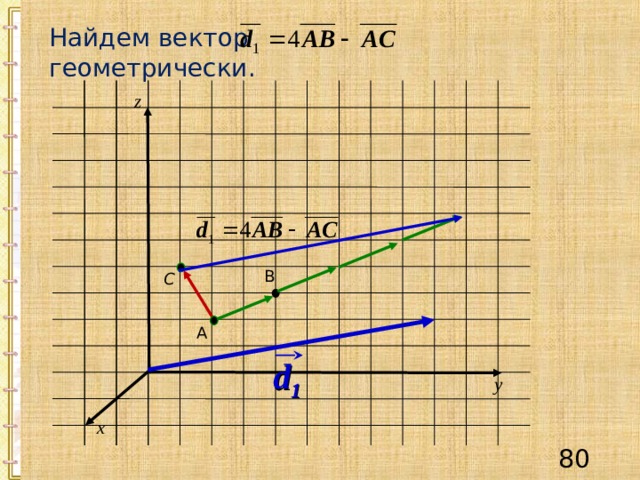
Найдем вектор геометрически.
z
В
С
А
d 1
y
x
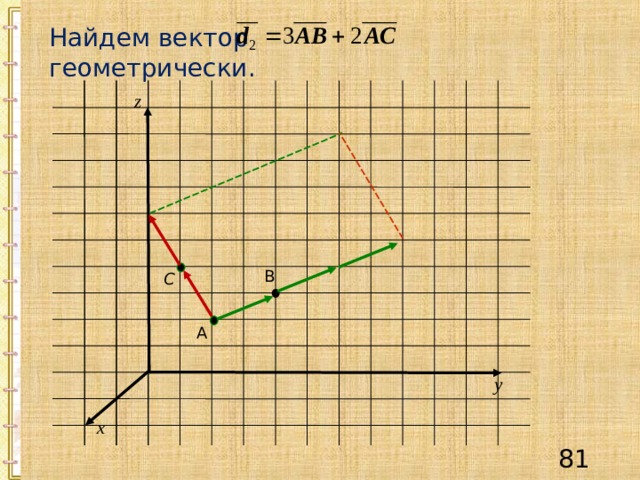
Найдем вектор геометрически.
z
В
С
А
y
x
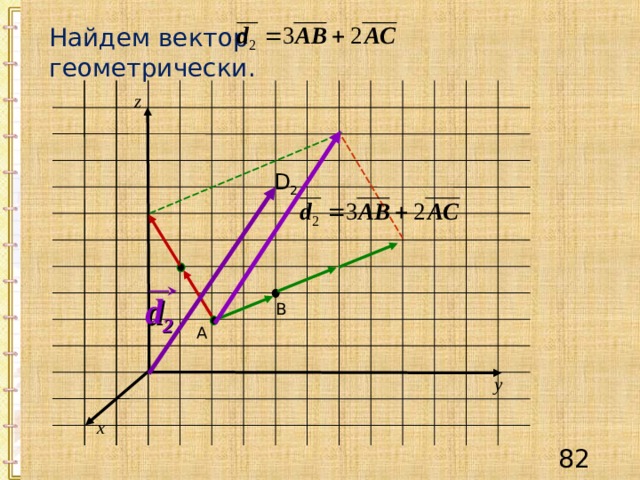
Найдем вектор геометрически.
z
D 2
d 2
В
А
y
x
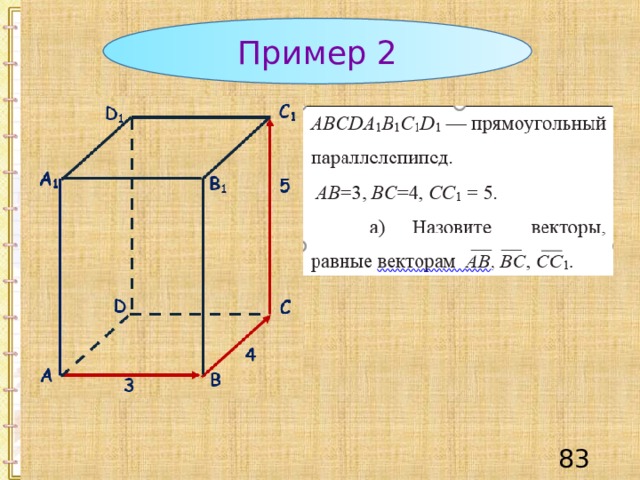
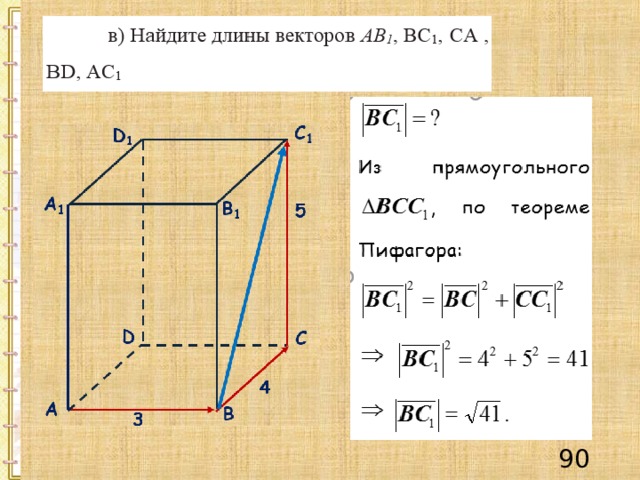
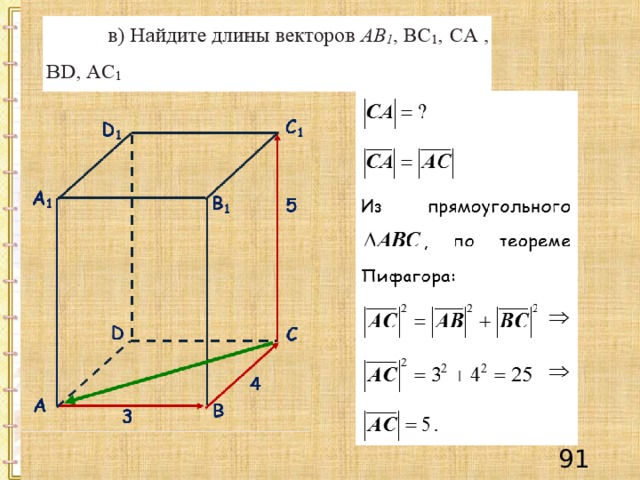
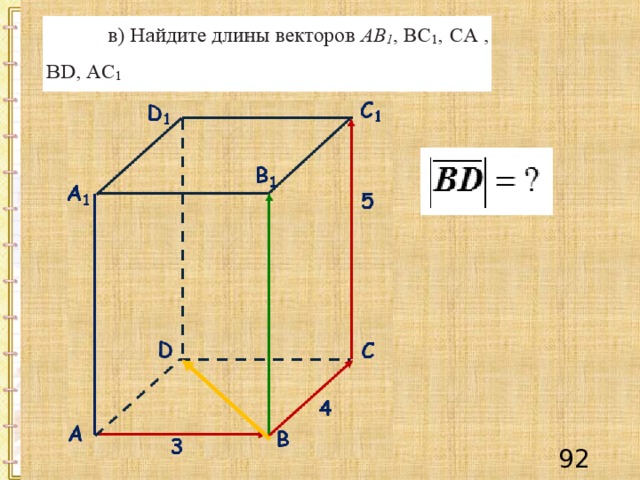
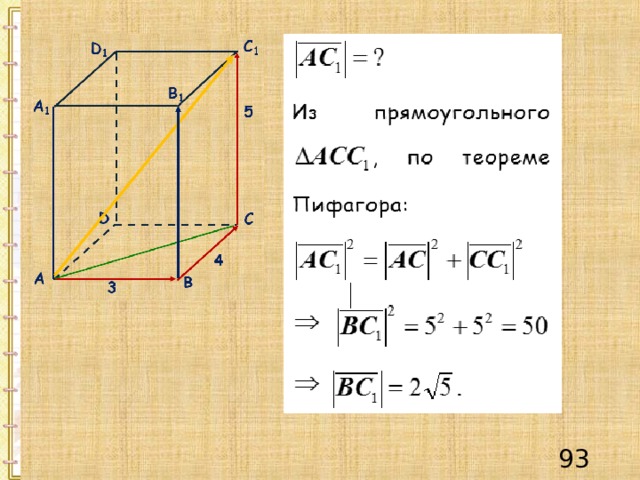
Пример 2
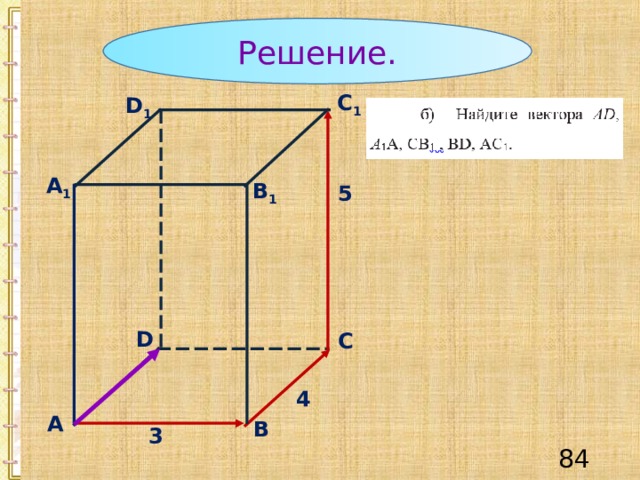
Решение.
С 1
D 1
А 1
B 1
5
D
С
4
А
В
3
С 1
D 1
А 1
B 1
5
D
С
4
А
В
3
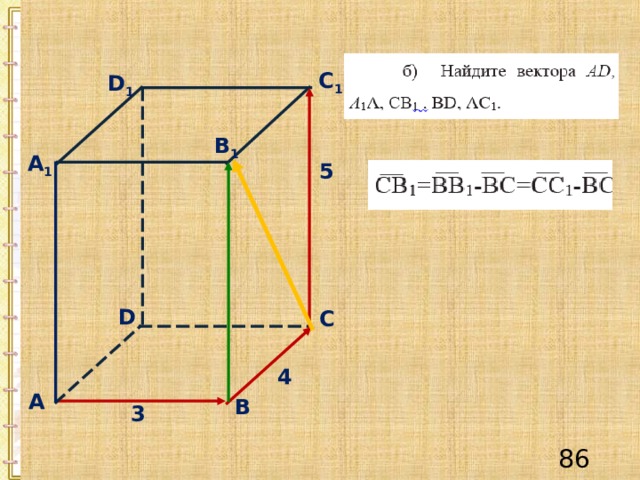
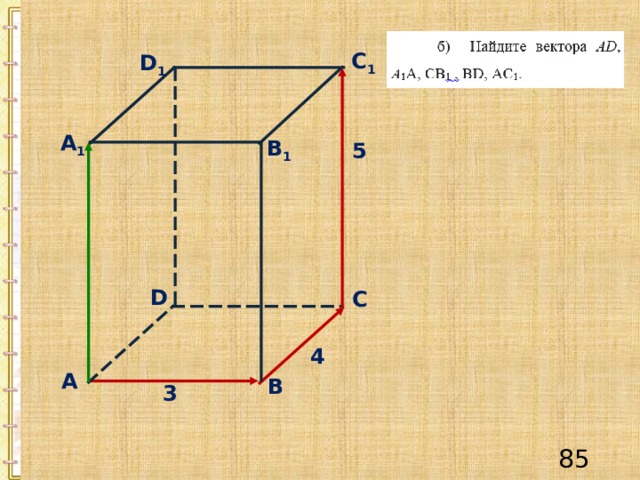
С 1
D 1
B 1
А 1
5
D
С
4
А
В
3
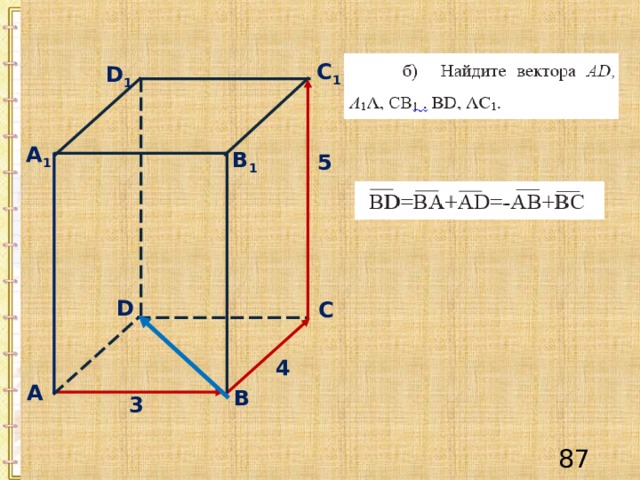
С 1
D 1
А 1
B 1
5
D
С
4
А
В
3
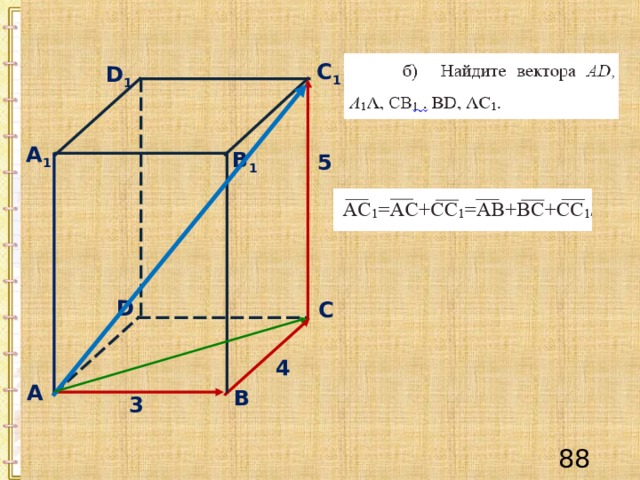
С 1
D 1
А 1
B 1
5
D
С
4
А
В
3
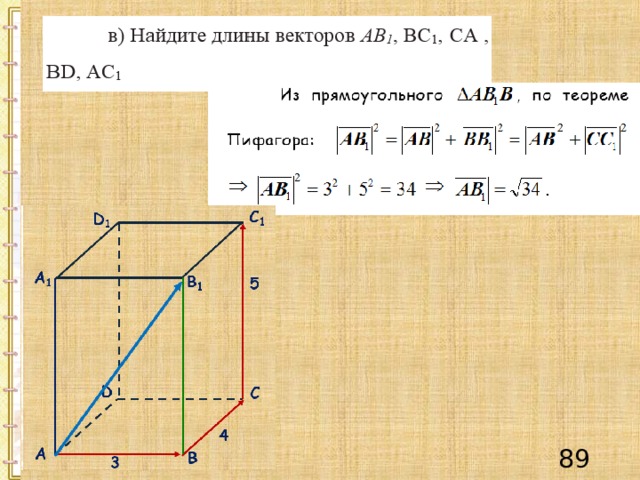


 Получите свидетельство
Получите свидетельство Вход
Вход












 Тема 5.2.9 Координатный метод решения задач на многогранники (8.71 MB)
Тема 5.2.9 Координатный метод решения задач на многогранники (8.71 MB)
 0
0 165
165 32
32 Нравится
0
Нравится
0


