Изучение метода координат является неотъемлемой частью школьного курса геометрии. Этот метод является достаточно мощным аппаратом для доказательства теорем и решения многих геометрических задач, в том числе и задач ЕГЭ. Его преимущество перед другими методами решения геометрических задач вполне очевидно.
Во-первых, применение метода координат зачастую не требует от учеников построения довольно сложных чертежей, тем самым избавляет их от необходимости прибегать к наглядному представлению сложных пространственных изображений.
Во-вторых, при грамотном применении этот метод позволяет решить геометрическую задачу с помощью лишь алгебраических вычислений.
В-третьих, применение метода координат во многом алгоритмизировано, что в большинстве случаев в значительной степени упрощает поиск решения задачи.
Наконец, в-четвертых, метод координат демонстрирует тесную связь алгебры с геометрией, реализуя тем самым межпредметные связи.
В стереометрических задачах наиболее трудными являются задачи на вычисление двугранных углов, углов между скрещивающимися прямыми и пересекающимися плоскостями, а также на вычисление расстояний от точки до плоскости, между скрещивающимися прямыми, прямой и параллельной ей плоскостью и параллельными плоскостями. В данной статье будут рассмотрены примеры решения таких задач, встречающихся на ЕГЭ, с применением метода координат.
Пример 1. В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые ребра равны 3. На ребре AA1 отмечена точка E так, что AE : EA1 = 1 : 2. Найдите угол между плоскостями ABC и BED1.
Если в задаче приходится иметь дело с прямоугольным параллелепипедом, правильной четырехугольной призмой или даже кубом – значит, метод координат как нельзя лучше подходит для решения, поскольку перечисленные многогранники отлично вписываются в прямоугольную систему координат.
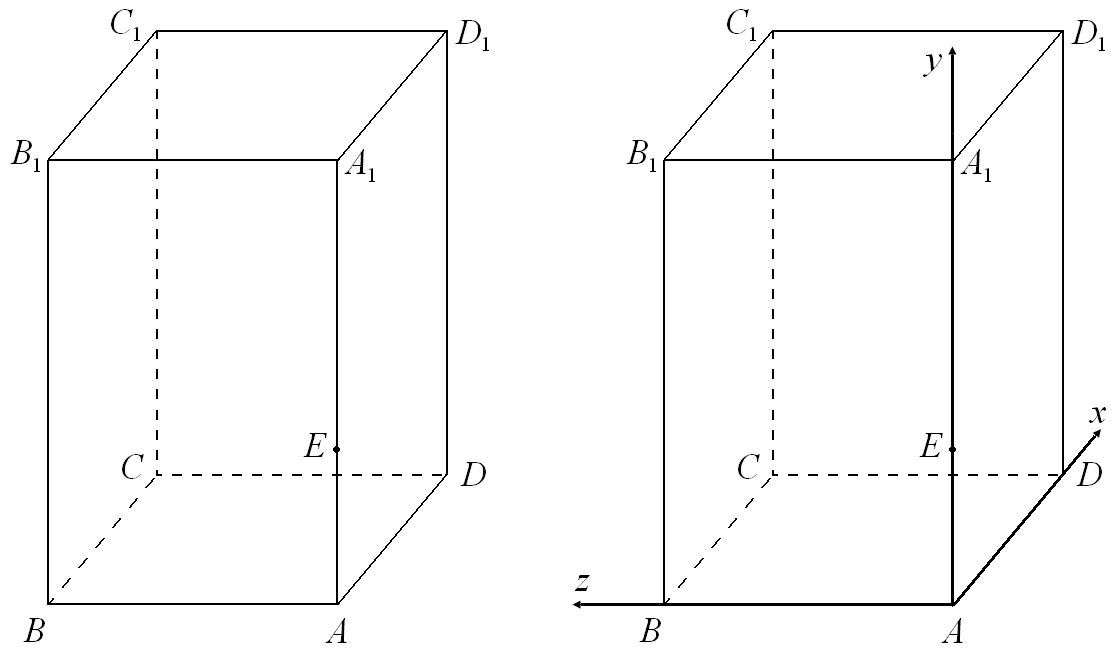
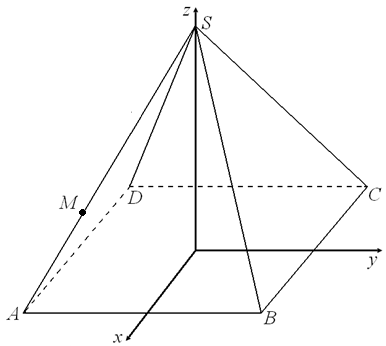
Для решения задачи сделаем чертеж, но отметим, что он выполняется исключительно для того, чтобы правильно выбрать систему координат и задать уравнения соответствующих плоскостей. Непосредственно для решения задачи чертеж использоваться не будет. Заметим еще, что при наличии определенного уровня навыков решения подобных задач ученики могут и вовсе обойтись без чертежа.

Наиболее удобно в данной задаче представляется в качестве начала координат выбрать точку A, а координатные оси направить вдоль ребер AD, AB и AA1. Нетрудно видеть, что AE = 1, EA1 = 2. При таком выборе системы координат запишем координаты точек, через которые будут проходить данные в задаче плоскости: A(0;0;0) , B(0;0;2) , C(2;0;2) , E(0;1;0) , D1(2;3;0) .
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



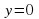 ,
, 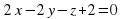 .
.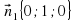 и
и 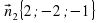 перпендикулярны плоскостям ABC и BED1 соответственно. Значит, угол
перпендикулярны плоскостям ABC и BED1 соответственно. Значит, угол  между плоскостями численно равен углу между этими векторами, который найдем с помощью скалярного произведения:
между плоскостями численно равен углу между этими векторами, который найдем с помощью скалярного произведения: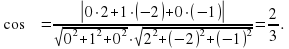
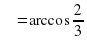 .
.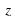 направить перпендикулярно основанию, а оси
направить перпендикулярно основанию, а оси 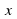 и
и 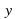 – параллельно сторонам основания.
– параллельно сторонам основания.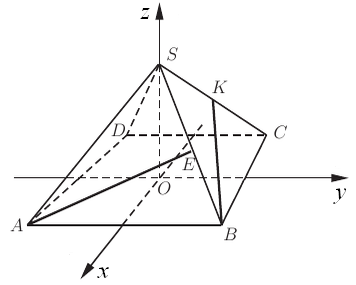
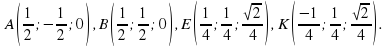
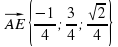 и
и 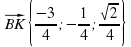 , косинус которого найдем через скалярное произведение:
, косинус которого найдем через скалярное произведение: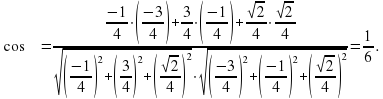
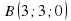 ,
, 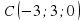 ,
, 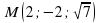 ,
, 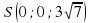 . Тогда уравнение плоскости BCM будет иметь вид
. Тогда уравнение плоскости BCM будет иметь вид 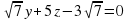 .
.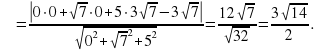









 Материал по математике "Метод координат при решении задач стереометрии" (89.13 КB)
Материал по математике "Метод координат при решении задач стереометрии" (89.13 КB)
 0
0 559
559 12
12 Нравится
0
Нравится
0


