Муниципальное бюджетное общеобразовательное учреждение
«Гатчинская средняя общеобразовательная школа №7»
«УТВЕРЖДАЮ»:
Директор______________/ Соловьев И.Ю./
Приказ № 78 от «29» августа 2014 г.
Рабочая программа
по учебному предмету
«ГЕОМЕТРИЯ»
для базового уровня класс 7 - 9
Рабочая программа составлена на основе Примерной программы среднего общего образования по геометрии (авт. Л.С.Атанасян и др. (М.: Просвещение.2013г.)) в соответствии с требованиями Федерального государственного образовательного стандарта среднего общего образования.
Разработчик программы:
Алексеева Светлана Ивановна
учитель математики, первая квалификационная категория
| «РАССМОТРЕНА»:
на заседании ШМО Протокол № 1 от «28» августа2014г. Руководитель _____________ /Васильева В. К./ (подпись, расшифровка) | «СОГЛАСОВАНА»:
Зам. директора по УВР ___________ /Иванова Г.А./ (подпись, расшифровка) «29» августа 20 14г. |
Пояснительная записка
Рабочая программа по геометрии составлена на основе федерального государственного стандарта основного общего образования. Данная рабочая программа полностью отражает базовый уровень подготовки школьников по разделам программы. Она конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Данная рабочая программа ориентирована на учащихся 7 – 9 классов, изучающих предмет на базовом уровне и реализуется на основе следующих документов:
Закона «Об образовании» от 26.12.2012г. N 273 -ФЗ
Федерального государственного образовательного стандарта (ФГОСа) основного общего образования, утверждённого Приказом Министерства образования и науки РФ от 17.12. 2010г. № 1897
Программы для общеобразовательных учреждений: сборник «Программы для общеобразовательных учреждений, геометрия 7- 9 классы», составитель Т. А. Бурмистрова, Москва, издательство « Просвещение», 2009 год
Приказа Министерства образования и науки РФ от 31.03.2014г. № 253 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию
Санитарно – эпидемиологических правил и нормативов СанПин 2.4.2.2821-10 (утверждены постановлением Главного государственного санитарного врача РФ от 29.12.2010 г. № 189)
Образовательная программа основного общего образования МБОУ «Гатчинская СОШ №7»
Рабочая программа включает в себя следующие разделы:
1) пояснительная записка, в которой конкретизируются общие цели основного общего образования с учѐтом специфики учебного предмета;
2) общая характеристика учебного предмета, курса;
3) описание места учебного предмета, курса в учебном плане;
4) личностные, метапредметные и предметные результаты освоения конкретного учебного предмета;
5) содержание учебного предмета, курса;
6) тематическое планирование (последовательность изучения разделов и тем) с распределением учебных часов;
7) описание учебно-методического и материально-технического обеспечения образовательного процесса;
8) планируемые результаты изучения учебного предмета, курса.
В рабочей программе учтены идеи и положения Концепции духовно-нравственного развития и воспитания личности гражданина России, Программы развития и формирования универсальных учебных действий, которые обеспечивают формирование российской гражданской идентичности, овладения ключевыми компетенциями, составляющими основу для саморазвития и непрерывного образования, целостность общекультурного, личностного и познавательного развития учащихся, и коммуникативных качеств личности.
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Общая характеристика курса
Геометрия – один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В курсе условно можно выделить следующие содержательные линии: «Наглядная геометрия», «Геометрические фигуры», «Измерение геометрических величин», «Координаты», «Векторы», «Логика и множества», «Геометрия в историческом развитии».
Материал раздела «Наглядная геометрия» содержит элементы наглядной стереометрии и способствует развитию пространственных представлений учащихся при изучении планиметрии.
Содержание разделов «Геометрические фигуры» и «Измерение геометрических величин» нацелено на получение конкретных знаний о геометрической фигуре как важнейшей математической модели для описания окружающего мира.
Систематическое изучение свойств геометрических фигур позволит развить логическое мышление и показать применение этих свойств при решении задач вычислительного и конструктивного характера, а также при решении практических задач.
Материал, относящийся к содержательным линиям «Координаты» и «Векторы», в значительной степени несёт
в себе межпредметные знания, которые находят применение как в различных математических дисциплинах, так и в смежных предметах (физике).
Особенностью линии «Логика и множества» является то, что представленный здесь материал преимущественно изучается при рассмотрении различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.
Линия «Геометрия в историческом развитии» предназначена для формирования представлений о геометрии
как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения.
В ходе освоения содержания курса геометрии учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике;
сформировать практические навыки выполнения устных, письменных инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком геометрии; выработать формально-оперативные геометрические умения и научиться применять их к решению математических и нематематических задач;
развить пространственные представления и изобразительные умения;
освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления об особенностях выводов и прогнозов; развить логическое мышление и речь – умения логически обосновывать суждения; проводить несложные систематизации;
приводить примеры и контрпримеры; использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В ходе преподавания геометрии в 7-9 классах, работы над формированием у учащихся универсальных учебных действий следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Место предмета в базисном учебном плане
В соответствии с Федеральным государственным образовательным стандартом, учебным планом МБОУ «Гатчинская СОШ №7» на этапе основного общего образования предусмотрено по 68 учебных часов для обязательного изучения курса «Геометрия» в 7-9 классах из расчета 2 часа в неделю, всего 204 часа.
Цели и задачи обучения
Обучение математике в основной школе направлено на достижение следующих целей:
1. В направлении личностного развития:
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей.
2. В метапредметном направлении:
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.
3. В предметном направлении:
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для развития математических способностей и механизмов мышления, формируемых математической деятельностью.
В ходе изучения материала предполагается закрепление и отработка основных умений и навыков, их совершенствование, а также систематизация полученных ранее знаний. Таким образом, решаются следующие задачи:
введение терминологии и отработка умения её грамотного использования;
развитие навыков изображения планиметрических фигур и простейших геометрических конфигураций;
совершенствование навыков применения свойств геометрических фигур как опоры при решении задач;
формирование умения доказывать равенство данных треугольников;
отработка навыков решения простейших задач на построение с помощью циркуля и линейки;
формирование умения доказывать параллельность прямых, используя соответствующие признаки, находить равные углы при параллельных прямых, что находит широкое применение в дальнейшем курсе геометрии;
расширение знаний учащихся о треугольниках.
Личностные, метапредметные и предметные результаты освоения учебного предмета
Изучение математики в основной школе даёт возможность обучающимся достичь следующих результатов:
1. В направлении личностного развития:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
2. В метапредметном направлении:
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов.
3. В предметном направлении:
предметным результатом изучения курса является сформированность следующих умений:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов); для углов от 0˚ до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и вычислять площади треугольников, длины ломаных, дуг окружности; находить площади основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Результаты изучения предмета влияют на итоговые результаты обучения, которых должны достичь все учащиеся, оканчивающие 7-9 классы, что является обязательным условием положительной аттестации ученика за курс 7-9 классов.
Содержание учебного предмета
7 класс
Начальные понятия и теоремы геометрии.
Возникновение геометрии из практики.
Геометрические фигуры и тела. Равенство в геометрии.
Точка, прямая и плоскость.
Понятие о геометрическом месте точек.
Расстояние. Отрезок, луч. Ломаная.
Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла и ее свойства.
Параллельные и пересекающиеся прямые. Перпендикулярность прямых. Теоремы о параллельности и перпендикулярности прямых. Свойство серединного перпендикуляра к отрезку. Перпендикуляр и наклонная к прямой.
Многоугольники.
Окружность и круг.
Треугольники. Прямоугольные, остроугольные и тупоугольные треугольники. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника.
Признаки равенства треугольников. Неравенство треугольника. Сумма углов треугольника. Внешние углы треугольника. Зависимость между величинами сторон и углов треугольника.
Измерение геометрических величин. Длина отрезка. Длина ломаной, периметр многоугольника.
Расстояние от точки до прямой. Расстояние между параллельными прямыми. Длина окружности, число ; длина дуги. Величина угла. Градусная мера угла.
Построения с помощью циркуля и линейки.
Основные задачи на построение: деление отрезка пополам, построение треугольника по трем сторонам, построение перпендикуляра к прямой, построение биссектрисы.
Конкретно по главам.
1.Начальные геометрические сведения (11 часов)
Раздел математики. Сквозная линия.
Обязательный минимум содержания образовательной области математика
Возникновение геометрии из практики.
Начальные понятия и теоремы геометрии
Геометрические фигуры и тела. Равенство в геометрии.
Точка, прямая и плоскость.
Понятие о геометрическом месте точек.
Расстояние. Отрезок, луч. Ломаная.
Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла и ее свойства.
Перпендикулярность прямых
Основная цель - систематизировать знания учащихся о взаимном расположении точек и прямых; уметь изображать, обозначать отрезки, лучи, углы, а также сравнивать их и измерять; строить смежные, вертикальные углы и перпендикулярные прямые.
2.Треугольники(18 часов)
Раздел математики. Сквозная линия.
Обязательный минимум содержания образовательной области математика
Треугольник.
Свойство серединного перпендикуляра к отрезку.
Перпендикуляр и наклонная к прямой.
Прямоугольные, остроугольные и тупоугольные треугольники.
Высота, медиана, биссектриса, средняя линия треугольника.
Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника.
Признаки равенства треугольников.
Основные задачи на построение: деление отрезка пополам, построение треугольника по трем сторонам, построение перпендикуляра к прямой, построение биссектрисы.
Основная цель – научиться применять признаки равенства треугольников, свойства равнобедренного и равностороннего треугольников при решении задач; решать основные задачи на построение с помощью циркуля и линейки.
3. Параллельные прямые (13 часов)
Раздел математики. Сквозная линия.
Обязательный минимум содержания образовательной области математика
Параллельные и пересекающиеся прямые.
Теоремы о параллельности прямых.
Свойства параллельных прямых
Основная цель - понимать, какие отрезки и лучи называются параллельными; уметь применять аксиому параллельных прямых и следствия из нее при решении задач.
4. Соотношения между сторонами и углами треугольника (20 часов)
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Неравенство треугольника.
Сумма углов треугольника.
Внешние углы треугольника.
Зависимость между величинами сторон и углов треугольника.
Свойства прямоугольных треугольников.
Признаки равенства прямоугольных треугольников.
Расстояние от точки до прямой.
Расстояние между параллельными прямыми.
Построения с помощью циркуля и линейки. Основные задачи на построение.
Основная цель - уметь решать задачи, используя теоремы о сумме углов треугольника, о соотношениях между сторонами и углами треугольника, о неравенстве треугольника и следствий из них; знать признаки равенства прямоугольных треугольников и уметь их использовать при решении задач; уметь строить треугольник по трем элементам.
Итоговое повторение курса геометрии (6ч)
Основная цель - повторить и обобщить основные темы, изученные за учебный год.
8 класс
Четырёхугольники. Многоугольник, выпуклый многоугольник, четырёхугольник. Сумма углов выпуклого многоугольника. Вписанные и описанные многоугольники. Правильные многоугольники. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция. Осевая и центральная симметрия.
Площадь. Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Подобные треугольники. Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Окружность. Взаимное расположение прямой и окружности. Касательная к окружности, её свойство и признак. Центральный, вписанный углы; величина вписанного угла; взаимное расположение двух окружностей; равенство отрезков касательных, проведённых из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырёхугольники. Вписанные и описанные окружности правильного многоугольника.
Конкретно по главам.
1. Повторение курса геометрии 7 класса (2часа)
2.Четырехугольники (14 часов)
Многоугольник, выпуклый многоугольник, четырёхугольник. Сумма углов выпуклого многоугольника. Вписанные и описанные многоугольники. Правильные многоугольники. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция. Осевая и центральна симметрия.
Основная цель - изучить наиболее важные виды четырехугольников — параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.
3. Площадь (14 часов)
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Основная цель - расширить и углубить полученные в 5—6 классах представления обучающихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии — теорему Пифагора.
4. Подобные треугольники (20 часов)
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Основная цель - ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
5. Окружность и круг (16 часов)
Центр, радиус, диаметр. Дуга, хорда. Сектор, сегмент. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника.
Основная цель - расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить обучающихся с четырьмя замечательными точками треугольника.
6. Повторение. Решение задач (2 час)
При реализации рабочей программы используется дополнительный материал в ознакомительном плане, создавая условия для максимального математического развития учащихся, интересующихся предметом, для совершенствования возможностей и способностей каждого ученика.
Увеличивается число часов на темы «Площадь» и «Подобные треугольники», так как:
вычисление площади многоугольников является составной частью решения задач по теме «Многогранники» в курсе стереометрии;
практические навыки вычисления площадей многоугольников востребованы в ходе решения задач;
понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника используются при решении задач по физике на нахождение работы.
9 класс
Векторы. Метод координат. Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах.
Длина окружности и площадь круга. Правильные многоугольники. Окружности: описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
Движения. Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрия. Параллельный перенос. Поворот. Наложения и движения.
Конкретно по главам.
1. Повторение курса геометрии 8 класса (2часа)
Понятие вектора. Абсолютная величина и направление вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Коллинеарные векторы. Свойство средней линии треугольника. Понятия медианы, биссектрисы и высоты треугольника. Понятия параллелограмма, и трапеции, свойства и признаки параллелограмма, ромба, прямоугольника.
Основная цель – напомнить учащимся сведения, необходимые при изучении геометрии в 9 классе.
2. Векторы (12 часов). Метод координат (10 часов)
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
Основная цель – научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач.
Вектор определяется как направленный отрезок и действия над векторами вводятся так, как это принято в физике, т. е. как действия с направленными отрезками. Основное внимание должно быть уделено выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число).
На примерах показывается, как векторы могут применяться к решению геометрических задач. Демонстрируется эффективность применения формул для координат середины отрезка, расстояния между двумя точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым даётся представление об изучении геометрических фигур с помощью методов алгебры.
Основные требования к учащимся:
В результате изучения раздела учащиеся должны знать формулировки и доказательства леммы о коллинеарных векторах и теоремы о разложении вектора по двум неколлинеарным векторам, правила действий над векторами с заданными координатами; уметь выводить формулы координат вектора через координаты его начала и конца, координат середины отрезка, длины вектора и расстояния между двумя точками, выводить уравнения окружности и прямой, строить окружности и прямые, заданные уравнениями, решать простейшие геометрические задачи.
3. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов(14 часов)
Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов , его свойства и его применение в геометрических задачах.
Основная цель - развить умение учащихся применять тригонометрический аппарат при решении геометрических задач.
Синус и косинус любого угла от 0° до 180° вводятся с помощью единичной полуокружности, доказываются теоремы синусов и косинусов и выводится еще одна формула площади треугольники (половина произведения двух сторон на синус угла между ними). Этот аппарат применяется к решению треугольников.
Скалярное произведение векторов вводится как в физике (произведение для векторов на косинус угла между ними). Рассматриваются свойства скалярного произведения и его применение при решении геометрических задач.
Основное внимание следует уделить выработке прочных навыков в применении тригонометрического аппарата при решении геометрических задач.
Основные требования к учащимся:
В результате изучения раздела учащиеся должны знать как вводится синус, косинус и тангенс для углов от 0 до 180 градусов, формулы для вычисления координат точки, что такое угол между векторами, определение скалярного произведения векторов, выражение скалярного произведения в координатах и его свойства; уметь доказывать основное тригонометрическое тождество, теорему о площади треугольника, теоремы синусов, косинусов, решать простейшие геометрические задачи.
4. Длина окружности и площадь круга (12 часов)
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
Основная цель - расширить знание учащихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.
В начале темы дается определение правильного многоугольника и рассматриваются теоремы об окружностях, описанной около правильного многоугольника и вписанной в него. С помощью описанной окружности решаются задачи о построении правильного шестиугольника и правильного 2n-угольника, если дан правильный n-угольник.
Формулы, выражающие сторону правильного многоугольника и радиус вписанной в него окружности через радиус описанной окружности, используются при выводе формул длины окружности и площади круга. Вывод опирается на интуитивное представление о пределе: при неограниченном увеличении числа сторон правильного многоугольника, вписанного в окружность, его периметр стремится к длине этой окружности, а площадь — к площади круга, ограниченного окружностью.
Основные требования к учащимся:
В результате изучения раздела учащиеся должны знать определение правильного многоугольника; формулы для вычисления угла, площади ,стороны правильного многоугольника и радиуса вписанной в него окружности; формулы длины окружности и дуги окружности; формулы площади круга и кругового сектора; уметь доказывать теоремы об окружности, описанной около правильного многоугольника, и окружности, вписанной в правильный многоугольник; применять формулы при решении простейших геометрических задач.
5. Движения (10часов)
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения. Беседа об аксиомах геометрии.
Основная цель - познакомить обучающихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений; дать более глубокое представление о системе аксиом планиметрии и аксиоматическом методе.
Движение плоскости вводится как отображение плоскости на себя, сохраняющее расстояние между точками. При рассмотрении видов движении основное внимание уделяется построению образов точек, прямых, отрезков, треугольников при осевой и центральной симметриях, параллельном переносе, повороте. На эффектных примерах показывается применение движений при решении геометрических задач.
Понятие наложения относится в данном курсе к числу основных понятий. Доказывается, что понятия наложения и движения являются эквивалентными: любое наложение является движением плоскости и обратно. Изучение доказательства не является обязательным, однако следует рассмотреть связь понятий наложения и движения.
Основные требования к учащимся:
В результате изучения раздела учащиеся должны знать, что такое отображение плоскости на себя; определение движения плоскости; понимать, что такое параллельный перенос, поворот; уметь доказывать, что осевая и центральная симметрии являются движениями ,что при движении отрезок отображается на отрезок, треугольник - на равный ему треугольник; доказывать, что параллельный перенос и поворот являются движениями плоскости; решать простейшие геометрические задачи.
6. Повторение. Решение задач (8 часов)
Основная цель - повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 7-9 класса.
Внесены элементы дополнительного содержания:
при повторении темы «Треугольники»: формулы, выражающие площадь треугольника через периметр и радиус вписанной окружности, через стороны треугольника и радиус описанной окружности, формула Герона;
при повторении темы «Четырёхугольники»: площадь четырёхугольника;
при изучении раздела «Правильные многоугольники»: правильные многогранники.
Тематическое планирование (последовательность изучения разделов и
тем) с распределением учебных часов
7 класс
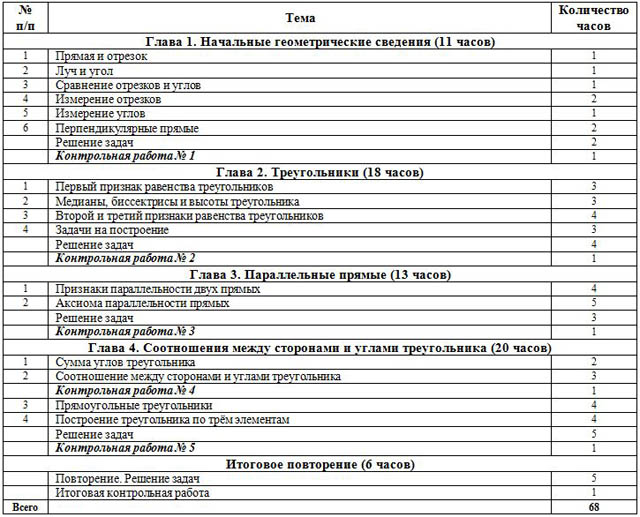
| № п/п | Тема | Количество часов |
| Глава 1. Начальные геометрические сведения (11 часов) |
| 1 | Прямая и отрезок | 1 |
| 2 | Луч и угол | 1 |
| 3 | Сравнение отрезков и углов | 1 |
| 4 | Измерение отрезков | 2 |
| 5 | Измерение углов | 1 |
| 6 | Перпендикулярные прямые | 2 |
|
| Решение задач | 2 |
|
| Контрольная работа № 1 | 1 |
| Глава 2. Треугольники (18 часов) |
| 1 | Первый признак равенства треугольников | 3 |
| 2 | Медианы, биссектрисы и высоты треугольника | 3 |
| 3 | Второй и третий признаки равенства треугольников | 4 |
| 4 | Задачи на построение | 3 |
|
| Решение задач | 4 |
|
| Контрольная работа № 2 | 1 |
| Глава 3. Параллельные прямые (13 часов) |
| 1 | Признаки параллельности двух прямых | 4 |
| 2 | Аксиома параллельности прямых | 5 |
|
| Решение задач | 3 |
|
| Контрольная работа № 3 | 1 |
| Глава 4. Соотношения между сторонами и углами треугольника (20 часов) |
| 1 | Сумма углов треугольника | 2 |
| 2 | Соотношение между сторонами и углами треугольника | 3 |
|
| Контрольная работа № 4 | 1 |
| 3 | Прямоугольные треугольники | 4 |
| 4 | Построение треугольника по трём элементам | 4 |
|
| Решение задач | 5 |
|
| Контрольная работа № 5 | 1 |
| Итоговое повторение (6 часов) |
|
| Повторение. Решение задач | 5 |
|
| Итоговая контрольная работа | 1 |
| Всего |
| 68 |
8 класс
| № п/п | Тема | Количество часов |
| Повторение курса геометрии 7 класса (2 часа) |
| Глава 5. Четырёхугольники (14 часов) |
| 1 | Многоугольники | 2 |
| 2 | Параллелограмм и трапеция | 6 |
| 3 | Прямоугольник. Ромб. Квадрат | 4 |
| 4 | Решение задач | 1 |
|
| Контрольная работа № 1 | 1 |
| Глава 6. Площадь (14 часов) |
| 1 | Площадь многоугольника | 2 |
| 2 | Площадь параллелограмма, треугольника и трапеции | 6 |
| 3 | Теорема Пифагора | 3 |
|
| Решение задач | 2 |
|
| Контрольная работа № 2 | 1 |
| Глава 7. Подобные треугольники (20 часов) |
| 1 | Определение подобных треугольников | 2 |
| 2 | Признаки подобия треугольников | 5 |
|
| Контрольная работа № 3 | 1 |
| 3 | Применение подобия к доказательству теорем и решению задач | 7 |
| 4 | Соотношения между сторонами и углами прямоугольного треугольника | 3 |
|
| Решение задач | 1 |
|
| Контрольная работа № 4 | 1 |
| Глава 8. Окружность (16 часов) |
| 1 | Касательная к окружности | 3 |
| 2 | Центральные и вписанные углы | 4 |
| 3 | Четыре замечательные точки окружности | 3 |
| 4 | Вписанная и описанная окружности | 4 |
|
| Решение задач | 1 |
|
| Контрольная работа № 5 | 1 |
| Итоговое повторение (2 часа) |
| Всего |
| 68 |
9 класс
| № п/п | Тема | Количество часов |
| Повторение курса геометрии 8 класса (2 часа) |
| Глава 9. Векторы (12 часов) |
| 1 | Понятие вектора | 2 |
| 2 | Сложение и вычитание векторов | 4 |
| 3 | Умножение вектора на число. Применение векторов в решении задач | 4 |
|
| Решение задач | 1 |
|
| Контрольная работа № 1 | 1 |
| Глава 10. Метод координат (10 часов) |
| 1 | Координаты вектора | 2 |
| 2 | Простейшие задачи в координатах | 3 |
| 3 | Уравнение окружности и прямой | 3 |
|
| Решение задач | 1 |
|
| Контрольная работа № 2 | 1 |
| Глава 11. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов (14 часов) |
| 1 | Синус, косинус, тангенс угла | 3 |
| 2 | Соотношения между сторонами и углами треугольника | 6 |
| 3 | Скалярное произведение векторов | 3 |
|
| Решение задач | 1 |
|
| Контрольная работа № 3 | 1 |
| Глава 12. Длина окружности и площадь круга (12 часов) |
| 1 | Правильные многоугольники | 4 |
| 2 | Длина окружности и площадь круга | 4 |
|
| Решение задач | 3 |
|
| Контрольная работа № 4 | 1 |
| Глава 13. Движения (10 часов) |
| 1 | Понятие движения | 3 |
| 2 | Параллельный перенос и поворот | 3 |
|
| Решение задач | 3 |
|
| Контрольная работа № 5 | 1 |
| Итоговое повторение (8 часа) |
|
| Повторение. Решение задач | 7 |
|
| Итоговая контрольная работа | 1 |
| Всего |
| 68 |
Перечень учебно - методического обеспечения программы
Данная программа ориентирована на использование следующих учебников, учебных и учебно-методических пособий:
Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина Геометрия. 7- 9 классы: Учебник для общеобразовательных учреждений. М.: Просвещение, 2013
Л. С. Атанасян, В. Ф. Бутузов, И. И. Юдина, Ю. А. Глазков Геометрия. 7- 9 классы: Рабочая тетрадь. М.: Просвещение, 2013
Б. Г. Зив, В. М. Мейлер Геометрия. 7-9 класс :Дидактические материалы. М.: Просвещение, 2012
Б. Г. Зив, В. М. Мейлер, А. Г. Баханский Геометрия. 7- 11 классы: Задачи по геометрии. М.: Просвещение, 2012
Л. С. Атанасян, В. Ф. Бутузов, И. И. Юдина, Ю. А. Глазков, В. Б. Некрасов Изучение геометрии в 7- 9 классах: Методическое пособие. М.: Просвещение, 2012
Бурмистрова Т.А. Геометрия. 7- 9 классы: Сборник рабочих программ. М.: Просвещение, 2012
Бутузов В.Ф. Геометрия. 7- 9 классы: Рабочие программы к учебнику Л.С.Атанасяна и др. М.: Просвещение, 2012
Гаврилова Н.Ф. Геометрия. 7-9 класс: Контрольно-измерительные материалы. М.: ВАКО, 2012
Научно-теоретический и методический журнал «Математика в школе»;
Еженедельное учебно-методическое приложение к газете «Первое сентября» Математика;
CD «Уроки геометрии Кирилла и Мефодия 7-9 классы»;
Б. Г. Зив «Задачи к урокам геометрии. 7-11 класс»;
В.И.Жохов, Л.Б.Крайнева «Карточки для проведения контрольных работ. Геометрия 7 класс»;
С.М.Саврасова, Г.А.Ястребинецкий «Упражнения по планиметрии на готовых чертежах»
Иченская М.А. Геометрия. 7- 9 классы: Самостоятельные и контрольные работы. М.: Просвещение, 2012
Мищенко Т.М., Блинков А.Д. Геометрия. 7-9 класс: Тематические тесты. ГИА. М.: Просвещение, 2012.
Ресурсы Интернет:
Министерство образования РФ: www.informika.ru, www.ed.gov.ru, www.edu.ru
Тестирование online: 5-11 классы: www.kokch.kts.ru
Сеть творческих учителей: www.it-n.ru
Мегаэнциклопедия Кирилла и Мефодия: http://www.megabook.ru/, http://www.liveexpert.ru/topic/study/math
Педагогическая мастерская: http://www.teacher.fio.ru
Новые технологии в образовании: http://edu.secna.ru/main/
Интернет-ресурс «Единая коллекция цифровых образовательных ресурсов»: http://school-collection.edu.ru.
Интернет-ресурс «Открытый банк заданий по математике»: http://mathege.ru:8080/or/ege/Main.
Проект Webmath.ru: Решение задач по математике в режиме онлайн / http://webmath.ru
Дневник – ру http://lib.dnevnik.ru
http://www.matematika-na.ru - Решение математических задач 5-6 классы.
http://4-8class-math-forum.ru - Детский Математический Форум для школьников 4 - 8 классов.
http://eidos.ru/ - Дистанционное образование: курсы, олимпиады, конкурсы, проекты, интернет-журнал "Эйдос".
http://kvant.mccme.ru/ - сайт Научно-популярного физико-математического журнала "Квант".
http://zaba.ru - сайт "Математические олимпиады и олимпиадные задачи".
http://comp-science.narod.ru - дидактические материалы по информатике и математике: материалы олимпиад школьников по программированию, подготовка к олимпиадам по программированию, дидактические материалы по алгебре и геометрии (6-9 кл.) в формате LaTeX и др.
http://www.school.mos.ru - сайт поможет школьнику найти необходимую информацию для подготовки к урокам, материал для рефератов и т.д.
http://www.history.ru/freemath.htm - бесплатные обучающие программы по математике для школьников.
http://www.uic.ssu.samara.ru/~nauka - сайт "Путеводитель В МИРЕ НАУКИ для школьников".
http://allbest.ru/mat.htm - Электронные бесплатные библиотеки
http://en.edu.ru/db/sect/3217/3284 - Естественно-научный образовательный портал (учебники, тесты, олимпиады, контрольные)
http://mathem.by.ru/index.html - Математика online
http://refportal.ru/mathemaics/ Рефераты по математике
http://www.otbet.ru/ Делаем уроки вместе!
Планируемые результаты изучения курса «Геометрия» 7-9 классов
1. В направлении личностного развития:
формирование положительного отношения к учению, познавательной деятельности желания приобретать новые знания, умения, совершенствовать имеющиеся;
формирование нравственно-этического оценивания усваиваемого содержания;
формирование желания осознавать свои трудности и стремиться к их преодолению; проявлять способность к самооценке своих действий, поступков;
формирование навыков работы по алгоритму;
формирование навыка осознанного выбора наиболее эффективного способа решения.
2. В метапредметном направлении:
умение при необходимости отстаивать свою точку зрения, аргументируя её, подтверждая фактами;
определение цели учебной деятельности, осуществление поиска её достижения; вносить коррективы и дополнения в составленные планы;
умение передавать основное содержание в сжатом, выборочном или развёрнутом виде;
продуктивно общаться и взаимодействовать с коллегами по совместной деятельности;
анализировать условия и требования задачи; уметь выбирать обобщённые стратегии решения задачи;
проводить анализ способов решения задачи с точки зрения их рациональности и экономичности;
сопоставлять и отбирать информацию, полученную из разных источников (справочники, Интернет и др.);
сличать способ и результат своих действий с заданным эталоном, обнаруживать отклонения и отличия от эталона.
3. В предметном направлении:
7 класс
формулировать определения;
иллюстрировать понятия отрезка, луча; угла, прямого, острого, тупого и развернутого углов;
объяснять, что такое геометрическое место точек, приводить примеры геометрических мест точек;
решать задачи на построение, доказательство и вычисления; выделять в условии задачи условие и заключение; опираясь на условие задачи, проводить необходимые доказательные рассуждения; сопоставлять полученный результат с условием задачи;
формулировать определения прямоугольного, остроугольного, тупоугольного, равнобедренного, равностороннего треугольников; распознавать и изображать их на чертежах;
формулировать определение равных треугольников; формулировать и доказывать теоремы о признаках равенства треугольников;
формулировать определения понятий, связанных с окружностью;
изображать, распознавать и описывать взаимное расположение прямой и окружности, двух окружностей;
решать задачи на построение с помощью циркуля и линейки;
находить условия существования решения, выполнять построение точек, необходимых для построения искомой фигуры; доказывать, что построенная фигура удовлетворяет условиям задачи (определять число решений задачи при каждом возможном выборе данных);
формулировать и объяснять свойства длины, градусной меры угла;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
8 класс
объяснять, какая фигура называется выпуклым многоугольником, называть его элементы, находить периметр многоугольника, находить сумму углов выпуклого многоугольника;
формулировать свойства и признаки параллелограмма и равнобедренной трапеции; применять их при решении задач; делить отрезок на n равных частей с помощью циркуля и линейки и решать задачи на построение;
формулировать свойства и признаки прямоугольника, ромба, квадрата; применять их при решении задач; выполнять построение симметричных точек и фигур относительно прямой и точки; распознавать фигуры, обладающие осевой и центральной симметрией;
формулировать основные свойства площадей, находить площадь прямоугольника, параллелограмма, треугольника и трапеции; использовать теорему об отношении площадей треугольников при решении задач;
применять при решении задач теорему Пифагора и обратную её теорему;
формулировать определения пропорциональных отрезков и подобных треугольников, теорему об отношении площадей подобных треугольников и свойство биссектрисы треугольника; применять их при решении задач;
применять при решении задач признаки подобия треугольников;
формулировать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике; применять их при решении задач, а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение;
формулировать определения синуса, косинуса, тангенса острого угла прямоугольного треугольника; знать значения синуса, косинуса, тангенса для углов 30º, 45º, 60º;
описывать случаи взаимного расположения прямой и окружности, формулировать определение касательной, свойство и признак касательной; применять их при решении задач;
объяснять, какой угол называется центральным углом и какой вписанным, как определяется градусная мера дуги окружности, формулировать теорему о вписанном угле, следствия из неё и теорему о произведении отрезков пересекающихся хорд; применять их при решении задач;
формулировать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, теорему о пересечении высот треугольника; применять их при решении задач;
понимать, какая окружность называется вписанной в многоугольник и какая описанной около многоугольника, формулировать теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника, свойства вписанного и описанного четырёхугольников; применять их при решении задач.
9 класс
формулировать определения вектора и равных векторов; изображать и обозначать векторы, откладывать от данной точки вектор, равный данному;
объяснить, как определяется сумма двух и более векторов; формулировать законы сложения векторов, определение разности двух векторов; понимать, какой вектор называется противоположным данному; строить сумму двух и более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника, строить разность двух данных векторов;
объяснять, какой вектор называется произведением вектора на число; формулировать свойства умножения вектора на число; понимать, какой отрезок называется средней линией трапеции; формулировать теорему о средней линии трапеции;
раскладывать вектор по двум неколлинеарным векторам, применять правила действий над векторами с заданными координатами при решении задач;
выводить формулы координат вектора через координаты его конца и начала, координат середины отрезка, длины вектора и расстояния между двумя точками;
составлять уравнения окружности и прямой; уметь строить окружности и прямые, заданные уравнениями;
объяснять, как вводятся синус, косинус и тангенс углов от 0º до 180º; использовать формулы для вычисления координат точки при решении задач;
использовать теорему о площади треугольника, теоремы синусов и косинусов при решении треугольников;
строить угол между векторами, находить скалярное произведение векторов, формулировать условие перпендикулярности ненулевых векторов, находить скалярное произведение векторов в координатах;
формулировать определение правильного многоугольника; теоремы об окружности, описанной около правильного многоугольника, и окружности, вписанной в правильный многоугольник; использовать формулы для вычисления угла, площади и стороны правильного многоугольника и радиуса вписанной в него окружности при решении задач;
использовать формулы длины окружности и дуги окружности, площади круга и кругового сектора при решении задач;
объяснить, что такое отображение плоскости на себя; формулировать определение движания плоскости; понимать, что осевая и центральная симметрии являются движениями и что при движении отрезок отображается на отрезок, а треугольник – на равный ему треугольник;
объяснить, что такое параллельный перенос и поворот; понимать, что параллельный перенос и поворот являются движениями плоскости;
иметь представления о простейших многогранниках, телах и поверхностях в пространстве; знать формулы для вычисления площадей поверхностей и объёмов тел.
В результате изучения курса геометрии основной школы учащийся должен:
понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь:
пользоваться основными единицами длины, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами;
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов); находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений; записи математических утверждений, доказательств;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, длин, площадей, объемов;
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по геометрии (7-9 класс) (71.73 КB)
Рабочая программа по геометрии (7-9 класс) (71.73 КB)
 0
0 2330
2330 80
80 Нравится
0
Нравится
0


