
Теорема Пифагора
Урок изучения нового материала, учитель Демчук И.В., МБОУ СОШ №36 г. Томск

Цель и задачи урока
Образовательная:
- Обобщение и систематизация знаний по данной теме Развитие умений и навыков применения формул для решения задач
- Обобщение и систематизация знаний по данной теме
- Развитие умений и навыков применения формул для решения задач
Развивающая:
- Формирование и развитие умений анализировать условие задачи, составлять модель решения
- Формирование и развитие умений анализировать условие задачи, составлять модель решения
Воспитательная:
- Развитие творческих способностей учащихся
- Развитие творческих способностей учащихся
Задачи:
- Формирование прочных знаний, необходимых для продолжения образования Активизация познавательной деятельности учащихся через ИКТ – технологии
- Формирование прочных знаний, необходимых для продолжения образования
- Активизация познавательной деятельности учащихся через ИКТ – технологии

Устный опрос
- Какой треугольник называется прямоугольным?
- Как называются стороны прямоугольного треугольника?
- Как найти площадь прямоугольного треугольника?
- сторона квадрата равна aсм. Найдите его площадь
- Сторона квадрата равна a+b см. Найдите его площадь

Практическая работа
- Постройте прямоугольный треугольник по известным катетам : 1группа a=3, b=5; 2группа a=6,b=8; 3группа a=5,b=12
- Найдите длину гипотенузы
- Постройте на сторонах треугольника квадраты с данной стороной
- Найдите площади данных квадратов
- Сделайте вывод о соотношении данных площадей

Вывод
Площадь квадрата , построенного на гипотенузе, равна сумме площадей квадратов, построенных на его катетах

Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы

Доказательство теоремы Пифагора
Достроим треугольник до квадрата
со стороной (a+b).
Площадь каждого треугольника ½ab
Площадь квадрата со стороной c равна с²
Площадь большого квадрата это
4*½ab+ c²
С другой стороны площадь большого квадрата (a+b)²=a²+2ab+b²
Таким образом, a²+2ab+b²=c²+2ab
Следовательно , a²+b²=c²
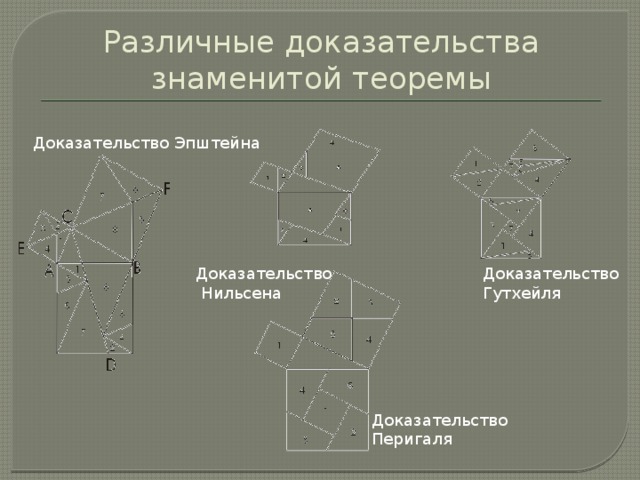
Различные доказательства знаменитой теоремы
Доказательство Эпштейна
Доказательство
Доказательство
Нильсена
Гутхейля
Доказательство
Перигаля

Немного о Пифагоре
Пифагор Самосский жил в vi веке до н.э. в
Древней Греции .В молодости он много
путешествовал по странам, побывал в Египте и Вавилоне, где изучал разные науки. Вернувшись на родину основал философскую школу закрытого типа- пифагорейский союз. Каждый вступавший в него отрекался от имущества и давал клятву хранить в тайне учение основателя. Пифагорейцы занимались математикой, философией, естественными науками. Ими были сделаны важнейшие открытия в арифметике и геометрии. Богатую историю имеет теорема, носящая имя Пифагора. Установлено, что она была известна еще за 1200 лет до Пифагора. Она была известна индусам, китайцам. Встречается и в вавилонских текстах. Пифагор не открыл, а обобщил и доказал свойство о соотношении между катетами и гипотенузой. В настоящее время известно более 200 доказательств теоремы.

Сто быков принес в жертву Пифагор …

Пребудет вечной истина , как скоро
Все познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За свет луча , пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут её почуя , вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать,
От страха, Что вселил в них Пифагор
(А.Шамиссо)

Ослиный мост
Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum «ослиный мост» или elefuga - «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста
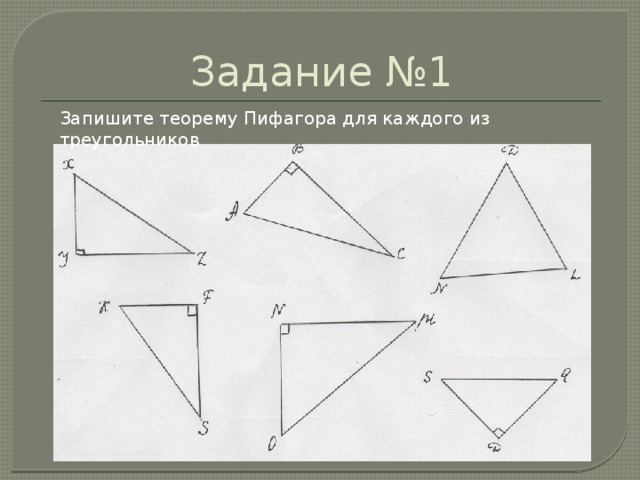
Задание №1
Запишите теорему Пифагора для каждого из треугольников

Задание №2
В прямоугольном треугольнике a и b-катеты, c- гипотенуза.
- Выразить c через a и b
- Выразить a через b и c
- Выразить b через a и с
c
a
b

Задание №3
Вычислите , если возможно
- Сторону АС треугольника АВС
- Сторону MN треугольника MNK
- Диагональ KL прямоугольника KMLN
- Диагональ BD квадрата BCDF
- Сторону АВ ромба ABDE
- Сторону KP треугольника KPR
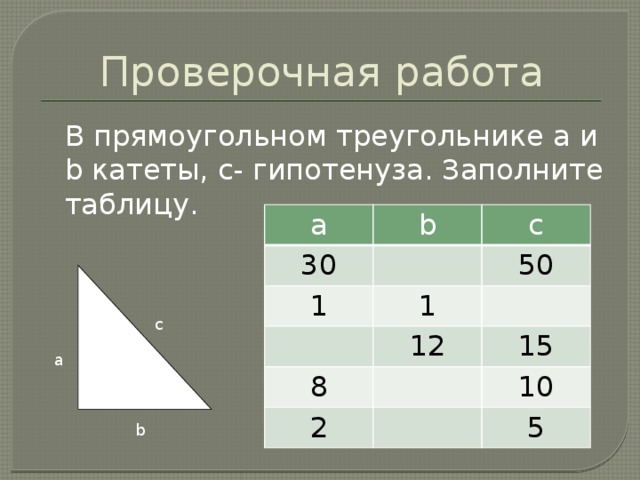
Проверочная работа
В прямоугольном треугольнике a и b катеты, c- гипотенуза. Заполните таблицу.
a
30
b
c
1
50
1
8
12
2
15
10
5
с
a
b
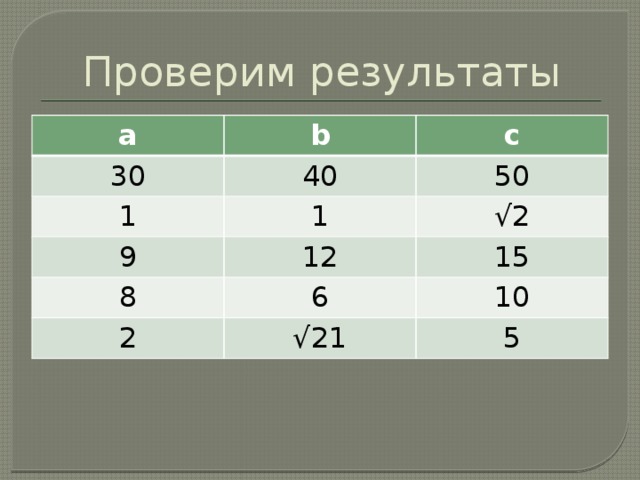
Проверим результаты
a
b
30
c
40
1
1
50
9
8
√ 2
12
6
15
2
10
√ 21
5

Ученические шаржи
- Шаржи из учебника XVI века
Ученический шарж XIX века

Теорема Пифагора
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путем
К результату мы придем.
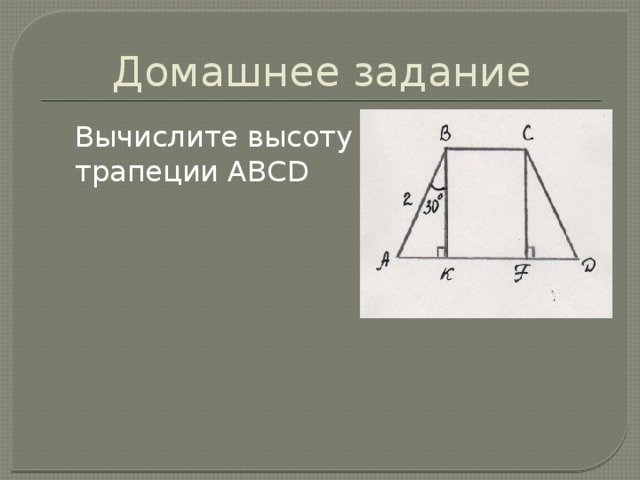
Домашнее задание
Вычислите высоту CF
трапеции ABCD

Рефлексия
Деятельность на уроке
Оценка
Слушал объяснения
Принимал участие в обсуждении
Отвечал на вопросы учителя
Решал самостоятельно
Выполнил домашнее задание
Понял учебный материал


 Получите свидетельство
Получите свидетельство Вход
Вход
































 Теорема Пифагора (8 класс) (0.94 MB)
Теорема Пифагора (8 класс) (0.94 MB)
 0
0 1503
1503 65
65 Нравится
0
Нравится
0







