Сумма углов треугольника
А
С
В

Сумма углов
треугольника равна
180 0 .
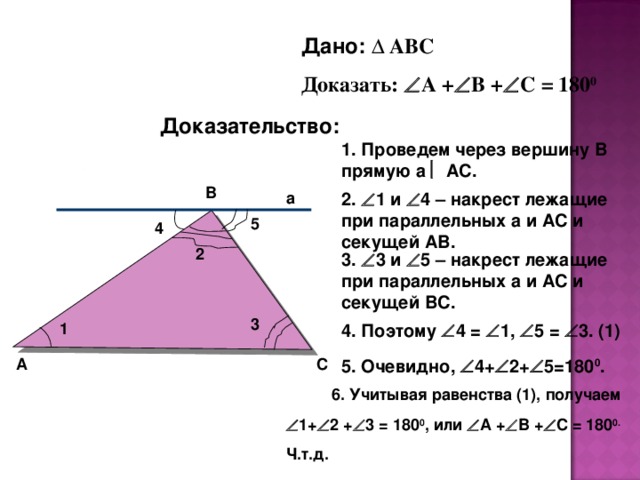
Дано: ∆ АВС
Доказать: А + В + С = 180 0
Доказательство:
1. Проведем через вершину В прямую а АС.
В
2. 1 и 4 – накрест лежащие при параллельных а и АС и секущей АВ.
а
5
4
2
3. 3 и 5 – накрест лежащие при параллельных а и АС и секущей ВС.
3
1
4. Поэтому 4 = 1, 5 = 3. (1)
С
А
5. Очевидно, 4+ 2+ 5=180 0 .
6. Учитывая равенства (1), получаем
1+ 2 + 3 = 180 0 , или А + В + С = 180 0.
Ч.т.д.
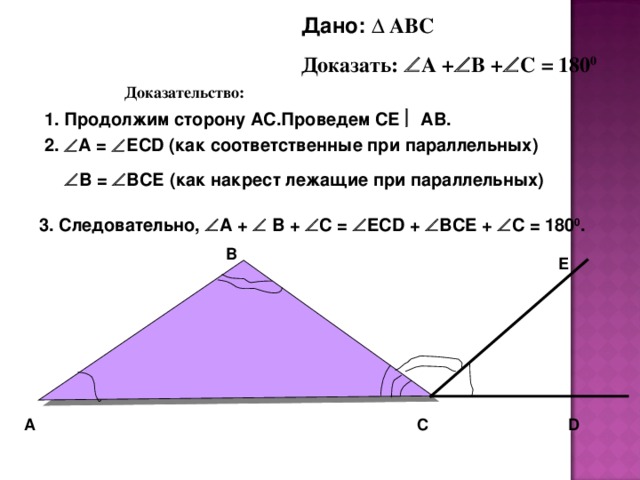
Дано: ∆ АВС
Доказать: А + В + С = 180 0
Доказательство:
Проведем СЕ АВ.
1. Продолжим сторону АС.
2. А = ЕС D (как соответственные при параллельных)
В = ВСЕ (как накрест лежащие при параллельных)
3. Следовательно, А + В + С = ECD + BCE + C = 180 0 .
В
Е
D
С
А
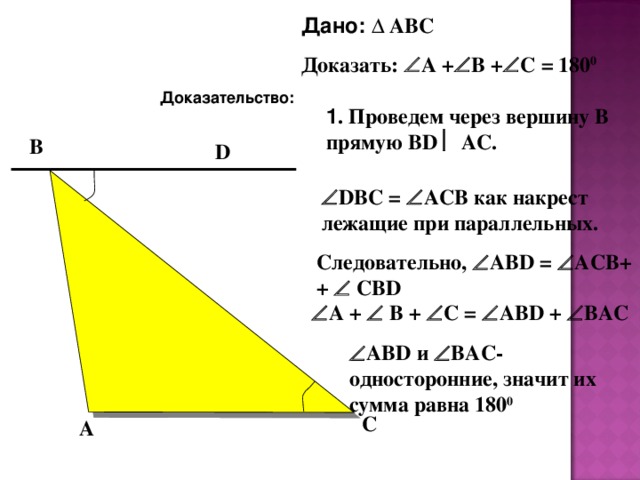
Дано: ∆ АВС
Доказать: А + В + С = 180 0
Доказательство:
1 . Проведем через вершину В прямую BD АС.
В
D
DBC = ACB как накрест лежащие при параллельных.
Следовательно, ABD = АСВ+ + СВ D
А + В + С = ABD + BAC
ABD и BAC - односторонние, значит их сумма равна 180 0
С
А
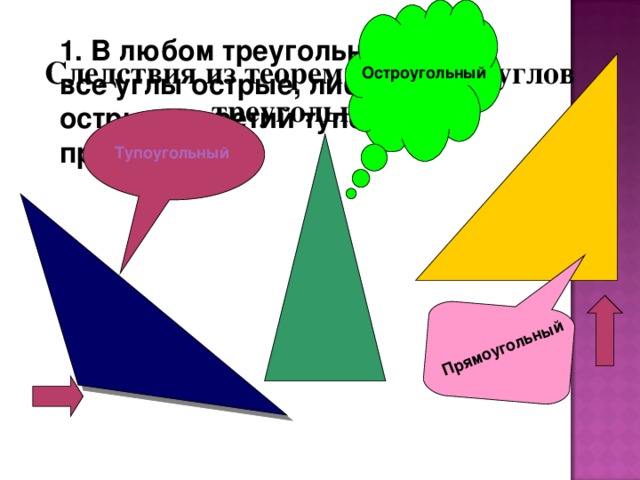
Прямоугольный
1. В любом треугольнике либо все углы острые, либо два острые, а третий тупой или прямой .
Следствия из теоремы о сумме углов треугольника
Остроугольный
Тупоугольный
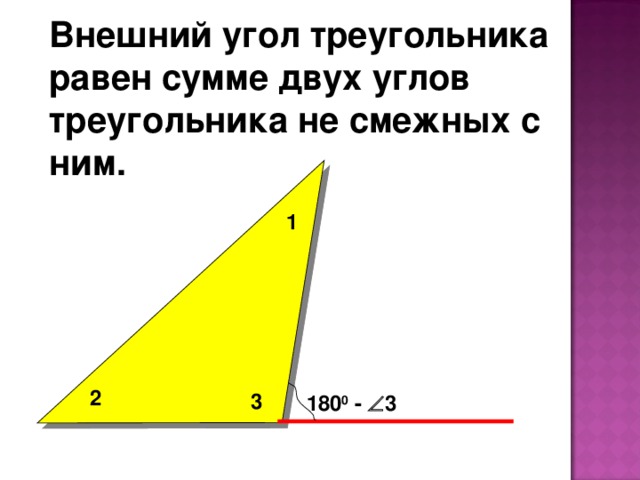
Внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.
1
2
3
180 0 - 3
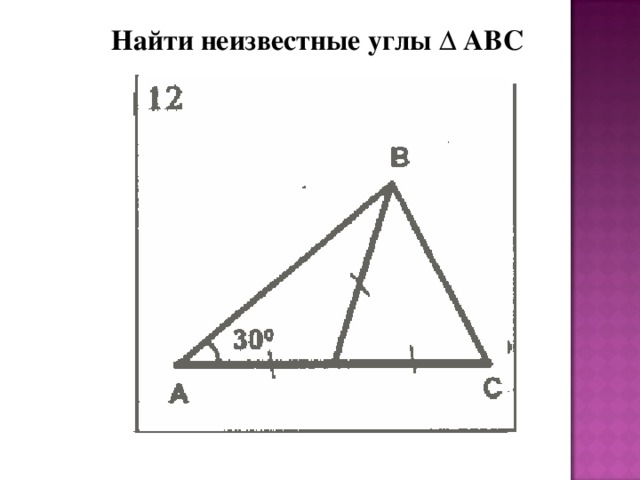
Найти неизвестные углы ∆ АВС

Свойства прямоугольных треугольников
1. Сумма острых углов прямоугольного треугольника равна 90 0 .
=90 0 - α
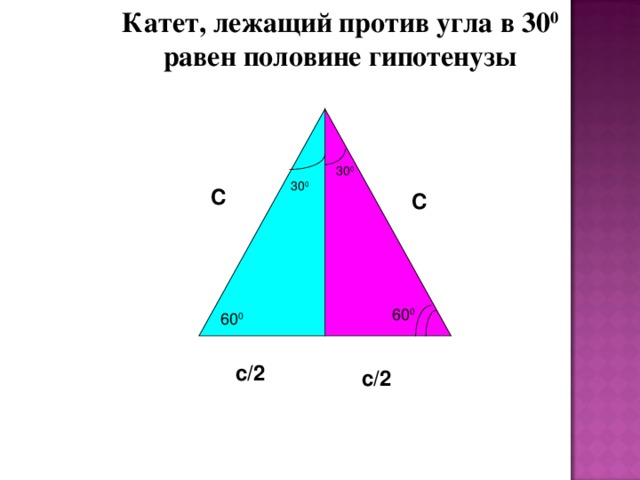
Катет, лежащий против угла в 30 0 равен половине гипотенузы
30 0
30 0
С
С
60 0
60 0
с/2
с/2

 Получите свидетельство
Получите свидетельство Вход
Вход





















 Сумма углов треугольника (1.62 MB)
Сумма углов треугольника (1.62 MB)
 0
0 727
727 173
173 Нравится
0
Нравится
0










