Средняя линия треугольника

Урок геометрии

8 класс

Устная работа

• Дан ∆ АВС, прямая XY параллельна прямой AC .

Доказать, что угол 1 равен углу 2 .

В

Х

Y

1

2

А

С

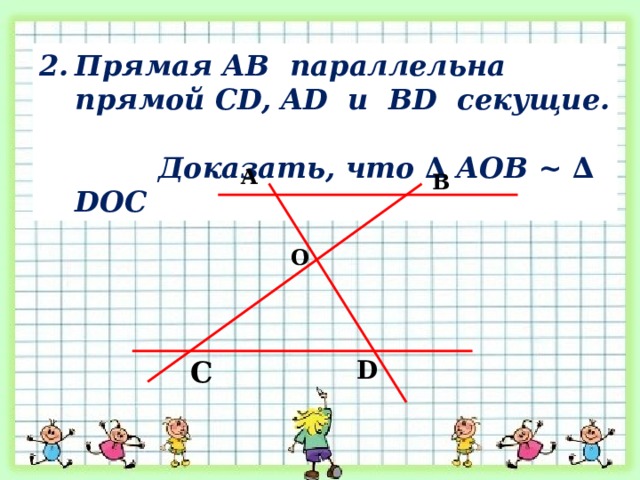
• Прямая АВ параллельна прямой CD, AD и BD секущие.

Доказать, что ∆ АОВ ~ ∆ DO С

A

B

O

C

D

Тема урока :

Средняя линия треугольника

ЦЕЛИ УРОКА:

• дать определение средней линии треугольника,
• доказать теорему о средней линии треугольника,
• решать задачи, используя определение и свойство средней линии.

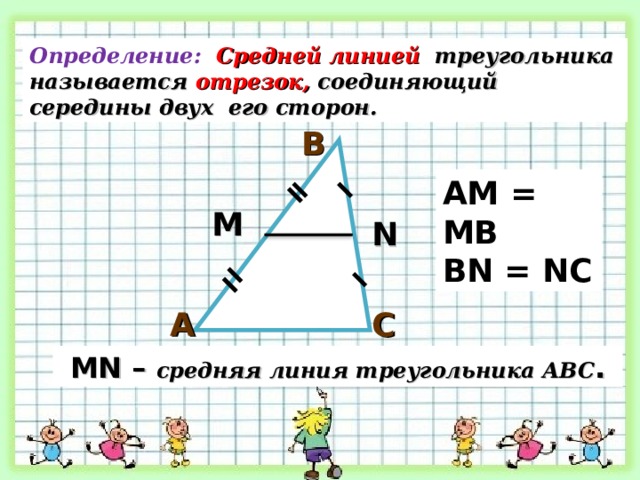
Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

В

AM = MB

BN = NC

М

N

С

А

М N – средняя линия треугольника АВС .

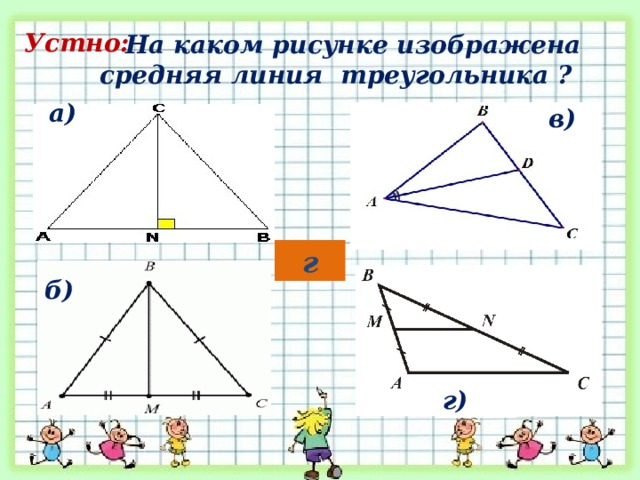
На каком рисунке изображена средняя линия треугольника ?

Устно:

а)

в)

г

б)

г)

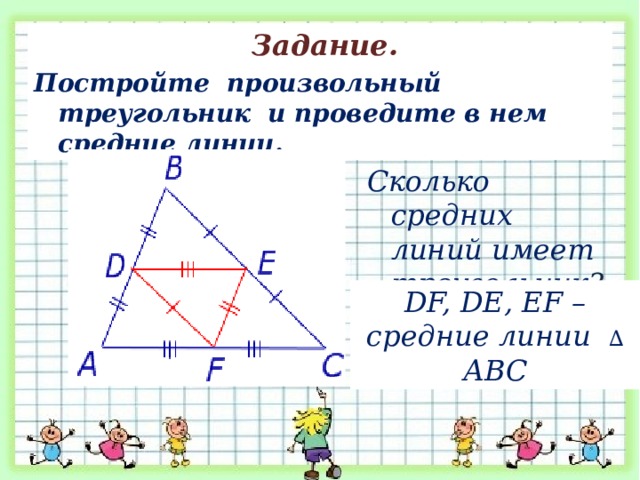
Задание.

Постройте произвольный треугольник и проведите в нем средние линии.

Сколько средних линий имеет треугольник ?

DF, DE, EF –средние линии ∆ АВС

Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Дано: Δ АВС, М N – средняя линия.

Доказать: М N || АС, М N = ½ АС

В

Доказательство:

• Δ АВС ~ Δ ВМ N ,

т.к. ВМ:ВА = В N :ВС=1:2 и угол В – общий.

М

N

2. Угол ВМ N равен углу ВАС,

а они соответственные при прямых М N и АС и секущей АВ. Значит, М N || АС.

С

А

3. Т.к. ВМ:ВА =1:2, то и М N :АС=1:2.

2

Устно:

1. Сколько треугольников вы видите?

∆ ADF, ∆ DBE, ∆ ECF, ∆ DEF, ∆ ABC

2. Есть ли равные треугольники? Почему?

∆ ADF= ∆ DBE= ∆ ECF= ∆ DEF

3. Сколько параллелограммов на рисунке?

ADEF, DBEF, ECFD

Являются ли отрезки EF и CD средними линиями ∆ АВС и ∆ MNK ?

EF является

CD не является

Отрезок MN является средней линией треугольника …

в)

Задача 1 ( ОГЭ)

Средняя линия равностороннего треугольника АВС равна 8 см. Найти периметр этого треугольника.

В

Р ∆ АВС = 48 см

С

А

Задача 2

Дано: S ∆ ABC = 40 см²

Найти: S  MNK

B

N

M

A

C

K

S  MNK = 10 см²

Задача 3 ( ОГЭ)

Найти площадь треугольника, если высота, проведенная к одной из его сторон, равна 10, а средняя линия, параллельная этой стороне, равна 5.

В

К

М

S  АВС = 5 0 см²

А

Н

С

В

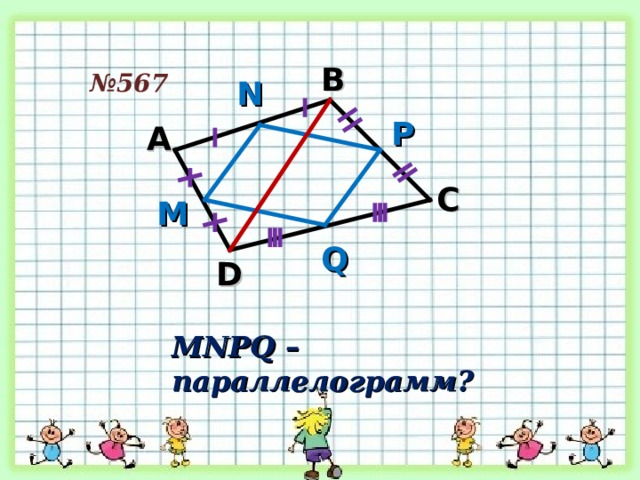
№ 567

N

P

А

С

М

Q

D

MNPQ – параллелограмм?

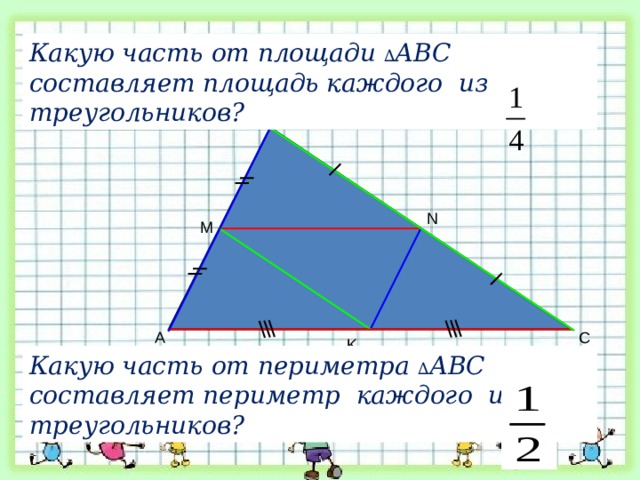
Какую часть от площади ∆ АВС составляет площадь каждого из треугольников?

B

N

M

C

A

K

Какую часть от периметра ∆ АВС составляет периметр каждого из треугольников?

Подведем итог

• Какие новые знания получены на уроке?
• Что называют средней линией треугольника?
• Сформулируйте теорему о средней линии треугольника.

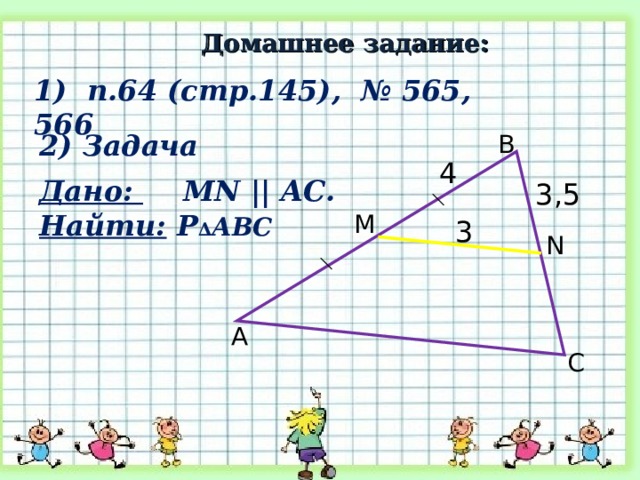
Домашнее задание:

1) п.6 4 (стр.14 5 ), № 565, 566

2) Задача

B

4

Дано: MN || AC .

Найти: Р ∆ АВС

3, 5

M

3

N

A

C

Моё настроение 

Отличное!

Все понятно!

Непонятное!

Есть над чем подумать…