Урок геометрии в 8-м классе на тему "Средняя линия трапеции"
Тип урока: урок открытия нового знания.
Цели урока:
Образовательные:
ввести определение средней линии трапеции;
изучить свойства средней линии трапеции;
формировать умения и навыки применять знания о средней линии трапеции при решении задач.
Развивающие:
развивать геометрическое мышление учащихся при решении геометрических задач, интерес к предмету;
познавательную и творческую деятельность учащихся, математическую речь, память, внимание;
учить учащихся учиться математике, самостоятельно добывать знания.
Воспитательные:
воспитывать у учащихся ответственное отношение к учебному труду, волю;
формировать эмоциональную культуру и культуру общения.
Технологии, применяемые на уроке:
Элементы технологии развития критического мышления.
Технология учебной дискуссии.
Технология проблемного обучения.
Здоровьесберегающие технологии.
Информационно - коммуникативные технологии.
Методы обучения: словесный, наглядный, деятельностный.
Формы обучения: коллективная, индивидуальная.
Оборудование: мультимедиа проектор, экран, карта рефлексии у каждого ученика.
Структура урока:
Мотивация к учебной деятельности – 1 минута.
Проверка домашнего задания, актуализация знаний- 6 минут.
Постановка познавательной задачи – 1 минута.
Открытие новых знаний – 10 минут.
Первичное закрепление новых знаний во внешней речи– 5 минут.
Самостоятельная работа №1 с самопроверкой по эталону-5 минут.
Включение в систему знаний и повторение – 5 минут.
Самостоятельная работа № 2 - 8 минут.
Постановка домашнего задания – 1 минута.
Подведение итогов урока – 2 минуты.
Рефлексия -1 минута.
Ход урока
I.Мотивация к учебной деятельности. (слайд1)
/Цель: включить учащихся в деловой ритм /
Приветствие учеников.
Когда человек не знает, к какой пристани он держит путь, для него ни один ветер не будет попутным.
Сенека
- Ребята, работа предстоит большая и интересная, поэтому, прошу всех слушать меня внимательно, на вопросы мои отвечать, всё подмечать, ничего не забывать.
II. Проверка домашнего задания, актуализация знаний./Цель: проверка и коррекция знаний, умений учащихся по теме «Теорема Фалеса, средняя линия треугольника, трапеция»,актуализация знаний./
Ребята, дома вы должны были к сегодняшнему уроку повторить теоритические вопросы по теме: «Теорема Фалеса, средняя линия треугольника, трапеция» и решить три задачи.
Задачи дом.задания.
1. На стороне угла в 60o отложены от его вершины 3 равных отрезка и через их точки деления проведены параллельные прямые под углом 60o к этой стороне, пересекающие другую сторону угла. Найдите отрезки параллельных прямых, если наименьший из них равен 7.
2. Диагональ квадрата равна 14 см. Середины его сторон последовательно соединены отрезками. Вычислите периметр образовавшегося четырёхугольника.
3. Найдите углы трапеции, если углы, прилежащие к одной из боковых сторон относятся как 7:8, а к другой боковой стороне как 1:5.
К доске вызываются три ученика для краткого изложения домашнего задания.(Чертеж и устное объяснение). Пока ученики готовят чертежи к ответам, провести блиц-опрос теории.
Блиц-опрос теории
1) Сформулируйте теорему Фалеса.
2) О чём говорится в замечании к теореме Фалеса?
3) Кто такой Фалес Милетский?
4) Сформулируйте определение средней линии треугольника.
5) Сколько их?
6) Сформулируйте свойства средней линии треугольника.
7) Что называется трапецией?
8) Назовите виды трапеции.
III. Постановка познавательной задачи /Цель: организация учащихся по принятию познавательной задачи/
-Ребята, как вы думаете, а можно провести среднюю линию в трапеции? Что эта за линия? Что она соединяет? Сколько их можно провести в трапеции? Всё это нам предстоит изучить сегодня на уроке. Поэтому попрошу вас сформулировать тему нашего урока.
«Средняя линия трапеции». (слайд №2).
Откройте тетради, запишите число, тему урока.
IV. «Открытие» новых знаний /Цель: сформулировать определение средней линии трапеции, доказать её свойства, учиться применять их при решении задач/
-Внимание на экран (слайд №3).
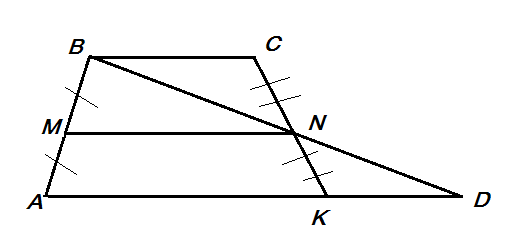
Попытайтесь сформулировать определение средней линии трапеции аналогично определению средней линии треугольника, ведь треугольник можно рассматривать как трапецию, у которой одно основание равно 0, т.е. вершины В и С совпадают. (Учащиеся пытаются сформулировать определение средней линии трапеции). Сколько середин сторон у трапеции? (4) Как их можно соединить? Сколько вариантов соединения? (3). Какие это варианты соединений? (боковая сторона - боковая сторона, боковая сторона – основание, основание – основание)
На доске:
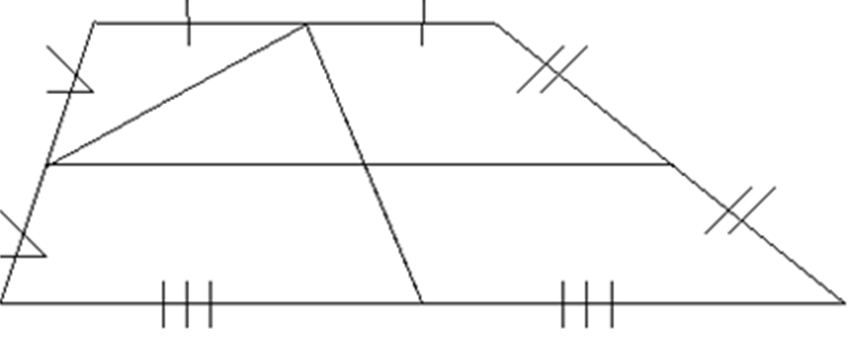
-Как вы думаете, каждый из этих отрезков можно назвать средней линией трапеции?
Какой? Почему? Только один из трёх отрезков называется средней линией трапеции. Это отрезок МК, соединяющий середины боковых сторон трапеции. Так как только этот отрезок, мы замечаем, параллелен основаниям трапеции, точно так же, как средняя линия треугольника параллельна третьей стороне треугольника. Сформулируйте определение средней линии трапеции с опорой на выше изложенное.
Откройте учебник на странице 75 и прочитайте определение средней линии трапеции.
Сколько средних линий можно провести в трапеции? Только одну.
Задание для пробного действия. (слайд 4 )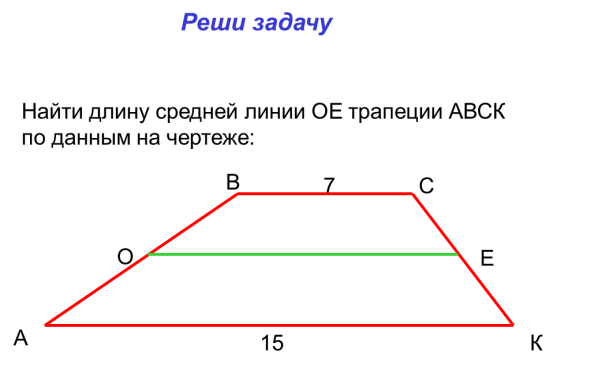
- Обсудите в группах следующий вопрос: является ли это задание пробным. Ответ необходимо обосновать.
Одна из групп предлагает свой вариант ответа и обоснования: это задание пробное, т.к. оно новое, для решения этой задачи недостаточно знаний, полученных на предыдущих уроках. Раньше мы таких заданий не выполняли.
- А теперь каждый задумайтесь, и скажите, какие затруднения у вас могут возникнуть при решении данного задания?
Возможный вариант ответа: я не могу найти среднюю линию трапеции, т.к. не знаю, как связаны между собой основания трапеции и средняя линия.
Выявление места и причины затруднения.
- Посовещайтесь в группах в течение 1 минуты и ответьте на вопросы:
1) какое задание должны были выполнить;
2) чем могли воспользоваться при выполнении задания;
3) в каком месте и почему возникнет затруднение.
Одна из групп озвучивает результат обсуждения, остальные при необходимости уточняют, дополняют.
Возможный вариант ответа: надо было найти среднюю линию трапеции; нет знаний, которыми можно было бы воспользоваться; нет свойства, связывающего среднюю линию и основания трапеции.
Построение проекта выхода из затруднения.
- Посовещайтесь и сформулируйте цель дальнейшей деятельности.
Одна из групп озвучивает результат обсуждения, остальные при необходимости уточняют, дополняют.
Возможный вариант ответа:
Цель: Изучить свойства средней линии трапеции.
(слайд 5)
-Начертите в тетради произвольную трапецию с основаниями 3 см и 5 см. Постройте её среднюю линию и запишите, что отрезок МN - средняя линия трапеции АВСД с основаниями АД и ВС.
Теперь о свойствах средней линии трапеции. С опорой на рисунок уже одно свойство мы заметили. Ещё раз его сформулируйте. (Средняя линия трапеции параллельна её основаниям). Измерьте среднюю линию трапеции, которую вы начертили в тетрадях, установите зависимость между нею и основаниями трапеции. (Средняя линия трапеции равна полусумме оснований трапеции).
Откройте учебник на странице 75,п.59, теорема 6.8 читаем вслух все вместе теорему о свойствах средней линии трапеции. Для доказательства этой теоремы вызвать к доске «продвинутого» ученика.
Теорема. (слайд 6)
Дано: ABCD-трапеция.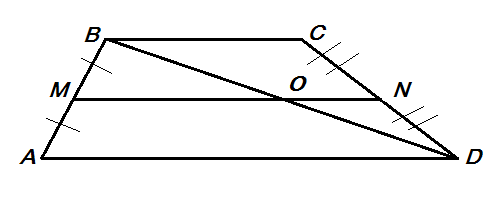
MN-средняя линия трапеции
Доказать: МN II AD, MN II BC, 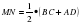
Доказательство: Доказательство ведем аналогично доказательству о средней линии треугольника.
1) Через т.М проведем прямую, параллельную AD. По теореме Фалеса она пересекает отрезки BD и CD в их серединах, т.е.содержит среднюю линию MN.Следовательно, MN IIAD, а значит, и ВС.
2) ВD-диагональ, которая разбивает трапецию ABCD на два треугольника 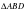 и
и 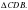 Следовательно, МО-средняя линия
Следовательно, МО-средняя линия 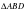 , а NO-средняя линия
, а NO-средняя линия 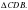 По свойству средней линии треугольника
По свойству средней линии треугольника 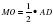 ,
, 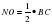 . Так как MN=MO+ОN, то
. Так как MN=MO+ОN, то 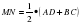 . Что и требовалось доказать.
. Что и требовалось доказать.
Ребята попробуйте придумать другие способы доказательства свойств средней линии трапеции.
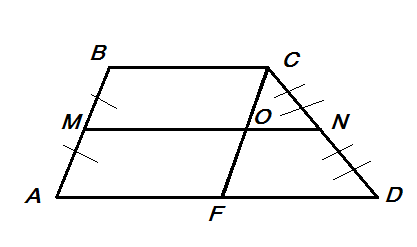
V. Первичное закрепление новых знаний во внешней речи. /Цель: зафиксировать в речи правила, в которых были допущены ошибки/.
Решение задач учащимися под руководством учителя и с его помощью.
1. Вернемся к задаче пробного действия и решим её. (слайд 7)
2. Составьте свою задачу по теме урока и решите её.
3. Как следует изменить основания трапеции а и в, чтобы её средняя линия увеличилась в 2 раза? (надо увеличить каждое основание в 2 раза). (слайд 8)
4. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами, лежащими на прямых, содержащих основания трапеции (например, высоту трапеции).
- Ребята, мы сейчас доказали ещё одно свойство средней линии трапеции. Сформулируем его: «Средняя линия делит пополам любой отрезок с концами, лежащими на прямых, содержащих основания трапеции».
VI.Самостоятельная работа №1 с самопроверкой по эталону. (работа в парах)
/Цель этапа: проверяем способность к выполнению заданий, которые на предыдущей самостоятельной работе вызвали затруднение; сопоставить полученное решение с эталоном для самопроверки./
Вариант1.
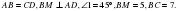
Найти среднюю линию трапеции.
Решение.
Так как 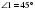 и
и 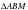 прямоугольный , то этот треугольник равнобедренный. Следовательно,
прямоугольный , то этот треугольник равнобедренный. Следовательно, 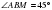 .Значит, АМ=ВМ=5.
.Значит, АМ=ВМ=5.
АD=7+5+5=17.
Средняя линия трапеции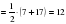 .
.
Ответ:12.
Вариант2.
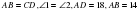
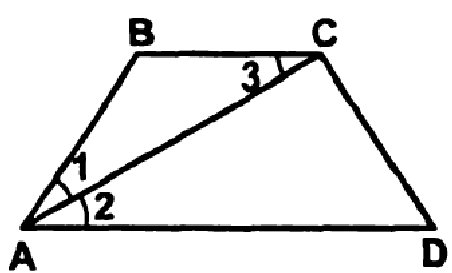
Найти среднюю линию трапеции.
Решение.
Так как 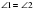 и
и 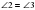 -как внутренние накрест лежащие, то
-как внутренние накрест лежащие, то 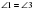 .Значит,
.Значит, 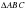 - равнобедренный.Следовательно,АВ=ВС=14.
- равнобедренный.Следовательно,АВ=ВС=14.
Средняя линия трапеции равна
Ответ:16.
На экране вывести задачи и полностью разобрать решение. (слайд 9)
-Назовите, в каких местах и почему возникли затруднения.
Один из учеников озвучивает результаты анализа работы.
VII. Включение в систему знаний и повторение. /Цель этапа: тренировать навыки решения задач/
-Ребята, вашему вниманию предлагается следующая задача, решение которой мы проведем вместе.( (слайд 10).
Задача.

МК-средняя линия трапеции.
Найти МК.
Решение.
Ответ:21.
Провести подробный разбор задачи.
VIII. Самостоятельная работа №2. (слайд 11)
Вариант1.
Вариант2.
МК=
Ответ: 10.
IX. Постановка домашнего задания /Цель: закрепление знаний, умений, полученных на уроке; воспитание ответственного отношения к учебному труду/ (cлайд № 12)
п.59, № 66, № 67, № 68 – стр.83
Вопросы 17-19 (стр.79)
X. Подведение итогов урока (слайд 13 )
Вопросы для закрепления:
- Сформулируйте определение средней линии трапеции.
- Перечислите свойства средней линии трапеции.
Учитель оценивает работу класса и отдельных учеников.
Рефлексия. / Цель: оценить свой вклад в достижении поставленных в начале урока целей, свою активность, эффективность работы класса, увлекательность и полезность выбранных форм работы /.
(слайд 14)
-Ребята, я оценила вашу работу на уроке. А теперь я прошу каждого из вас оценить свою работу на уроке с помощью карточек рефлексии (насколько вы были активны, как точны были ваши ответы, насколько вы постарались, всё ли вам удалось на уроке).
Ребята по цепочке высказываются одним предложением, выбирая начало фразы из рефлексивной карты:
1.На уроке я работал … активно / пассивно
2.Своей работой на уроке я… доволен / не доволен
3.Урок мне показался… коротким / длинным
4.За урок я… не устал / устал
5.Мое настроение… стало лучше / стало хуже
6.Материал урока мне был… понятен / не понятен
полезен / бесполезен
интересен / скучен
легким / трудным
7.Домашнее задание мне кажется… интересно / не интересно
-Урок окончен, спасибо, вам, за урок, ребята .(слайд 15)


 Получите свидетельство
Получите свидетельство Вход
Вход






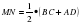
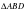 и
и 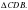 Следовательно, МО-средняя линия
Следовательно, МО-средняя линия 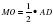 ,
, 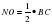 . Так как MN=MO+ОN, то
. Так как MN=MO+ОN, то 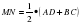 . Что и требовалось доказать.
. Что и требовалось доказать.

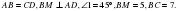

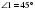 и
и 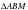 прямоугольный , то этот треугольник равнобедренный. Следовательно,
прямоугольный , то этот треугольник равнобедренный. Следовательно, 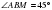 .Значит, АМ=ВМ=5.
.Значит, АМ=ВМ=5.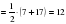 .
.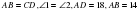

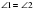 и
и 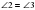 -как внутренние накрест лежащие, то
-как внутренние накрест лежащие, то 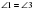 .Значит,
.Значит, 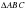 - равнобедренный.Следовательно,АВ=ВС=14.
- равнобедренный.Следовательно,АВ=ВС=14.








 Конспект урока по математике по теме "Средняя линия трапеции" (0.3 MB)
Конспект урока по математике по теме "Средняя линия трапеции" (0.3 MB)
 0
0 2019
2019 412
412 Нравится
0
Нравится
0


