Приём - составная часть или отдельная сторона метода. В процессе обучения приёмы играют важную роль, поскольку они побуждают учащихся к активному участию в освоении учебного материала: постановка вопросов при изложении учебной информации, включение в него отдельных практических упражнений, ситуационных задач, обращение к наглядным и техническим средствам, побуждение к ведению записей. К таким приёмам относят: дидактические игры, логические задачи, упражнения на сравнение и обобщение, самостоятельные работы и т.д.
Также с целью повышения активности учащихся на уроке используются различные методы: проблемные, объяснительно - иллюстративные, логические, метод самостоятельной работы, дидактическая игра, нестандартные виды уроков, тесты, а также различные формы учебной деятельности
Метод и приём могут меняться местами. Но независимо от этого, учитель обязан включить в структуру своего урока тот или иной приём, метод. В результате у учащихся будет формироваться интерес к учебному процессу, повышаться активность, что имеет немаловажное значение для учителя в его работе.
Математические диктанты.
Математические диктанты - хорошо известная форма контроля знаний. Учитель сам или с помощью звукозаписи задаёт вопросы; учащиеся записывают под номерами краткие ответы на них. Однако употребляются они всё же редко.
Первое возражение - не по всякой теме можно и нужно проводить математический диктант.
Второе возражение - учащимся трудно воспринимать на слух. Но если диктанты проводятся часто, то школьники приучаются воспринимать задания на слух. А ценность такого умения неоспорима.
Из того факта, что умение слушать ценно само по себе и его нужно развивать, ещё не следует, что нужно делать это на уроках математики, организуя математические диктанты. Поэтому для успешного усвоения учащимися математики целесообразно проводить диктанты не от случая к случаю, не для того, чтобы разнообразить формы и методы обучения, а систематически.
Работа с тренажерами.
На уроках математики учителя начальных классов часто используют работу с тренажерами. Повышение качества знаний учащихся немыслимо без хорошо отработанных навыков. Тренажер - это тренировочные однотипные упражнения, подобранные по одной теме, и направленные на отработку навыков доведённых до автоматизма. Работу с тренажерами можно включать на различных этапах урока:
*во время устного счета;
*при закреплении нового материала;

*при поведении самостоятельной, проверочной работы;
*при игровых моментах соревновательного характера и т.д.
Учащимся раздаются персональные тетради (тренажеры), через некоторое время (3-5 минут) учитель собирает тетради с ответами, а после урока подсчитывает и фиксирует количество верных ответов в специальной " Таблице успехов”.
Ребятам очень нравится работать в тетрадях-тренажерах и после нескольких работ результат значительно улучшается, так как полученные знания отрабатываются и доводятся до автоматизма.
Схемы - опоры - это, оформленные в виде таблиц, карточек, наборного полотна, чертежа, рисунка, выводы, которые рождаются в момент объяснения.
От традиционной наглядности они отличаются тем, что являются опорами мысли, опорами действия. Школьники строят свой ответ, пользуясь схемой, читают её, работают с ней. По технологии С. Н. Лысенковой ученики избавлены от механического зазубривания правил и формулировок. Они усваивают осмысленно: составляют правило по данной им схеме - опоре, выполняя практическое задание - решение задачи, примера, уравнения.
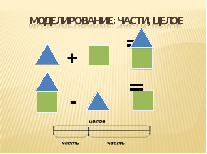
Моделирование - один из наиболее удачных приемов для развития мыслительной деятельности младших школьников. При правильном построении оно достаточно конкретно, легко воспринимается зрительно, полностью отражает внутренние связи и количественные отношения. Любая из моделей и схем проста в исполнении, посильна для ребенка, наглядна, вызывает у детей положительные эмоции. Моделирование способствует развитию логического и абстрактного мышления, готовит ребенка к современной жизни, так как лежит в основе многих компьютерных программ.
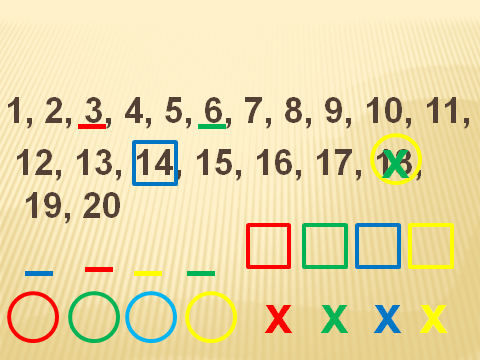
Модель отрезка, на которой изучается взаимосвязь между действиями сложения и вычитания, вводится на первых уроках 1-го класса.
3.1.4 Тесты, как приёмы активизации учащихся при обучении математике
Тестовые задания имеют целью эффективный контроль за знаниями, умениями и навыками учащихся. Они позволяют учителю своевременно обнаружить пробелы в усвоении той или иной темы, чтобы в дальнейшем продумать виды работ для восполнения этих пробелов в знаниях учащихся.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход

















 Современные методы и приемы, используемые на уроках математики в начальной школе (методическая разработка) (1.01 MB)
Современные методы и приемы, используемые на уроках математики в начальной школе (методическая разработка) (1.01 MB)
 0
0 6265
6265 407
407 Нравится
0
Нравится
0






