|
|
Предмет: математика
Тема: Сокращение дробей
Класс: 6
Цель: способствовать созданию условий для самостоятельного открытия учащимися правила сокращения обыкновенных дробей.
Задачи:
Обучающая: подвести учащихся к “открытию” способа сокращения дробей, разработать алгоритм действий и научиться пользоваться им;
Развивающая:развивать логическое мышление, внимательность, самостоятельность, умение рассуждать, делать выводы;
Воспитывающая: продолжить работу по воспитанию любви к предмету, любознательности, чувства сопереживания и уважительного отношения к мнению одноклассников, культуры общения; воспитывать умение сотрудничать в паре.
Тип урока: урок изучения и первичного закрепления новых знаний.
Методы и приемы: словесный, наглядный, исследовательский, проблемно-поисковый.
Формы организации познавательной деятельности: индивидуальная, фронтальная, работа в парах.
Средства обучения: учебник, проектор
| Этапы урока | Организационно-технологический блок | Деятельность учителя | Деятельность учащихся |
| 1.Организационно-психологический настрой детей на урок | Задача: организационная деятельность учащихся. Форма: фронтальная Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку. Прием контроля: наблюдение и самоконтроль. | -Добрый день, ребята! Давайте поприветствуем гостей и одноклассников улыбкой и сохраним хорошее настроение в течение всего урока. Садитесь. -Откройте тетради, запишите число. Классная работа. Оставьте строчку для темы урока. -Пусть наш урок будет интересным и даст нам возможность открыть новые знания. -Сегодня на уроке вы будете работать в парах, самостоятельно и все вместе. | Приветствуют учителя. Настраиваются на работу на уроке. Активизация познавательного внимания, его концентрация на словах учителя. Записывают дату. |
| 2.Актуализация знаний с последующей мотивацией. | Задача: мотивировать учащихся к учебной деятельности. Форма: работа в парах. Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку. Прием контроля: наблюдение и самоконтроль. | -Ребята, на протяжении всей своей жизни мы постоянно сталкиваемся с дробями. Давайте вспомним, что такое дробь и какие действия мы уже умеем выполнять с дробями. Для этого я предлагаю составить кластер: в центре - название - дробь, а по сторонам - умения. -Что такое дробь? -Что показывает дробь? -Что вы знаете о дробях? -Какие действия мы умеем выполнять с дробями? -Сегодня на уроке мы научимся выполнять еще одно действие с обыкновенными дробями и наш кластер умений увеличится. -Ну а теперь проведем небольшое исследование. На каждой парте лежит конверт. Достаньте, пожалуйста из конверта 2 листа с прямоугольниками. 1 вариант - Возьмите лист №1. Раскрасьте 3/6 прямоугольника. 2 вариант - возьмите лист №2 и раскрасьте ½ часть прямоугольника. -Сравните получившиеся части. Что вы заметили? Сделайте вывод? -Мы убедились, что разные дроби могут обозначать одну и ту же часть фигуры. -Откройте учебнике с. 34 прочитайте правило. -Как из дроби ½ получить дробь 3/6? -Что помогает нам утверждать, что эти дроби равны? -Можно ли из дроби 3/6 получить ½? -Если числитель и знаменатель дроби делят на одно и то же число, то в математике говорят, что данную дробь сократили. -Как вы думаете, чему сегодня на уроке мы будем учиться?
| Отвечают на вопросы: Одну долю или несколько равных долей единицы называют дробью или дробным числом. В дроби число, стоящее над чертой, называют числителем дроби, а число, стоящее под чертой, называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделена единица, а числитель дроби показывает, сколько таких частей взято. Работа в паре.
Наблюдают и делают выводы.
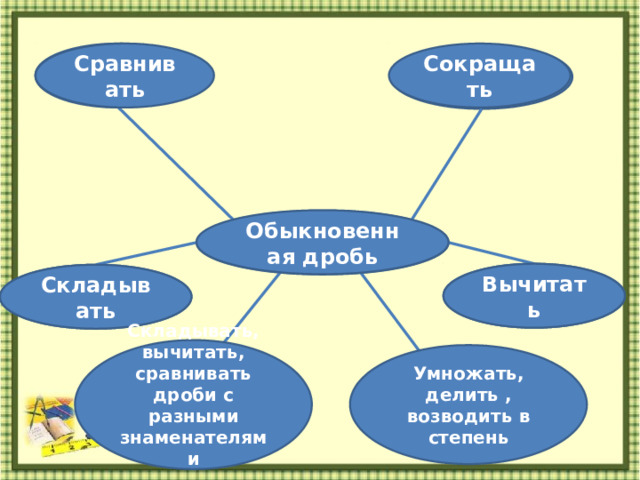
Умножить числитель и знаменатель дроби на 3. Основное свойство дроби. Разделить числитель и знаменатель дроби на 2. Сокращать дроби. |
| 3.Формулировка темы и цели урока. | Задача: мотивировать учащихся на формулировку темы и цели урока. Форма: беседа Результат: сформирована тема и цель урока. | -Попробуйте сформулировать тему нашего урока. -Поставим перед собой цель и задачи.
-Как может звучать правило сокращения дробей? -Где мы можем проверить нашу гипотезу? -Откройте учебник на с. 39 -Прочитаем утверждение, которое здесь записано. -Сравните данное утверждение с тем, которое мы сделали сами. -Что мы не сказали?
-Рассмотрим пример: сократить дробь: 18/24
-На какое число можно сократить дробь, чтобы сразу получилась дробь ¾?
-Что нужно найти, чтобы сократить данную дробь? -Найдём НОД (18,24) = 6
Значит на какое число можно сократить дробь? Разделим числитель и знаменатель на 6.
| В тетради записывают тему урока - сокращение дробей Цель: научиться сокращать дроби. Задачи: 1. познакомиться с правилом сокращения дробей 2. тренироваться сокращать дроби. Пробуют формулировать правило. Предлагают - в учебнике. Сравнивают результаты. Убеждаются в совпадении.
Что дроби надо сокращать на общий делитель числителя и знаменателя. Учащиеся работают в тетради, Один ученик работает у доски.
На 6.
¾
|
| 4.Физминутка |
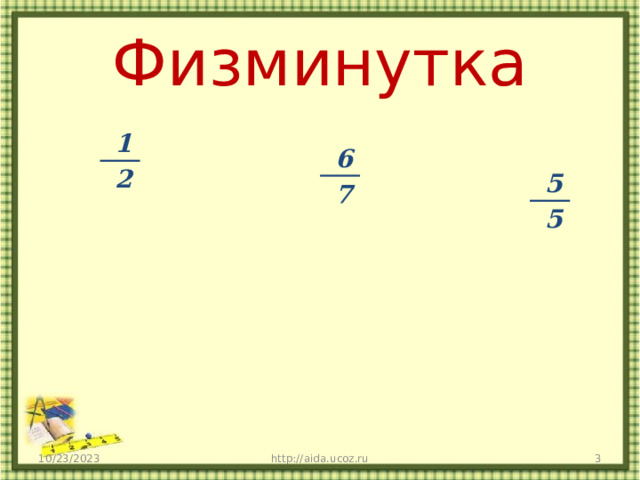
| Встаньте все из-за парт. Сейчас я проверю, насколько вы внимательны, и все ли знаете о дробях. Я говорю утверждение, если вы с ним согласны, вы хлопаете в ладоши над головой 3 раза, если я неправа, вы топаете ногами 1-2. Дробь ½ меньше 1. 6/7 неправильная дробь 5/5 равна единице
Хорошо, молодцы. Тест на пальцах. (На слайде дробь, которую нужно сократить и 4 варианта ответов. Учащиеся показывают пальцами -1,2,3 или 4 –выбирают вариант ответа. Тех кто ответил неверно или подглядывал у других – садить за парту. Выиграют те, которые останутся стоять)
|
|
| 5. Первичное закрепление | Задача: формирование умения по применению на практике правила сокращения дробей Форма: работа у доски и самостоятельно Результат: применяют правило сокращения дробей | -Спасибо, присаживайтесь. -О чем мы сегодня говорим? -Что значит сократить дробь? Итак, мы расмотрели 2 способа – постепенное сокращение дробей и сокращение на НОД -Чтобы выполнить постепенное сокращение данной дроби что нам нужно знать? -Давайте вспомним признаки делимости, которые мы знаем.
А теперь попробуйте сами сократить дробь: 8/16=4/8=2/4=½ (1 человек у доски) 25/75=5/15=1/3(4 чел. У доски) 63/144=(на 9) 7/16 (с обратной стороны) или на 3(21/48, 7/16) 322/84= (на 2) 161/42 (на 7) 23/6
На каком шаге сокращения трудно было определить на что сократить числа? Как рассуждали? -Оцените работу над новым материалом, было ли вам все понятно, или возникли трудности. -Как вам больше понравилось сокращать? Почему? -Что нужно знать для правильного сокращения дроби? Выполним задания на сайте учи.ру вместе. Постарайтесь внимательно определить на какое число можно сократить дробь и правильно выполнить деление. |
О сокращении дробей.
Признаки делимости
На 2, на 5, на 10, на 3, на 9 Работа со слайдом |
| 6.Итог урока, Д/з, рефлексия. |
| Подведем итог -Так какое правило мы сегодня изучали? -Как формулируется правило сокращения дробей? -Давайте вернемся к нашему кластеру о дробях. Какое умение можно добавить? Как вы думаете, все ли мы теперь знаем об обыкновенных дробях? При дальнейшем изучении математики вы научитесь выполнять сложение, вычитание, сравнение обыкновенных дробей с разными знаменателями и, умножать, делить и возводить дроби в степень. Ребята, дома вы продолжите закреплять навык применения правила сокращения дробей. Запишите д/з.
Оцените свою работу на уроке. Ответьте на вопросы, на полях под датой поставьте «+», если вы согласны с утверждением, и поставьте «-», если вы не согласны. Я отвечал (а) на вопросы учителя (поднимал (а) руку) Я понял материал также хорошо, как предполагал Я научился(-лась) сокращать дроби Посчитайте общее кол-во плюсов. Выберите соответствующий смайлик, поднимите над головой. Урок закончен.
|
Записывают д/з п. 8, 9. №268(а,б)№247(а) – на «4» + №271(а,б)- на «5»
Проводят самооценку, рефлексию |
|
| Я отвечал (а) на вопросы учителя (поднимал (а) руку)
|
|
| 2 | Я понял материал также хорошо, как предполагал |
|
| 3 | Я научился(-лась) сокращать дроби
|
|


|
№1

|
№2
| ||||||||
|
№1

| №2
|
2

 Получите свидетельство
Получите свидетельство Вход
Вход




















 Сокращение дробей (194.68 KB)
Сокращение дробей (194.68 KB)
 0
0 751
751 7
7 Нравится
0
Нравится
0


