Сложение и вычитание многочленов

Классная работа.

Сложение и вычитание многочленов.

«Кто с детских лет занимается

математикой, тот развивает

мозг, свою волю, воспитывает

в себе настойчивость и упорство

в достижении цели.»

А. Маркушевич

Цели урока:

• Повторить понятия: одночлен, многочлен, подобные слагаемые.
• Сформулировать правила сложения и вычитания многочленов.
• Научиться складывать и вычитать многочлены.
• Познакомиться с понятием алгебраическая сумма.

Теоретический тест

1. Одночленом называется:

а) произведение чисел.

б) частное чисел и степеней.

в) произведение чисел, переменных и их степеней.

2. Коэффициентом одночлена называют:

а) числовой множитель одночлена.

б) показатель степени одночлена.

в) знак одночлена.

3. Подобными, называются одночлены:

а) у которых одинаковые коэффициенты.

б) у которых одинаковая буквенная часть.

в) имеющие одинаковые знаки.

4. Многочленом называется:

а) сумма или разность нескольких одночленов.

б) произведение нескольких одночленов.

в) частное нескольких одночленов.

Разминка

• Является ли данное выражение одночленом?

2ху; х – у; 2a – 3b; gh + 4; 2m+5n; bk; 3

• Приведите подобные слагаемые

3х+5х; 3р – 7р; 11к + 3к – 7к; 10ху+18ху+14ху; -11ак+8ак+5ак.

3. Решите уравнения

5х+4х=9; 11х-4х=14; 19х-3х+4х=80.

«СЛОЖЕНИЕ»

Чтобы найти сумму нескольких многочленов, надо:

1) каждый многочлен записать в скобках и между скобками поставить знак "+" ;

2) раскрыть скобки ( если перед скобками стоит знак "+", скобки опускают, знаки слагаемых оставляют прежними );

3) привести подобные члены.

Внимательно рассмотри примеры и оформи решения в тетради.

  Пример.

Сложить многочлены 5x 2 + 2x - 1 и

7x + 4.

Решение:

   1) (5x 2 + 2x -1) + (7x + 4);

  Пример.

Сложить многочлены 5x 2 + 2x - 1 и

7x + 4.

Решение:

   1) (5x 2 + 2x -1) + (7x + 4);

   2) 5x 2 + 2x -1 + 7x + 4;

  Пример.

Сложить многочлены 5x 2 + 2x - 1 и

7x + 4.

Решение:

   1) (5x 2 + 2x -1) + (7x + 4);

   2) 5x 2 + 2x -1 + 7x + 4 ;

  Пример.

Сложить многочлены 5x 2 + 2x - 1 и

7x + 4.

Решение:

   1) (5x 2 + 2x -1) + (7x + 4);

   2) 5x 2 + 2x -1 + 7x + 4 ;

   3) 5x 2 + 9x + 3 .

Оформление в тетради:

(5x 2 + 2x -1) + (7x + 4) =

Оформление в тетради:

(5x 2 + 2x -1) + (7x + 4) = 5x 2 + 2x –

1 + 7x + 4

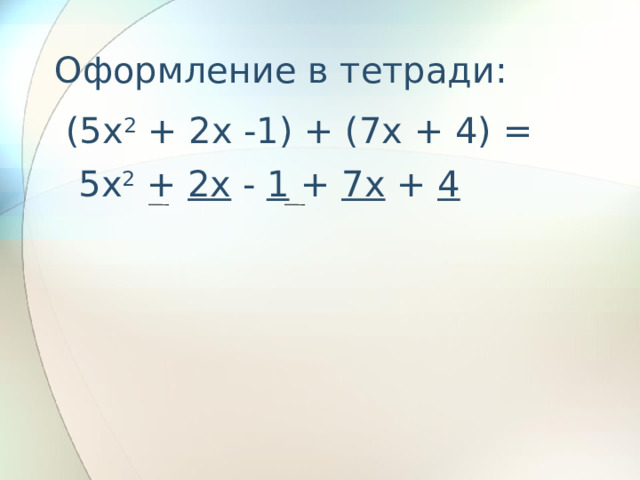
Оформление в тетради:

(5x 2 + 2x -1) + (7x + 4) = 5x 2 + 2x - 1 + 7x + 4

Оформление в тетради:

(5x 2 + 2x -1) + (7x + 4) = 5x 2 + 2x - 1 + 7x + 4 = 5x 2 + 9x + 3.

«ВЫЧИТАНИЕ»

Чтобы вычесть один многочлен из другого надо:

1)записать многочлены в скобках, поставив между скобками знак "-" ;

2) раскрыть скобки (перед скобками стоит знак "-", опуская скобки, знаки слагаемых в них меняют на противоположные);

3) привести подобные члены .

Пример.

Найти разность многочленов 2x 3 + y 3 - 2x + 3y + 7 и 2x 3 – y 3 - 5x + 2y - 4.

        Решение:

1) (2x 3 + y 3 - 2x + 3y + 7) - (2x 3 – y 3 - 5x + 2y - 4);

Найти разность многочленов 2x 3 + y 3 - 2x + 3y + 7 и 2x 3 – y 3 - 5x + 2y - 4.

Решение:

1) (2x 3 + y 3 - 2x + 3y + 7) - (2x 3 – y 3 - 5x + 2y - 4);

2) 2x 3 + y 3 - 2x + 3y + 7- 2x 3 + y 3 + 5x - 2y + 4;

Найти разность многочленов 2x 3 + y 3 - 2x + 3y + 7 и 2x 3 – y 3 - 5x + 2y - 4.

        Решение:

1) (2x 3 + y 3 - 2x + 3y + 7) - (2x 3 – y 3 - 5x + 2y - 4);

2) 2x 3 + y 3 - 2x + 3y + 7 - 2x 3 + y 3 + 5x - 2y + 4;

3)   2y 3 + 3x + y + 11.

    Оформление в тетради:

(2x 3 + y 3 - 2x + 3y + 7) - (2x 3 – y 3 - 5x + 2y - 4) =

Оформление в тетради:

(2x 3 + y 3 - 2x + 3y + 7) - (2x 3 – y 3 - 5x + 2y - 4) = 2x 3 + y 3 - 2x + 3y + 7- 2x 3 + y 3 + 5x - 2y + 4

Оформление в тетради:

(2x 3 + y 3 - 2x + 3y + 7) - (2x 3 – y 3 - 5x + 2y - 4) = 2x 3 + y 3 - 2x + 3y + 7- - 2x 3 + y 3 + 5x - 2y + 4 = 2y 3 + 3x + y + 11

    Сложение и вычитание многочленов выполняется по одному и тому же правилу, т.е. необходимости в различии операции сложения и вычитания нет. Вместо них можно употребить термин "алгебраическая сумма" многочленов.

Общее правило:

    1) составить алгебраическую сумму многочленов;

    2) раскрыть скобки, используя правила знаков "+" и "-";

    3) привести подобные члены .

Давайте, порешаем .

Анализ достигнутых результатов (заполнить таблицу)

Подведем итоги

Цели урока:

• Повторить понятия: одночлен, многочлен, подобные слагаемые .

• Сформулировать правила сложения и вычитания многочленов.

• Научиться складывать и вычитать многочлены.

• Познакомиться с понятием алгебраическая сумма.

Подведем итоги

Цели урока:

• Повторить понятия: одночлен, многочлен, подобные слагаемые .

• Сформулировать правила сложения и вычитания многочленов.

• Научиться складывать и вычитать многочлены.

• Познакомиться с понятием алгебраическая сумма.

+

Подведем итоги

Цели урока:

• Повторить понятия: одночлен, многочлен, подобные слагаемые .

• Сформулировать правила сложения и вычитания многочленов.

• Научиться складывать и вычитать многочлены.

• Познакомиться с понятием алгебраическая сумма.

+

+

Подведем итоги

Цели урока:

• Повторить понятия: одночлен, многочлен, подобные слагаемые .

• Сформулировать правила сложения и вычитания многочленов.

• Научиться складывать и вычитать многочлены.

• Познакомиться с понятием алгебраическая сумма.

+

+

+

Подведем итоги

Цели урока:

• Повторить понятия: одночлен, многочлен, подобные слагаемые .

• Сформулировать правила сложения и вычитания многочленов.

• Научиться складывать и вычитать многочлены.

• Познакомиться с понятием алгебраическая сумма.

+

+

+

+

Молодцы!!!

Спасибо

Вам за

урок!