| Тема урока: Скалярное произведение векторов | Школа: Бауманская | ||||||||||||||||||||||||||||||||||
| Дата: | ФИО учителя:Бибулатова А.Р. | ||||||||||||||||||||||||||||||||||
| КЛАСС: 9 | Количество присутствующих: | Количество отсутствующих:
| |||||||||||||||||||||||||||||||||
| Цели обучения,которые необходимо достичь на данном уроке | Ввести понятие угла между векторами и скалярного произведения векторов, рассмотреть формулу скалярного произведения в координатах | ||||||||||||||||||||||||||||||||||
| Цели обучения | Все учащиеся смогут: | ||||||||||||||||||||||||||||||||||
| - рассмотреть следствия из теоремы о скалярном произведении в координатах -сформулировать свойства скалярного произведения векторов; -уметь находить угол между векторами; | |||||||||||||||||||||||||||||||||||
| Большинство учащихся будут уметь: | |||||||||||||||||||||||||||||||||||
| - правильно вычислять координаты векторов в прямоугольной системе координат. показать применение скалярного произведения векторов при решении задач; | |||||||||||||||||||||||||||||||||||
| Некоторые учащиеся смогут: | |||||||||||||||||||||||||||||||||||
| - анализирует главные составляющие темы, предлагает свои способы нахождения координат векторов в прямоугольной системе векторов. | |||||||||||||||||||||||||||||||||||
| Языковая цель | Учащиеся могут:
| ||||||||||||||||||||||||||||||||||
| Ключевые слова и фразы: Вектор-вектор- vector Направление – жолдау- direction | |||||||||||||||||||||||||||||||||||
| Оценивание | Формативное : лист оценивания | ||||||||||||||||||||||||||||||||||
| План 1.Организационный момент 2.Актуализация ЗУН 3.Изучение нового материала 4.Закрепление 5.Подведение итогов 6.Рефлексия 7.Постановка д/з | |||||||||||||||||||||||||||||||||||
| Планируемые сроки | Планируемые действия | Ресурсы | |||||||||||||||||||||||||||||||||
| Начало урока
| 1.Организационный момент
Приветствует учащихся, предлагает взять на выбор один листочек с «Корзины пожеланий».
1.Что такое вектор? 3. Чем характеризуется вектор? 4. По какой формуле вычисляется длина вектора? 5. Какие координаты имеет нулевой вектор? 6. Могут ли нулевые координаты быть у ненулевого вектора? - Какие вектора коллинеарные? - Какие вектора неколлинеарные? - Какие вектора соноправленные? - Какие противоположно направлены? 8. Какие действия вы умеете уже выполнять над векторами? 9. Что получается в результате этих операций? 10. Какую операцию еще не рассматривали? |
| |||||||||||||||||||||||||||||||||
| Середина урока | 4.Изучение нового материала
Деление на группы приемом «Атомы и молекулы» Прием «Мудрые совы» (работа в группах) Создать кластер по теме урока 1 группа : Скалярное произведение векторов 2 группа : угол между векторами Рассмотреть материал на стр.31 Даны координаты точек А (7;5); В (-6;2) С (3;-1). Найдите координаты следующих векторов: АВ + ВС. Подумайте, сколько решений имеет задача. Затем 1 паре оформить на плакате алгоритм решения, 2 паре само решение. Выбирает эксперта. Наблюдает, при необходимости корректирует решение ребят. Спикеры выполняют оценивание по критериям: Прежде чем определить скалярное произведение векторов, давайте построим угол между векторами. Пусть нам даны два ненулевых вектора Таким образом, углом между любыми двумя ненулевыми векторами Если же вектора параллельны или один из них равен нулю, то угол Рассмотрим примеры: Два вектора называются перпендикулярными, если угол между ними равен Скажите, глядя на рисунок, какие вектора будут перпендикулярными? Теперь, зная как определить угол между векторами, мы можем определить скалярное произведение векторов. Скалярным произведением векторов называется произведение их длин на косинус угла между ними : Запишите формулу в тетрадь и обведите в рамку. Таким образом, чтобы найти скалярное произведение нужно знать длины викторов и угол между ними. Пример: Дано: Найти: Решение: cos Обратите внимание, что в результете скалярного произведение обязательно будет число. Давайте теперь посмотрим какими свойствами обладает скалярное произведение. Запишите подзаголовок: свойства.
Это свойство вы докажете самостоятельно. Сколько утверждений будете доказывать. 2. 3. 4. 5. 6. 5.Закрепление Математический диктант (Работа в парах) Запомните пропуски, чтобы получить верное высказывание.
6. Найдите косинус угла между векторами 7. Вычислить скалярное произведение векторов
№68,69
| Листы А4 | |||||||||||||||||||||||||||||||||
| Конец урока | Подведение итогов «Сундук вопросов» Какие операции теперь мы можем выполнять над векторами? Скажите, что нужно знать для нахождения скалярного произведения? Чем отличаемся изученное действие от предыдущих? 7.Рефлексия Подведение итогов Прием «Железные цепи» Учащиеся подходят и берут друг друга за локти и говорят : сегодня на уроке мы… Я знаю, что ... Я хорошо знаю, что ... Я должен знать, что ... 8.Постановка д\з Стр.41 №70 | | |||||||||||||||||||||||||||||||||
Запомните пропуски, чтобы получить верное высказывание.
| Вариант I | Вариант II |
| 1. Если скалярное произведение двух векторов равно нулю, то эти векторы… | 1. Если два вектора перпендикулярны, то их скалярное произведение равно… |
| 2. Если A (5; 4; 0), B (3; –6; 2) – координаты концов отрезка AB, то его середина имеет координаты… | 2. Если A (4; –4; –2), B (–8; 4; 0) – координаты концов отрезка AB, то его середина имеет координаты… |
| 3. A (2; 7; 9), B (–2; 7; 1). Координаты вектора | 3. A (–3; 5; 5), B (3; –5; –2). Координаты вектора |
|
|
|
| дети выставляют оценки друг другу. |
|
Запомните пропуски, чтобы получить верное высказывание.
| Вариант I | Вариант II |
| 1. Если скалярное произведение двух векторов равно нулю, то эти векторы… | 1. Если два вектора перпендикулярны, то их скалярное произведение равно… |
| 2. Если A (5; 4; 0), B (3; –6; 2) – координаты концов отрезка AB, то его середина имеет координаты… | 2. Если A (4; –4; –2), B (–8; 4; 0) – координаты концов отрезка AB, то его середина имеет координаты… |
| 3. A (2; 7; 9), B (–2; 7; 1). Координаты вектора | 3. A (–3; 5; 5), B (3; –5; –2). Координаты вектора |
|
|
|
| дети выставляют оценки друг другу. |
|
| Вариант I | Вариант II |
| 1. Если скалярное произведение двух векторов равно нулю, то эти векторы… | 1. Если два вектора перпендикулярны, то их скалярное произведение равно… |
| 2. Если A (5; 4; 0), B (3; –6; 2) – координаты концов отрезка AB, то его середина имеет координаты… | 2. Если A (4; –4; –2), B (–8; 4; 0) – координаты концов отрезка AB, то его середина имеет координаты… |
| 3. A (2; 7; 9), B (–2; 7; 1). Координаты вектора | 3. A (–3; 5; 5), B (3; –5; –2). Координаты вектора |
|
|
|
| дети выставляют оценки друг другу. |
|
«Перепутанные логические цепочки»
| Координаты вектора a |
|
|
|
|
| a - b |
|
|
| ( |
| Координаты вектора АВ |
|
|
| ( |
| m (7; 5); n (- 6; 2) m+n |
|
«Перепутанные логические цепочки»
| Координаты вектора a |
|
|
|
|
| a - b |
|
|
| ( |
| Координаты вектора АВ |
|
|
| ( |
| m (7; 5); n (- 6; 2) m+n |
|
«Перепутанные логические цепочки»
| Координаты вектора a |
|
|
|
|
| a - b |
|
|
| ( |
| Координаты вектора АВ |
|
|
| ( |
| m (7; 5); n (- 6; 2) m+n |
|
«Перепутанные логические цепочки»
| Координаты вектора a |
|
|
|
|
| a - b |
|
|
| ( |
| Координаты вектора АВ |
|
|
| ( |
| m (7; 5); n (- 6; 2) m+n |
|
«Перепутанные логические цепочки»
| Координаты вектора a |
|
|
|
|
| a - b |
|
|
| ( |
| Координаты вектора АВ |
|
|
| ( |
| m (7; 5); n (- 6; 2) m+n |
|
«Перепутанные логические цепочки»
| Координаты вектора a |
|
|
|
|
| a - b |
|
|
| ( |
| Координаты вектора АВ |
|
|
| ( |
| m (7; 5); n (- 6; 2) m+n |
|
| Желаю получить пятёрку | удиви друзей своими ответами |
| пусть тебе повезёт | ты имеешь право на собственное мнение |
| хорошего настроения на уроке | стремись вперед, к чему-то новому |
| Пусть твой день будет насыщен яркими впечатлениями | Пусть твоя мечта осуществится |
|
|
|
|
|
|
«Перепутанные логические цепочки»
| Координаты вектора a |
|
| Длина вектора | ( |
| Коллинеарные вектора | Вектора,которые лежат на одной прямой |
| Соноправленные вектора | Вектора, которые направлены в одну сторону |
| Координаты вектора АВ |
|
| Координаты вектора a |
|
| Длина вектора | ( |
| Коллинеарные вектора | Вектора,которые лежат на одной прямой |
| Соноправленные вектора | Вектора, которые направлены в одну сторону |
| Координаты вектора АВ |
|
| Координаты вектора a |
|
| Длина вектора | ( |
| Коллинеарные вектора | Вектора,которые лежат на одной прямой |
| Соноправленные вектора | Вектора, которые направлены в одну сторону |
| Координаты вектора АВ |
|
| Координаты вектора a |
|
| Длина вектора | ( |
| Коллинеарные вектора | Вектора,которые лежат на одной прямой |
| Соноправленные вектора | Вектора, которые направлены в одну сторону |
| Координаты вектора АВ |
|
| Координаты вектора a |
|
| Длина вектора | ( |
| Коллинеарные вектора | Вектора,которые лежат на одной прямой |
| Соноправленные вектора | Вектора, которые направлены в одну сторону |
| Координаты вектора АВ |
|
| Координаты вектора a |
|
| Длина вектора | ( |
| Коллинеарные вектора | Вектора,которые лежат на одной прямой |
| Соноправленные вектора | Вектора, которые направлены в одну сторону |
| Координаты вектора АВ |
|
| Вариант I | Вариант II |
| 1. Если скалярное произведение двух векторов равно нулю, то эти векторы… | 1. Если два вектора перпендикулярны, то их скалярное произведение равно… |
| 2. Если A (5; 4; 0), B (3; –6; 2) – координаты концов отрезка AB, то его середина имеет координаты… | 2. Если A (4; –4; –2), B (–8; 4; 0) – координаты концов отрезка AB, то его середина имеет координаты… |
| 3. A (2; 7; 9), B (–2; 7; 1). Координаты вектора | 3. A (–3; 5; 5), B (3; –5; –2). Координаты вектора |
|
|
|
| дети выставляют оценки друг другу. |
|
| Вариант I | Вариант II |
| 1. Если скалярное произведение двух векторов равно нулю, то эти векторы… | 1. Если два вектора перпендикулярны, то их скалярное произведение равно… |
| 2. Если A (5; 4; 0), B (3; –6; 2) – координаты концов отрезка AB, то его середина имеет координаты… | 2. Если A (4; –4; –2), B (–8; 4; 0) – координаты концов отрезка AB, то его середина имеет координаты… |
| 3. A (2; 7; 9), B (–2; 7; 1). Координаты вектора | 3. A (–3; 5; 5), B (3; –5; –2). Координаты вектора |
|
|
|
| Координаты вектора a |
|
| Длина вектора | ( |
| Коллинеарные вектора | Вектора,которые лежат на одной прямой |
| Соноправленные вектора | Вектора, которые направлены в одну сторону |
| Координаты вектора АВ |
|

 Получите свидетельство
Получите свидетельство Вход
Вход



 )
)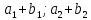 )
)








 Скалярное произведение векторов (298.3 KB)
Скалярное произведение векторов (298.3 KB)
 0
0 470
470 9
9 Нравится
0
Нравится
0