Юрченко Елена Александровна
учитель математики 9 класс, алгебра
Урок по теме: Системы уравнений с двумя переменными.
«Три пути ведут к знанию:
путь размышления – это путь самый благородный,
путь подражания – это путь самый легкий
и путь опыта – это путь самый горький».
Конфуций.
Цели урока
Обучающие: систематизировать знания по данной теме, выработать умение решать системы уравнений, содержащие уравнения второй степени графическим способом, способами подстановки и сложения.
Развивающие: развивать вычислительную технику, мыслительную активность, логическое мышление, интерес к предмету; способствовать формированию ключевых понятий; выполнение заданий различного уровня сложности.
Воспитывающие: воспитывать внимательность, аккуратность, умения четко организовывать самостоятельную и индивидуальную работу.
Оборудование: карточки – задания для индивидуальной работы, ,мультимедийный проектор.
Ход урока.
Организационный момент.
2. Фронтальный опрос (мозговой штурм) :
| Вопросы | Ответы |
| 1.Что называется решением уравнения с двумя переменными? | Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. |
| 2.Равносильные уравнения – это… | Это два уравнения с двумя переменными, имеющие одно и то же множество решений. |
| 3.Что мы называем графиком уравнения с двумя переменными? | Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство. |
| 4. Сколько пар решений может иметь система уравнений? | Одну. Две, несколько пар чисел. |
| 5. Назовите, что является графиком следующих функции? а) х² + у² = 9 б) х – 2у =8
в) ху = 6 д) х² + (у -1)²= 1 | а) окружность с центром (0;0) и r = 3. б) прямая у = 0,5х – 4.
в) - гипербола I и III четверти. д) окруж с центром (0;1) и r = 1. |
3. Индивидуальная работа с учащимися, имеющими слабую мотивацию к учебе.
Какие способы решения систем уравнений с двумя переменными вы знаете?
(Графический, подстановки, сложения) (
4. Презентации проектов учащихся по теме: “Различные способы решения систем уравнений”.
Каждое выступление ученика завершается обобщением представленного способа решения системы уравнений. Алгоритм решения выводится на экран и учитель с классом повторяет способ решения.
1. Способ подстановки.
1) Выразить из одного уравнения системы одну переменную через другую.
2) Полученное выражение подставить во второе уравнение системы.
3) Решить полученное уравнение с одной переменной.
4) Найти соответствующие значения второй переменной.
2. Способ сложения.
1) Домножить уравнения системы на такие числа, чтобы при сложении уравнений системы коэффициент перед одной из переменных стал равен нулю.
2) Сложить получившиеся уравнения.
3) Решить полученное в результате сложения уравнение с одной переменной.
4) Найти соответствующие значения второй переменной.
3. Графический способ.
1) Построить график каждого уравнения системы (в одной системе координат).
2) Найти значения координат точек пересечения построенных графиков.
3) Записать ответ : координаты точек пересечения графиков.
Ученики задают вопросы выступающим ученикам и учителю по домашней работе. Обсуждаются достоинства и недостатки каждого метода.
5. Рассмотрим подробно графический способ.
Как решается система графическим способом?
(Необходимо: построить графики уравнения в одной координатной плоскости; найти координаты точек пересечения графиков, которые и будут решением системы.)
Почему координаты точек пересечения являются решением системы уравнений?
(Координаты точек пересечения удовлетворяют каждому уравнению системы.)
Как записывается решение системы уравнений, если она решается графическим способом?
(Приближенным равенством для значений переменных.)
От чего зависит количество решений системы уравнений при графическом способе решения?
(От количества точек пересечения.)
Сколько точек имеют графики, если система имеет три решения? (Три точки.)
6. Работа с раздаточным материалом по карточкам.
Сколько точек пересечения имеют графики.
Сколько решений имеет система, (графики изображены на рисунке.)
Совместить графики уравнений с формулами, которыми они задаются.
7. Проверочная работа с использованием шаблонов координатной плоскости.
Изобразив схематически графики уравнений, укажите количество решений системы.
1 вариант . 2 вариант .
{ 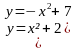 {
{ 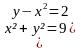
8. При графическом способе решения мы находим приближенные значения переменных. Как найти точные значения?
(Решить систему способом подстановки или сложения.)
Как решить систему способом подстановки?
(Выражают из уравнения одну переменную через другую. Подставляют эту подстановку в другое уравнение. Решают полученное уравнение с одной переменной. Находят соответствующие значение второй переменной, из подстановки).
Есть ли разница, из какого уравнения системы получить подстановку?
(Нет. Если в систему входит уравнение 1-ой степени, то подстановку получают из этого уравнения. Если оба уравнения второй степени, то подстановку получают из любого.)
Как записать решение системы? (Парой чисел.)
Как решить систему способом сложения?
9. .Устно
а) Определите степень уравнения : ху-2у=5 ; х+у=0; х²-у=2 ; х²+3у²=0 ; х+3у=4 .
Ответ: 2 ; 1; 2 ; 2 ; 1 .
б) Выразите одну переменную через другую.
4х-2у=6 Ответ: у=2х-3
ху=4 у=4:х
х+у=7 у=7-х
ху=5 у=5:х
3х-6у=9 у=0,5х-1,5у
10. Работа по учебнику : №442(б), 447(а), 450(а) ,451(г).
11. Из материалов ГИА : №1585,1594,1604.
12. Самостоятельная работа с последующей взаимопроверкой.
Решите систему уравнений:
1 вариант . 2 вариант.
{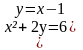 {
{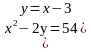
{ 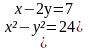 {
{ 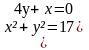
{  {
{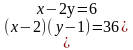
{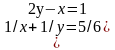 {
{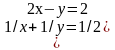
Дополнительное задание: имеет ли система уравнений решение ?
{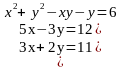
Ответ:
1 вариант 2 вариант
(-4;5);(2;1) (-6;-9);(8;5)
решений нет (4;-1);(-4;1)
(-0,5;-11);(8;6) (-4;-5);(14;4)
(-0,4;0,3);(3;2) . решений нет.
Дополнительное задание:(3;1).
13. Подведение итогов урока (ведет учитель математики).
Ученикам предлагается заполнить лист самоконтроля.
| Тема урока | Какие ключевые понятия повторили | Какие затруднения в работе вы испытывали и каковы причины | Личная оценка качества усвоения материала | Личная оценка активности и вклада в урок | Конструктивные предложения к уроку |
|
|
|
|
|
|
|
14.Домашнее задание : (дифференцированно)
1группа- №445(а), 448(б),451(а).
2группа- №453(а),456(б) ,458(а).
Литература:
Учебник для общеобразовательных школ “Алгебра 9 класс”, авторы: Г.В.Дорофеев , С.Б.Суворова, Москва, “Просвещение”, 2012.
Уроки алгебры в 9 классе, авторы В.И.Жохов, Л.Б.Крайнева,“Вербум-М”, 2000.
Дидактические материалы по алгебре 9 класс, авторы В.И.Жохов и др., “Просвещение”, 2012.
Открытый банк заданий по ГИА.
3000 задач с ответами по математике .И.В.Ященко и др., изд.Экзамен, Москва,2014.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Системы уравнений с двумя переменными (104 KB)
Системы уравнений с двумя переменными (104 KB)
 0
0 103
103 8
8 Нравится
0
Нравится
0


