Симметрия в пространстве.

Тема урока: «Теорема Виета» (Презентацию разработала Голенищева Зоя Тимофеевна, учитель математики МБОУ СОШ №19 г. Владивостока.)

Планируемые результаты

Предметные результаты:

1. Находить сумму и произведение корней приведенного квадратного уравнения.

2. Находить решения квадратных уравнений по теореме, обратной теореме Виета.

3. Составлять квадратные уравнения по теореме Виета.

Метапредметные результаты:

1. Исследовать и устанавливать связь между понятиями, данными в уроке.

2. Выдвигать гипотезы о зависимостях и проводить обобщение между понятиями.

Личностные результаты:

1. Формировать коммуникативные компетенции и творческие способности обучающихся.

2. Развивать интерес к предмету, используя исторические факты, как к математической науке.

План урока:

• Проверка выполнения домашней работы
• Повторение изученного материала
• Исследовательская работа
• Теорема Виета
• Закрепление знаний
• Самостоятельная работа
• Итог урока

Проверка домашней работы

Решить уравнения

5х 2 = 9х + 2

5х 2 – 9х – 2 = 0

Ответ: - 0,2; 2

3х 2 – 14 х +16=0

Ответ: 2, 2 .

18 + 3х 2 – х = 0

3х 2 – х + 18 = 0

Ответ: нет корней.

2х 2 + 3х = 0

х (2х + 3) = 0

Ответ: - 1,5; 0.

– х 2 + 4 = 0

х 2 = 4

Ответ: - 2; 2.

Повторение изученного

• Какое уравнение называется квадратным?
• Какой общий вид имеет квадратное уравнение?

а) ах² + с = 0; б) ах² + b х+с=0; в) х² + b х+с=0.

• Какое уравнение называется неполным? Какое приведённым?
• Что называют дискриминантом квадратного уравнения?
• Назовите формулу корней квадратного уравнения.
• Сколько корней может иметь квадратное уравнение?
• От чего зависит количество корней квадратного уравнения?

«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.

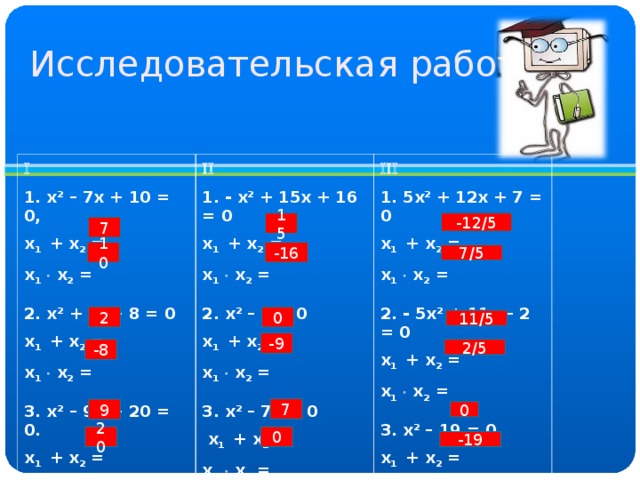
Исследовательская работа



1. х 2 – 7х + 10 = 0,

х 1 + х 2 =

х 1  х 2 =

2. х 2 + 2х – 8 = 0

х 1 + х 2 =

х 1  х 2 =

3. х 2 – 9х + 20 = 0.

х 1 + х 2 =

х 1  х 2 =



1. - х 2 + 15х + 16 = 0

х 1 + х 2 =

х 1  х 2 =

2. х 2 – 9 = 0

х 1 + х 2 =

х 1  х 2 =

3. х 2 – 7х = 0

х 1 + х 2 =

х 1  х 2 =



1. 5х 2 + 12х + 7 = 0

х 1 + х 2 =

х 1  х 2 =

2. - 5х 2 + 11х – 2 = 0

х 1 + х 2 =

х 1  х 2 =

3. х 2 – 19 = 0

х 1 + х 2 =

х 1  х 2 =

-12 / 5

15

7

10

-16

7 /5

2

0

11/5

-9

2/5

-8

7

9

0

20

0

-19

Теорема Виета

Сумма корней приведённого квадратного уравнения

равна второму коэффициенту,

взятому с противоположным знаком,

а произведение корней равно свободному члену.

Теорема Виета

• Пусть х 1 и х 2 корни уравнения

• Пусть х 1 и х 2 корни уравнения

х 2 + рх + q = 0,

ах 2 + вх + с = 0,

тогда:

• х 1 + х 2 = - в : а,
• х 1 ∙ х 2 = с : а

тогда:

• х 1 + х 2 = -р,
• х 1 ∙ х 2 = q

Теорема , обратная теореме Виета

• Пусть х 2 + рх + q = 0,
• х 1 + х 2 = -р,
• х 1 ∙ х 2 = q

• Пусть ах 2 + вх + с = 0,
• х 1 + х 2 = - в : а,
• х 1 ∙ х 2 = с : а

тогда:

тогда:

х 1 и х 2 корни уравнения

• х 1 и х 2 корни уравнения

В 1591 г. Ф. Виет вывел формулы, выражающие зависимость корней квадратного уравнения от его коэффициентов и сформулировал свою знаменитую теорему

Именно с 1591 г. мы пользуемся формулами при решении квадратных уравнений.

Теорема Виета

Поэтом по праву должна быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого –

Умножишь ты корни – и дробь уж готова:

В числителе с , в знаменателе а .

И сумма корней тоже дроби равна,

Хоть с минусом дробь та, что за беда:

В числителе - в , в знаменателе – а .

не используя формулу корней, найдите корни квадратного уравнения:

• х 2 + 3х + 2 = 0
• х 2 - 15х + 14 = 0
• х 2 + 3х - 4 = 0
• х 2 - 10х - 11 = 0
• х 2 + 9х + 20 = 0
• х 2 - 15х + 36 = 0
• х 2 + 5х - 14 = 0

• х 1 = - 2, х 2 = - 1
• х 1 = 14, х 2 = 1
• х 1 = -4, х 2 = 1
• х 1 = 11, х 2 = -1
• х 1 = -5, х 2 = -4
• х 1 = 12, х 2 = 3
• х 1 = 2, х 2 = -7

Составьте квадратное уравнение, если его корни равны

• х 1 = -3, х 2 = 1
• х 1 = -3, х 2 = -4
• х 1 = 5, х 2 = 6
• х 1 = 4, х 2 = 2
• х 1 = 3, х 2 = -5

• х 2 +2х – 3 = 0
• х 2 +7х + 12 = 0
• х 2 - 11х + 30 = 0
• х 2 - 6х + 8 = 0
• х 2 +2х – 15 = 0

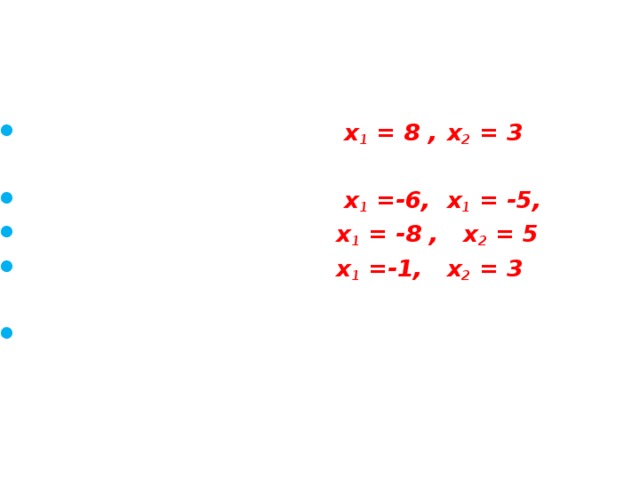
правильно ли найдены корни уравнения?

• х 2 – 11х + 24 = 0 х 1 = 8 , х 2 = 3
• х 2 + 11х + 30 = 0 х 1 = -6, х 1 = -5,
• х 2 + 3х - 40 = 0 х 1 = -8 , х 2 = 5
• х 2 – 2х - 3 = 0 х 1 =-1, х 2 = 3
• Сравните корни и свободный член уравнения.

Вывод:

• Если свободный член уравнения – отрицательное число , то корни различные по знаку;
• если свободный член уравнений – положительное число , то оба корня имеют одинаковые знаки .

в первый столбик выпишите уравнения, одним из корней которых будет 1, а в другой столбик – одним из корней будет - 1.

• х 2 - 15х + 14 = 0
• х 2 + 9х + 10 = 0
• х 2 + 3х - 4 = 0
• х 2 + 3х + 2 = 0
• х 2 + 5х - 14 = 0
• х 2 - 9х - 10 = 0
• х 2 + 8х - 9 = 0
• х 2 - 15х + 36 = 0
• х 2 + 8х + 7 = 0

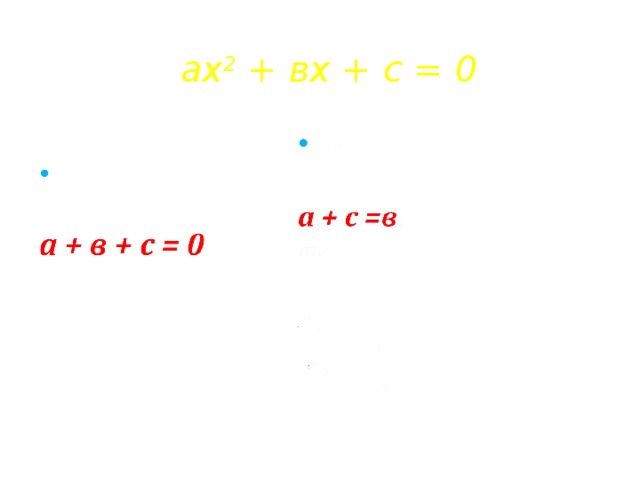
ах 2 + вх + с = 0

Проверьте, справедливо ли данное утверждение для неприведенных квадратных уравнений. Решите уравнения.

Самостоятельная работа

Найдите подбором корни квадратного уравнения:

х 2 – 17х + 42 = 0

х 2 + 8х + 15 = 0

х 2 – 11х – 80 = 0

Один из корней квадратного уравнения равен – 3. Найдите второй корень и неизвестный коэффициент.

х 2 – 5х + q = 0

х 2 + p х + 18 = 0

Проверим работу

6-7 баллов – «5»

5-4 балла – «4»

2-3 балла - «3»

0-1 балла – «2».

Найдите подбором корни

квадратного уравнения:

1.х 2 – 17х + 42 = 0 (1 б)

х 1 = 4; х 2 = 13

2. х 2 + 8х + 15 = 0 (1 б)

х 1 = - 3 ; х 2 = -5

3. х 2 – 11х – 80 = 0 (1 б)

х 1 = - 5 ; х 2 = 16

Один из корней квадратного уравнения равен – 3. Найдите второй корень и неизвестный коэффициент.

х 2 – 5х + q = 0 (2 б)

х 2 + p х + 18 = 0 (2 б)

1. х 2 = 8; q = - 24

2. х 2 = - 6; q = 9

Решение квадратных уравнений методом «переброски» старшего коэффициента

х 3

По теореме, обратной теореме Виета

Решение квадратных уравнений методом «переброски» старшего коэффициента

или

корень квадратного уравнения можно найти по свойству коэффициентов

Решить уравнения

Для тех, кто хочет знать больше.

На уроке «Я узнал …» «Я научился …» «Я могу …»

Задание на дом

п. 20, № 561 (а, б), № 563 (в, г)

Написать синквейн по теме урока: «Теорема Виета».

Напишите телеграмму из 6, 7 слов

по поводу урока, трудностей, успехов.

.

Используемая литература:

• «Алгебра 8 класс» Ю.Н. Макарычева и др.; под редакцией С.А. Теляковского.
• «Тематический сборник тестовых заданий по алгебре для подготовки к государственной (итоговой) аттестации в новой форме», базовый уровень, под редакцией Е.А. Семенко, Просвещение-Юг, Краснодар, 2008 г.
• «Экзаменационные тестовые задания», Федеральная служба по надзору в сфере образования и науки РФ, 2008 г.
• «Краевые диагностические работы по алгебре в 9 классе», Департамент образования и науки Краснодарского края, ККИДППО, 2008 г.
• Выполнила: Голенищева Зоя Тимофеевна
• МБОУ СОШ №19 г. Владивостока .